What is the Most Triangular Country?
Summary
A list of 196 countries ordered by “triangularity” can be found in the Results section of this post.
Details of the methods are described in the following two sections. I have included all my code at the very end of this post.
I was inspired to write this blog post after reading two excellent posts. One of these is about finding the most rectangular country and is by David Barry. The other is by Gonzalo Ciruelos and is about finding the roundest country. I’ll provide links to these posts below:
I thought it would be interesting to have a go at calculating the most triangular country. I followed a similar method to the previous posts. The first step is to define mathematically what “triangularity” means. The next step is to find a way to calculate triangularity for every country in the world.
In summary, the method involves picking a similarity measure between a triangle and a country, then, for each country, finding the triangle that maximises the similarity measure. This maximum similarity is the country’s triangularity. Finding a triangle that maximises similarity is an optimisation problem. A triangle can be uniquely defined by the coordinates of its three vertices. Hence, there are 6 free parameters in the optimisation problem (an \(x\) and \(y\) coordinate per vertex). In contrast, defining a rectangle requires five parameters, and a circle requires only three (e.g. the coordinates of the center of the circle and its radius). As a result of the greater number of free parameters, this optimisation is more prone to get stuck in local optima. I tackled the problem by running the optimisation multiple times per country with randomised initial conditions.
Overall, I am happy with the results.
Theory
Following Gonzalo Ciruelos’ example, I will define the similarity of two sets \(A\) and \(B\) in \(\mathbb{R}^{2}\) as the area of the intersection of the sets divided by the maximum of the areas of the sets.
\[\textrm{similarity} (A,B) = \frac{\textrm{area}( A \cap B)}{\max \{ \textrm{area} {(A)},\textrm{area} (B) \} }\]This definition of similarity has the following properties:
-
Because area is never negative, \(\textrm{similarity}(A,B) \geq 0\).
-
Because \(\textrm{area}(A \cap B) \leq \max \{\textrm{area}(A), \textrm{area}(B)\}\), \(\textrm{similarity} (A,B) \leq 1\).
-
If \(A=B\), then \(\textrm{similarity} (A,B) = 1\).
-
If \(A \cap B = \emptyset\), then \(\textrm{similarity} (A,B) = 0\).
Let the country \(C\) be a set in the plane, \(C \subset \mathbb{R}^{2}\). Let \(T(\textbf{x},\textbf{y})\) be a set in the plane, \(T(\textbf{x},\textbf{y}) \subset \mathbb{R}^{2}\), that is enclosed by the triangle with vertices: \((x_{1},y_{1})\), \((x_{2},y_{2})\), \((x_{3},y_{3})\).
Then, the triangularity of \(C\) is the maximum similarity between \(C\) and some \(T(\textbf{x},\textbf{y})\):
\[\textrm{triangularity} (C) = \max_{\textbf{x},\textbf{y}} \textrm{similarity} (C,T(\textbf{x},\textbf{y}))\]where
\[\textbf{x} = [x_{1},x_{2},x_{3}]\] \[x_{i} \in \mathbb{R}\] \[\textbf{y} = [y_{1},y_{2},y_{3}]\] \[y_{i} \in \mathbb{R}\]We have that
- For any triangle \(T\), \(\textrm{triangularity} (T) = 1\).
In practice, calculating the triangularity exactly for a country is not possible. However, using optimisation methods, it is possible to produce a reasonable approximation.
Method
I used the freely available countries dataset from Natural Earth. The shapefile contains an ordered list of latitude and longitude points for the borders of 247 countries. Countries have one or more continuous parts (for example, each part might be an island belonging to the country). The part information is a series of indices that mark where the points for each part of the country begin and end.
The first step in processing the data from the shapefiles was to convert the latitude and longitude coordinates using an azimuthal projection centered on each country. To do the conversion, I adapted some code from this blog post. Then, using the python Shapely package, I converted the coordinates into a set of polygons for each country.
I wrote a function to calculate the similarity between the set of polygons that make up a country and a given triangle, making heavy use of the intersection and area methods from the Shapely package. I created an R-Tree for each country, using the STRtree class in Shapely. This makes it fast to query which parts of the country might intersect with the triangle. Then, for each of these parts, I calculated the area of intersection with the triangle. These are summed and divided by the maximum of the total area of the country and the area of the triangle, as per the definition of similarity. This worked for all countries, apart from Antarctica, due to a problem with the polygon intersecting with itself.
To find the triangle that maximised the triangularity of each country, I began with an initial guess: three random points on the country’s border. I then used the minimize function in scipy, using the Nelder-Mead simplex method, to find a triangle that maximised the triangularity of the country, i.e. minimising the cost function:
\[f(\textbf{x},\textbf{y}) = 1 - \textrm{similarity} (C,T(\textbf{x},\textbf{y}))\]Interestingly, for a given country, the resulting triangles (and triangularities) after the optimisation varied quite significantly, depending on the initial guess. The problem is that the optimisation gets stuck in a local minimum of the cost function. In order to try and avoid local minima, I ran the optimisation routine 20 times for each country with a different initial guess each time, and used the estimate of triangularity from the best run. This is still no guarantee that local minima will be avoided, but does certainly help.
The final step was simply to save an image of each country and its most similar triangle, and create a CSV file with estimated triangularity for each country.
Results
The results shown here are all the countries in the Natural Earth dataset that are also countries according to Encyclopedia Britannica. This means a slightly thinned down list of 196 countries from the original list of 247.
So these results would suggest that the most triangular country in the world is Nicaragua, followed closely by Bosnia and Herzegovina. (I will add that I found out an interesting fact about the flag of Bosnia and Herzegovina which is that it features a triangle that, according to Wikipedia, represents the approximate shape of the territory. Indeed, it does!)
I plotted the triangularity of each country by rank, labelling every 25th country. This shows that there is a quite gentle decrease in triangularity for the first 150 countries followed by a sharp drop off, seemingly due to countries that have multiple parts. The least triangular country is the Marshall Islands, hardly surprising considering the country is a collection of tiny islands spread over a large area of ocean. The least triangular country that isn’t a group of islands is Vietnam.
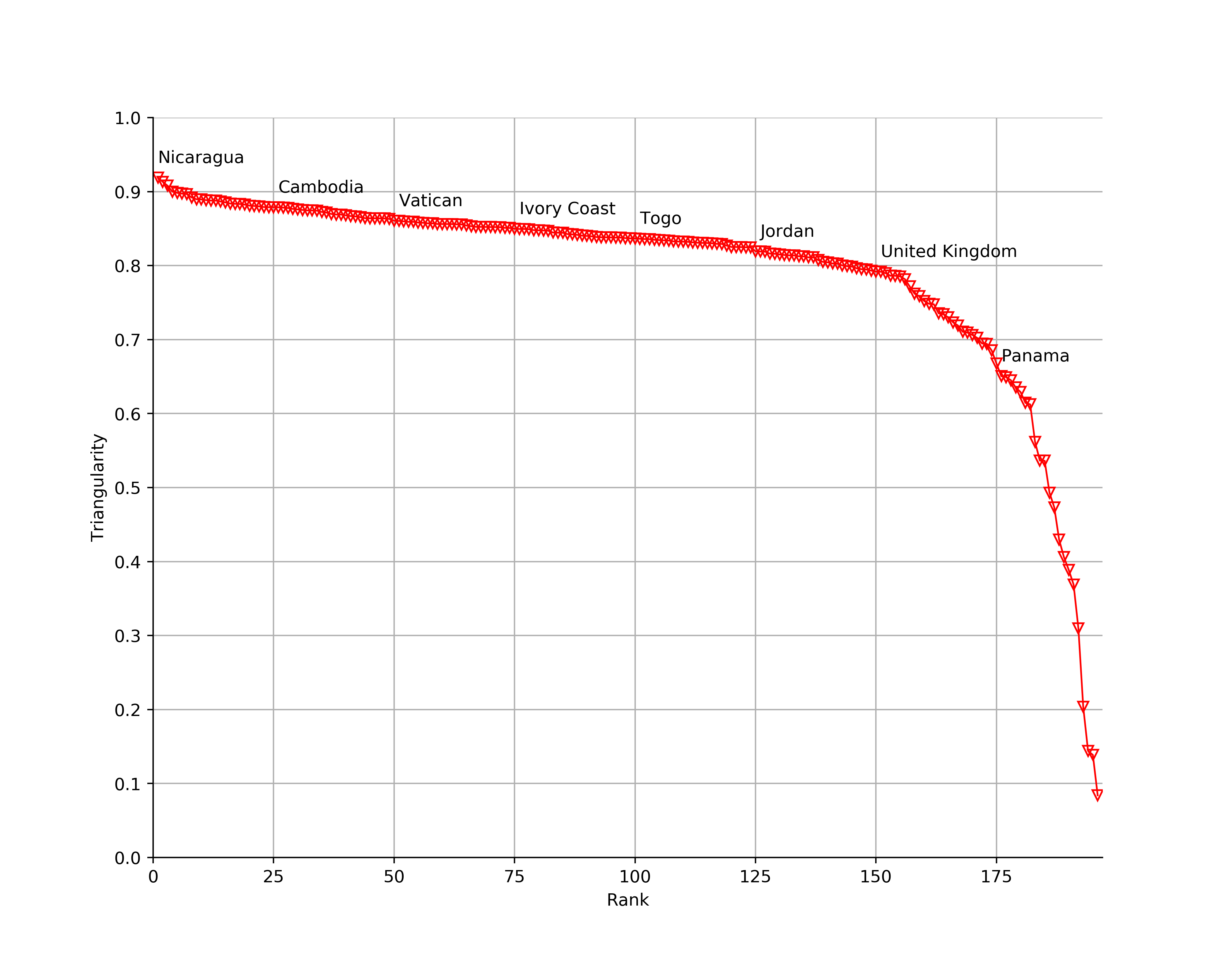
Looking at pictures of the best triangles, it does seem like the optimisation has worked as intended, at least to the human eye. I think I would have picked similar triangles if I were doing the process manually.
Below is the final list of triangular countries. If you want to view the images in more detail, you can either open the images in a new tab or download them.
| Rank | Country | Triangularity | Image |
|---|---|---|---|
| 1 | Nicaragua | 0.918672 | 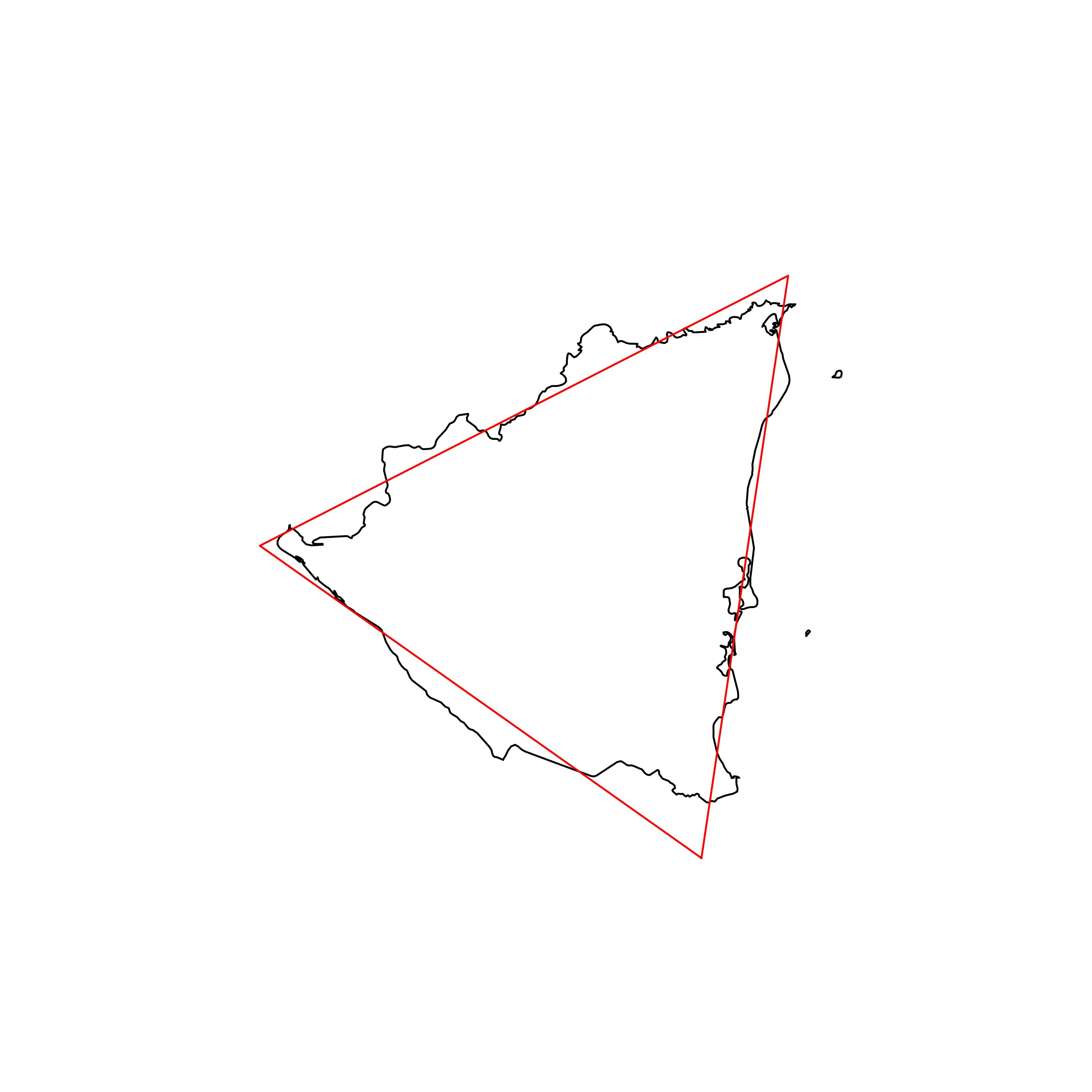 |
| 2 | Bosnia and Herzegovina | 0.913202 | 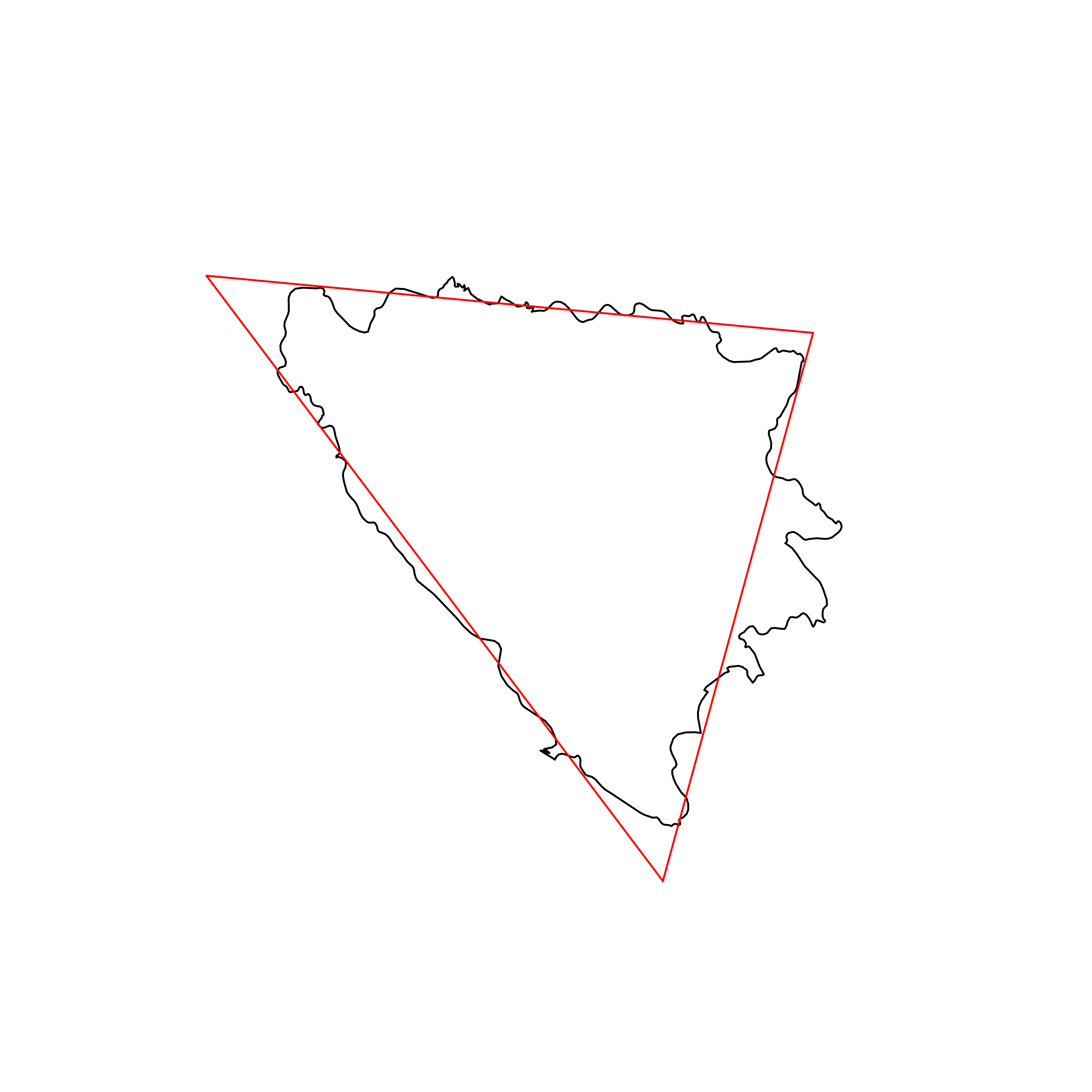 |
| 3 | Namibia | 0.907920 | 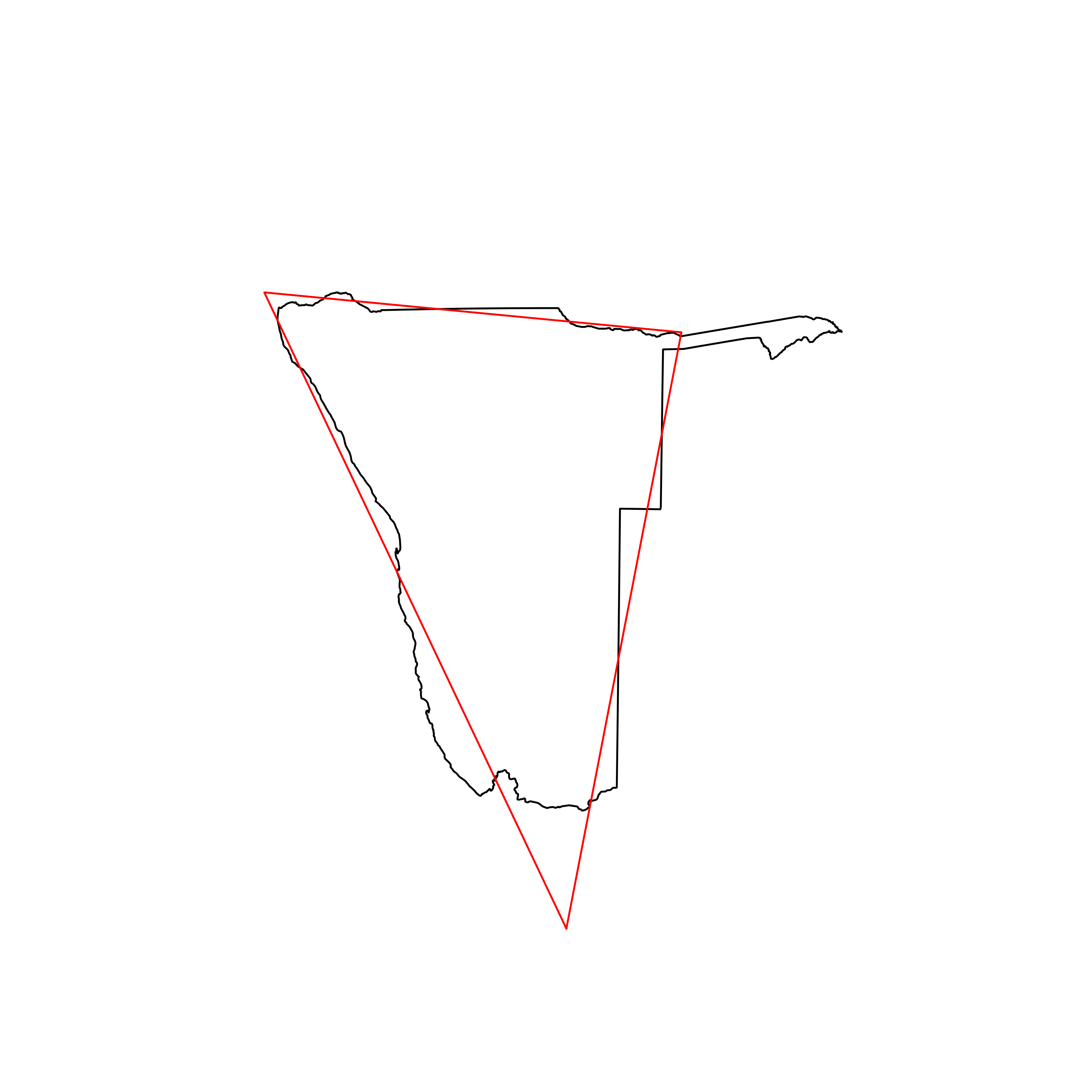 |
| 4 | Mauritania | 0.899915 | 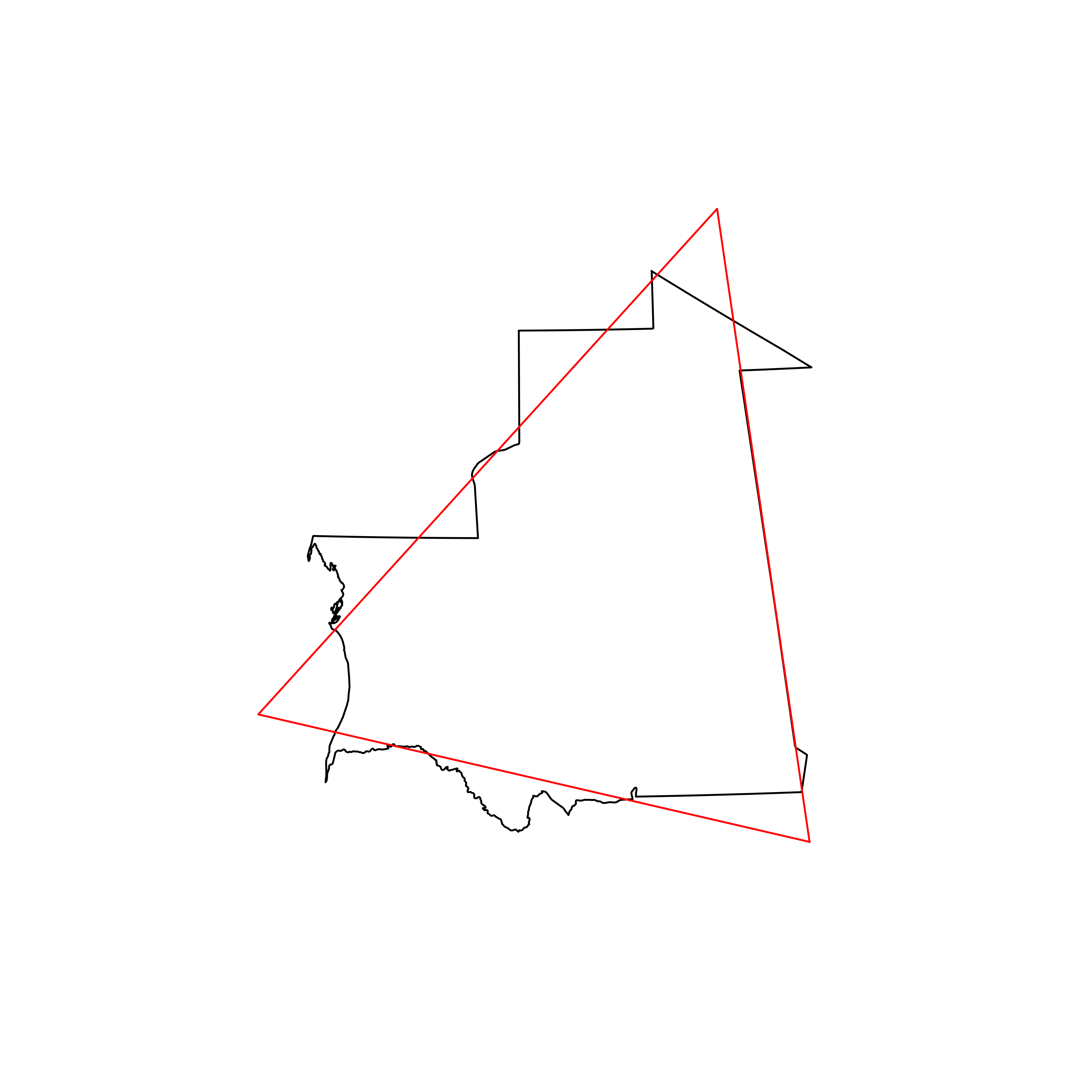 |
| 5 | Bolivia | 0.898253 | 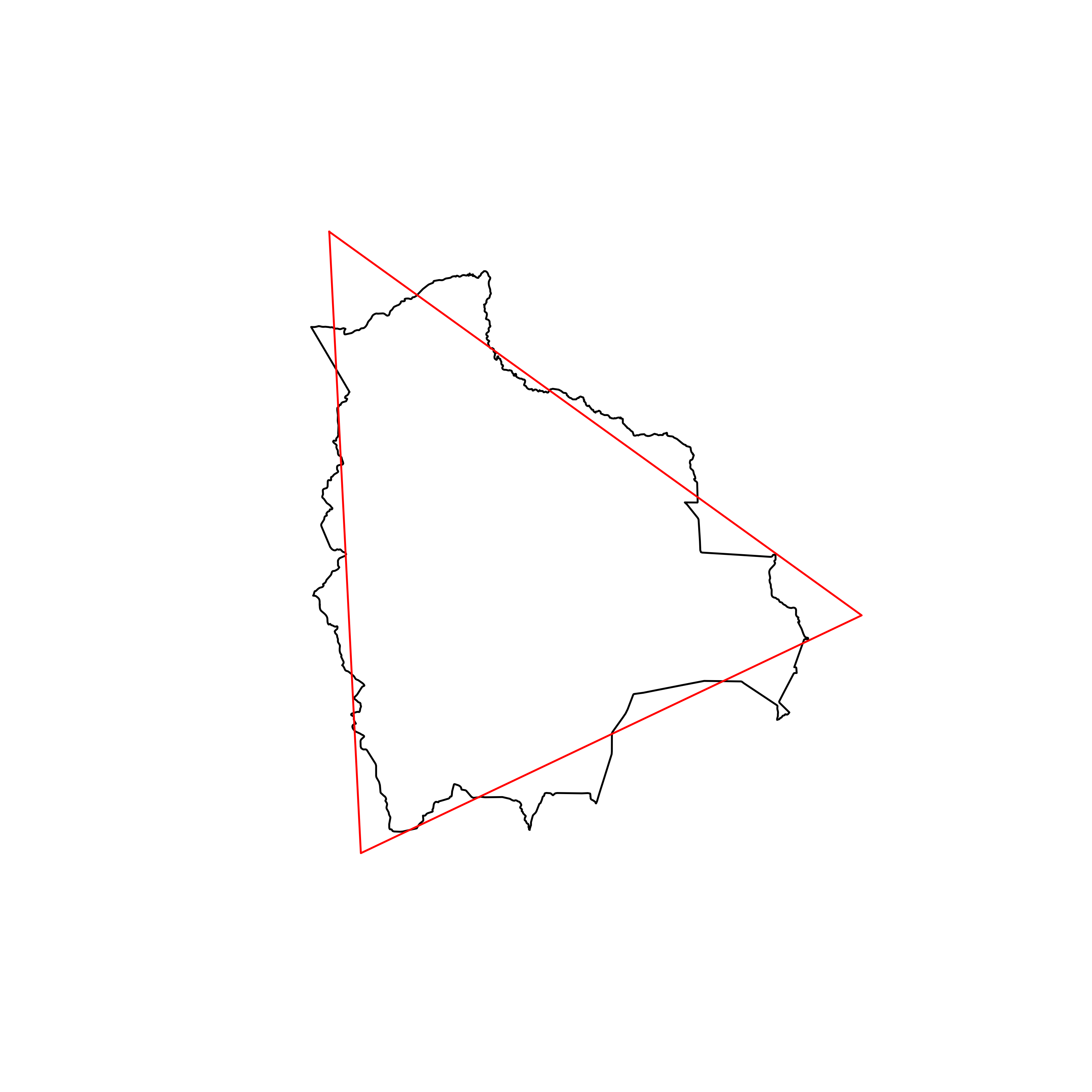 |
| 6 | Bhutan | 0.897231 | 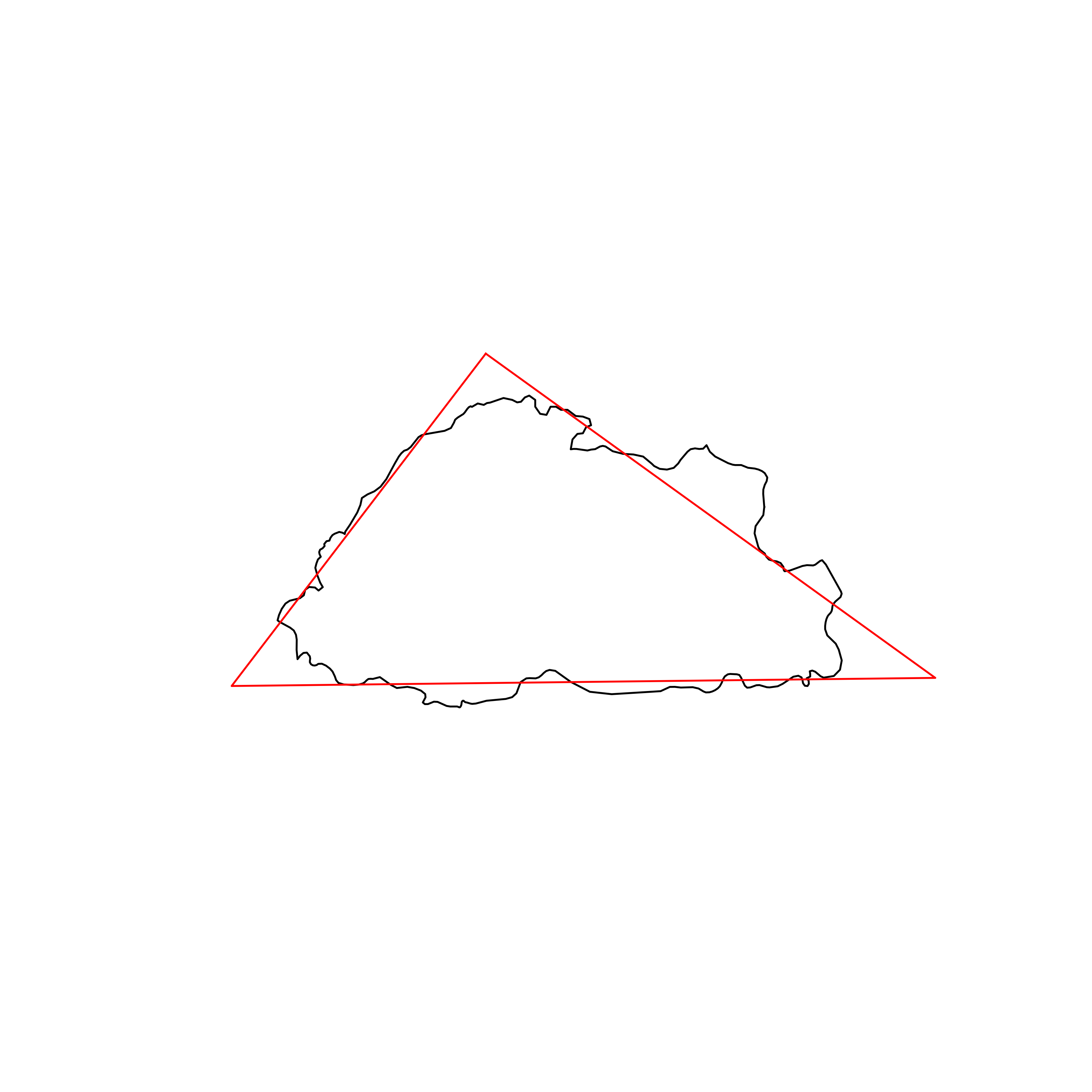 |
| 7 | Sri Lanka | 0.896619 | 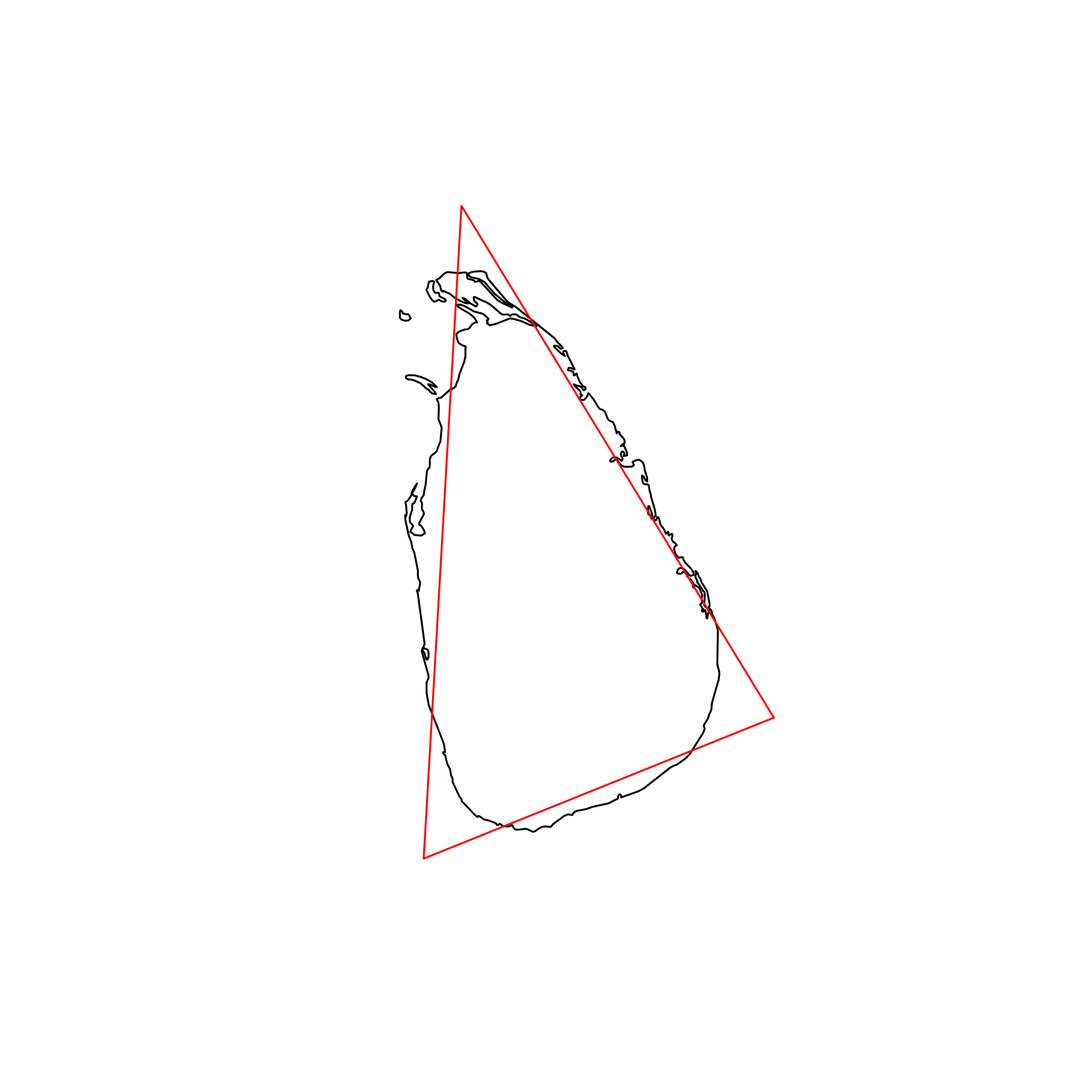 |
| 8 | Barbados | 0.892064 | 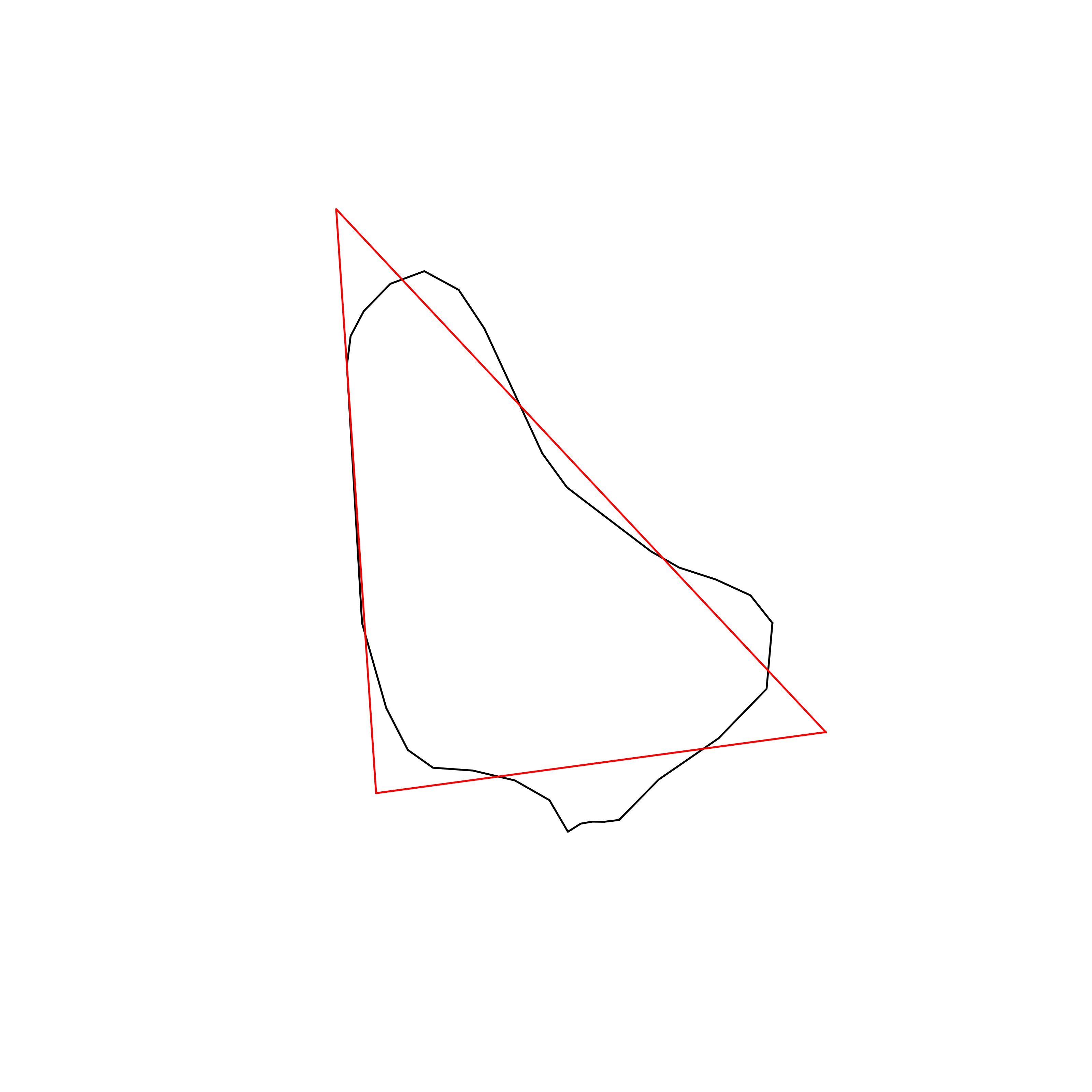 |
| 9 | Botswana | 0.889655 | 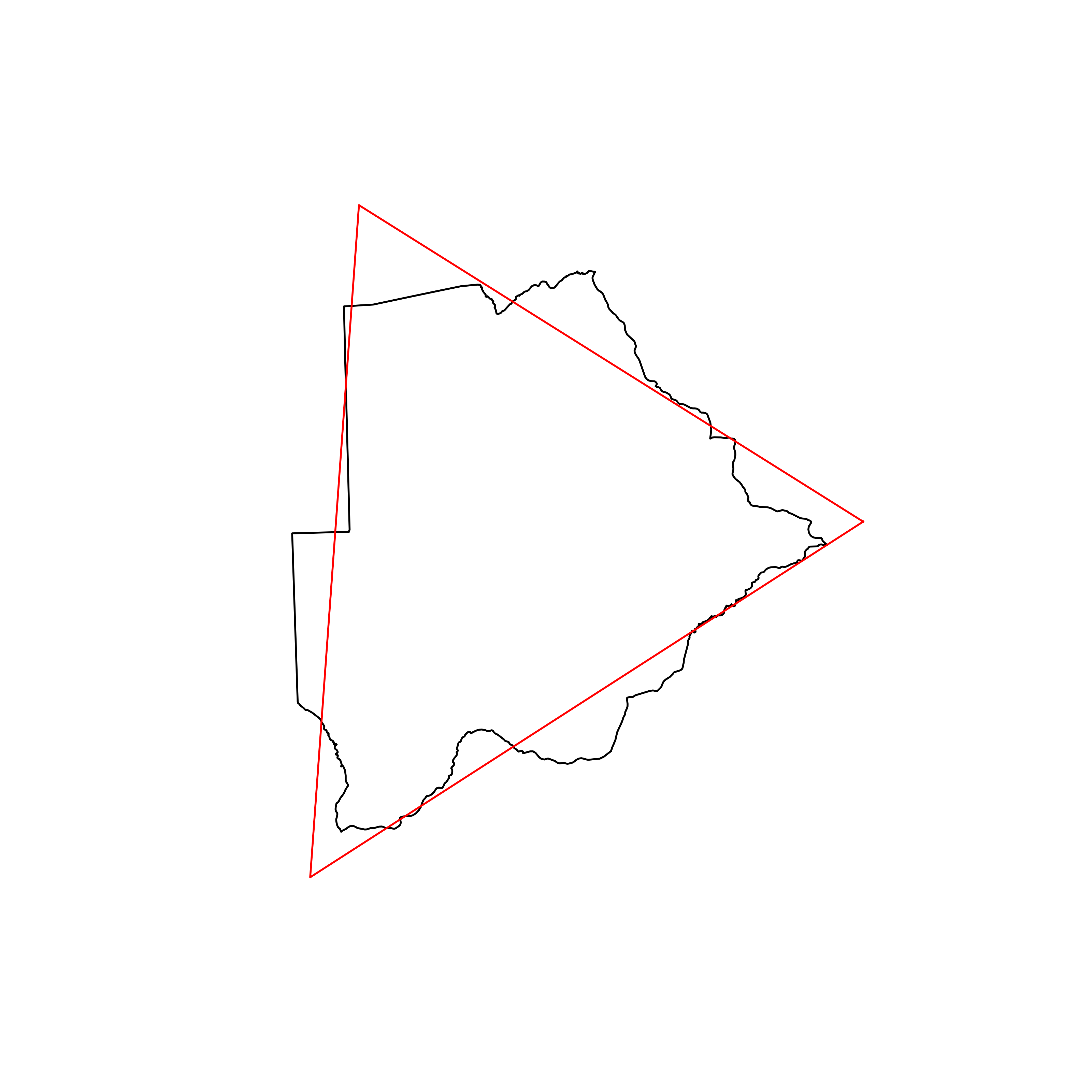 |
| 10 | Dominican Republic | 0.889356 | 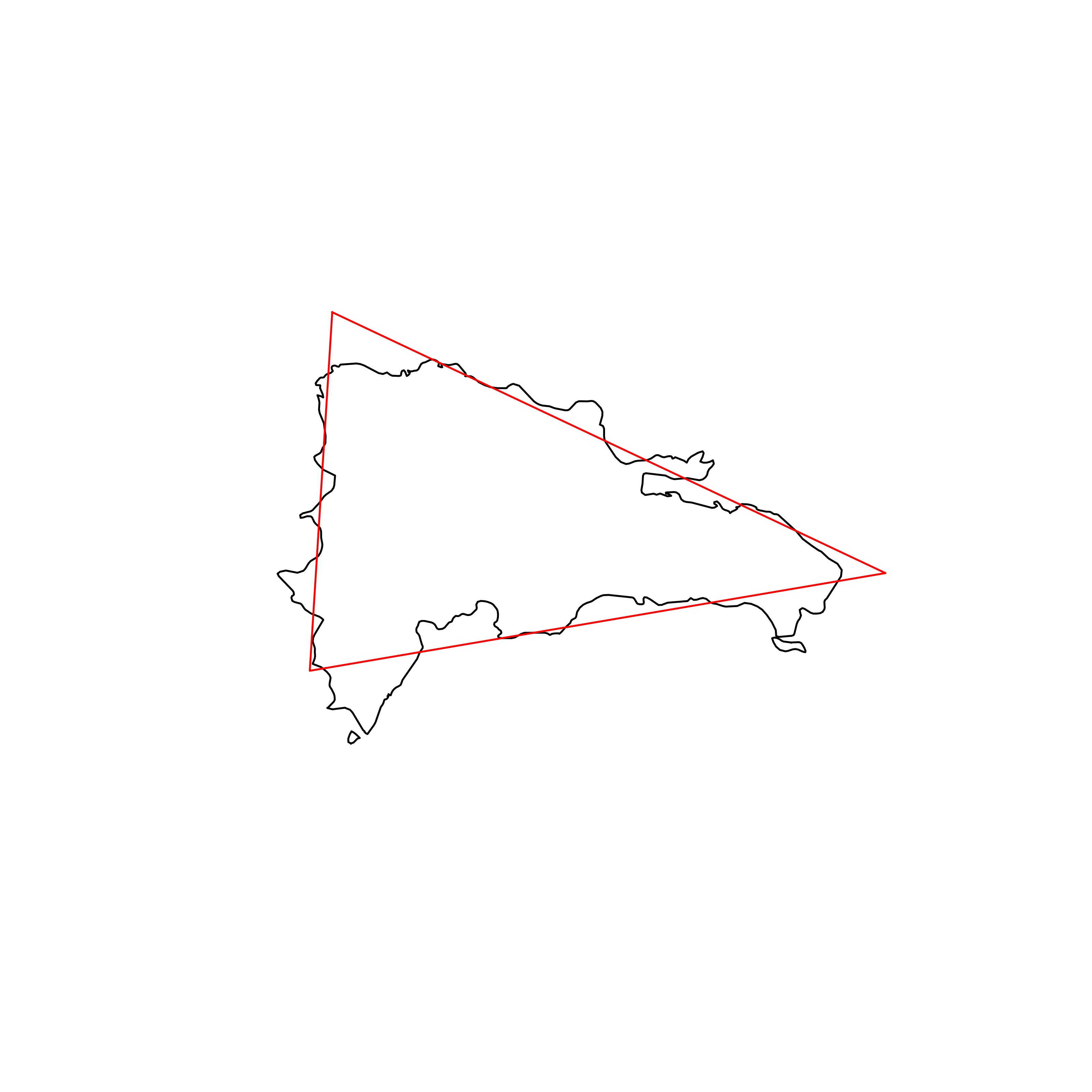 |
| 11 | Argentina | 0.888404 | 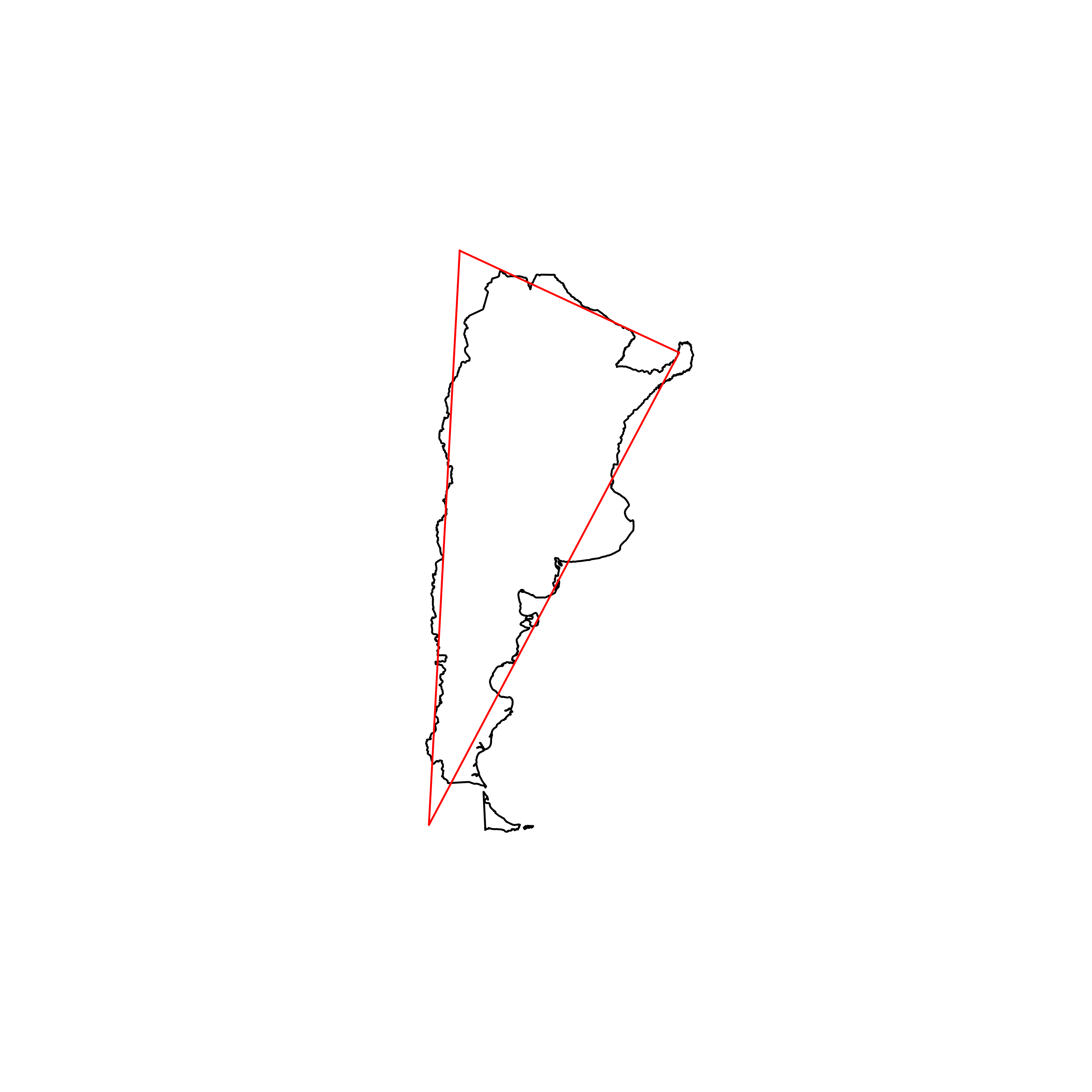 |
| 12 | Algeria | 0.887851 | 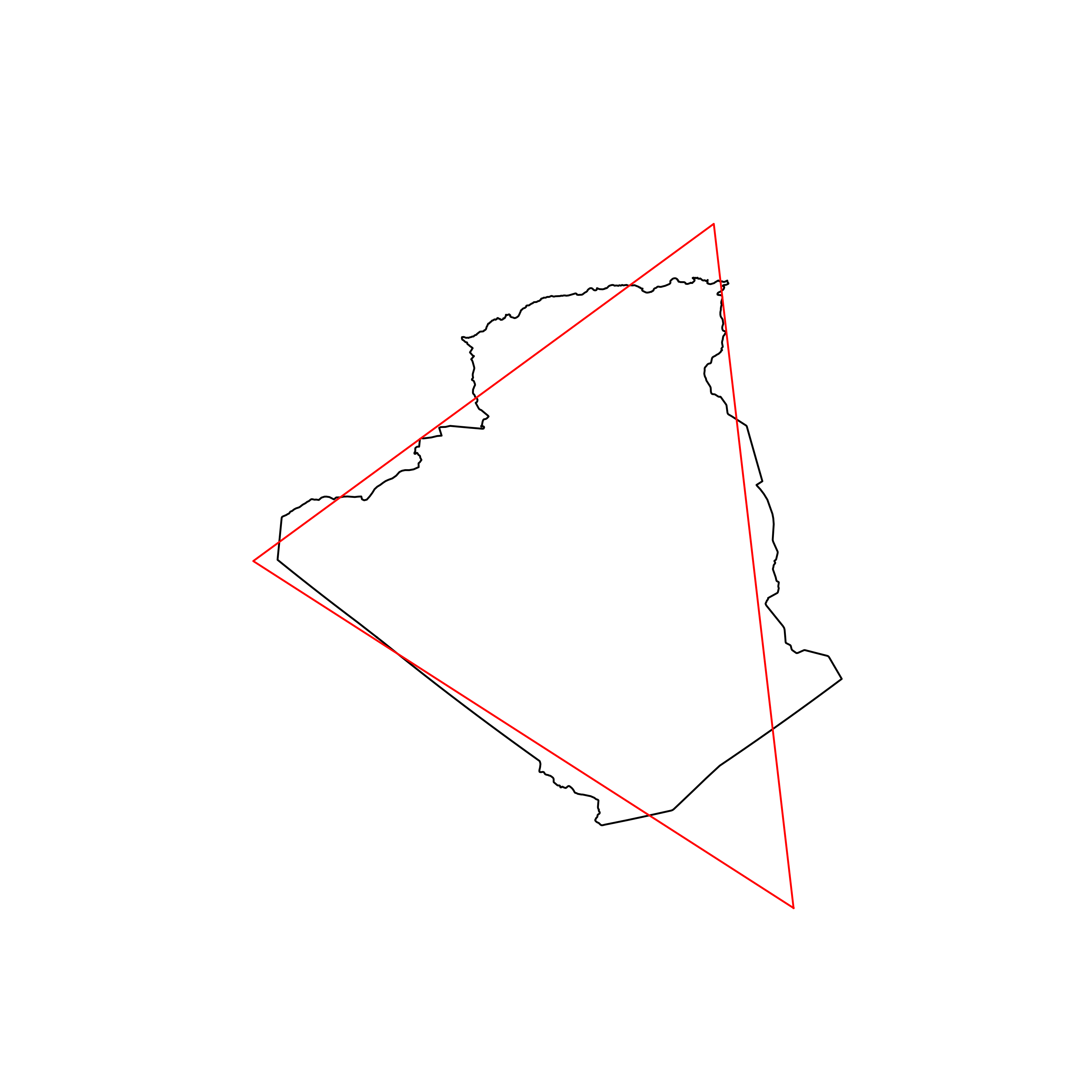 |
| 13 | Andorra | 0.887847 | 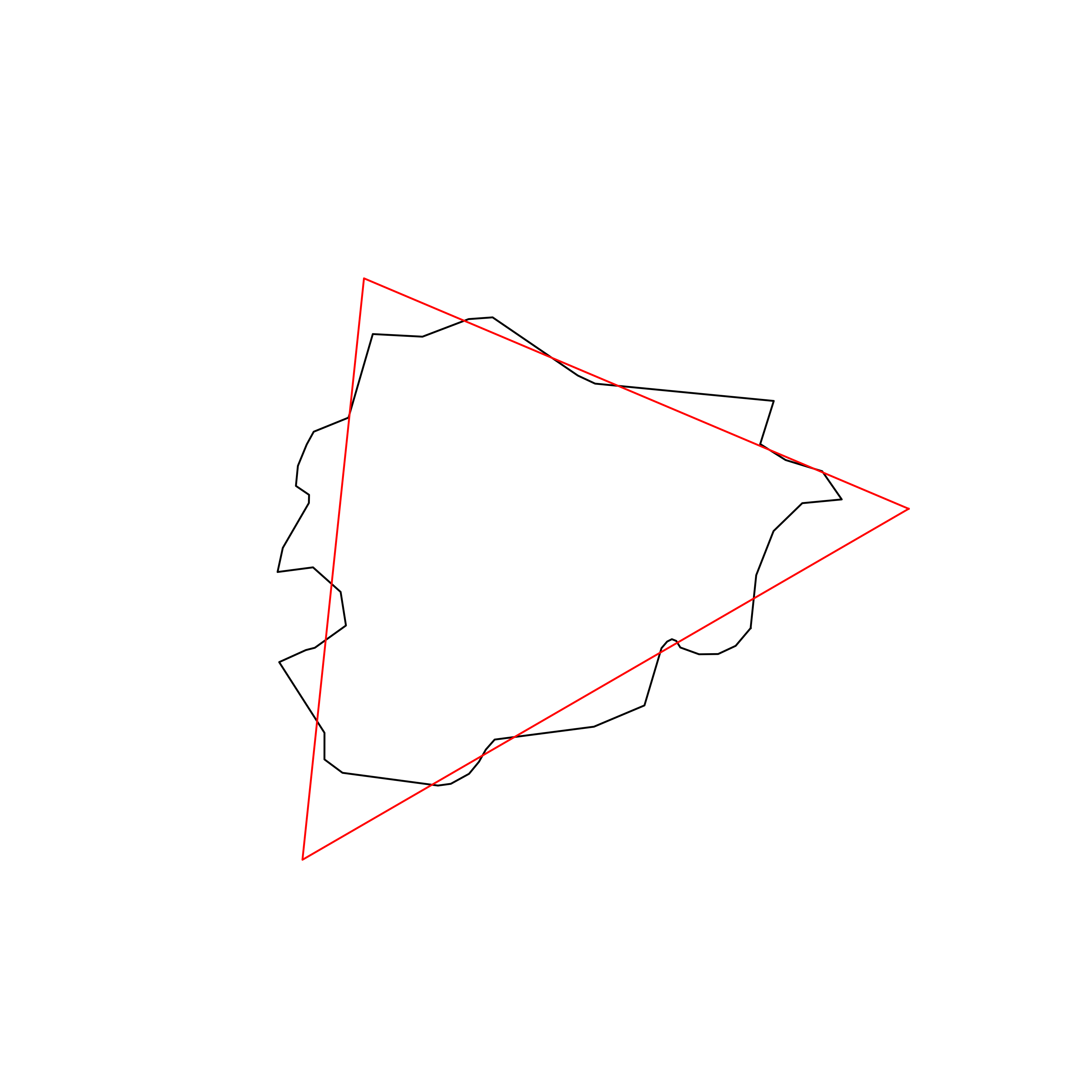 |
| 14 | Belarus | 0.886588 | 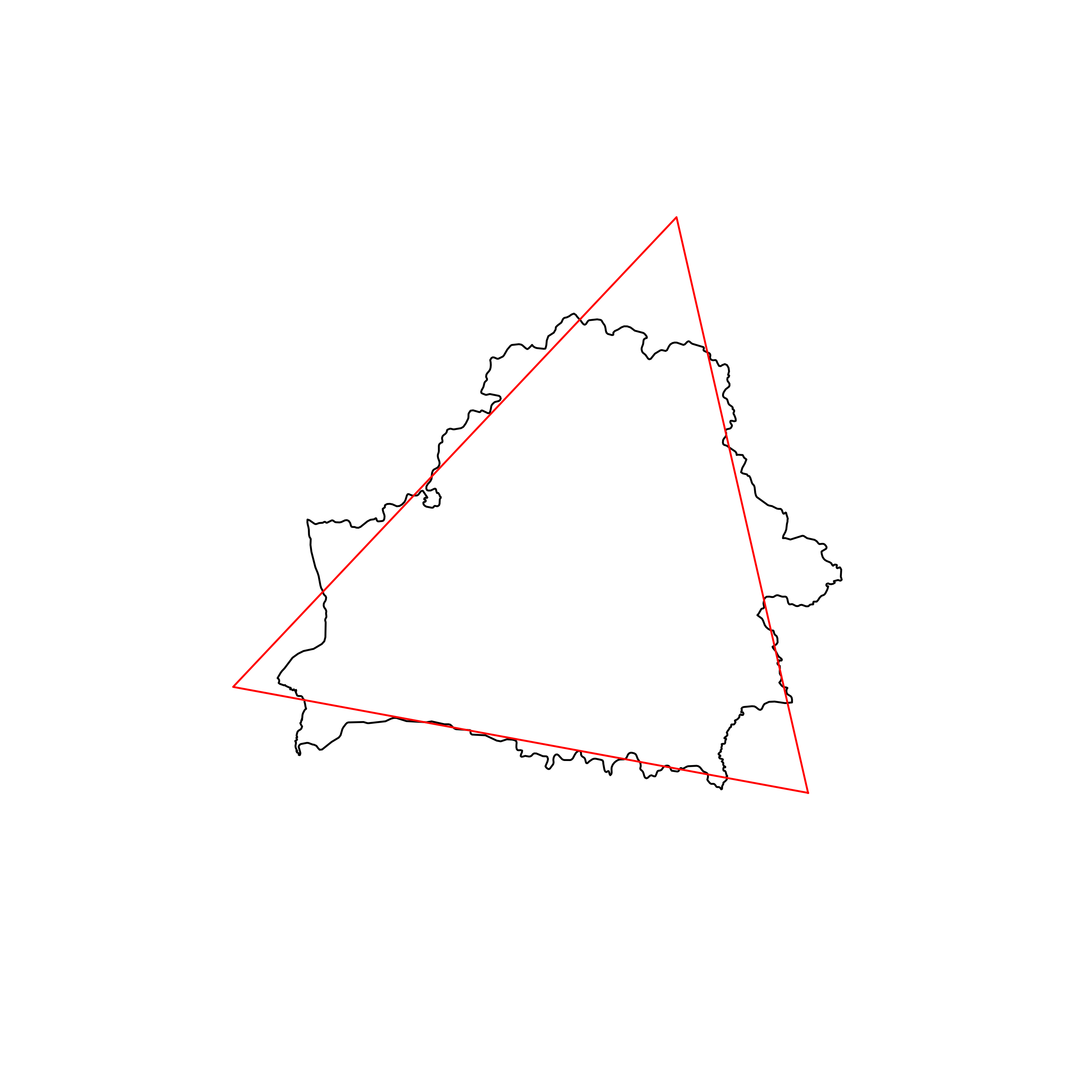 |
| 15 | Saint Lucia | 0.885393 | 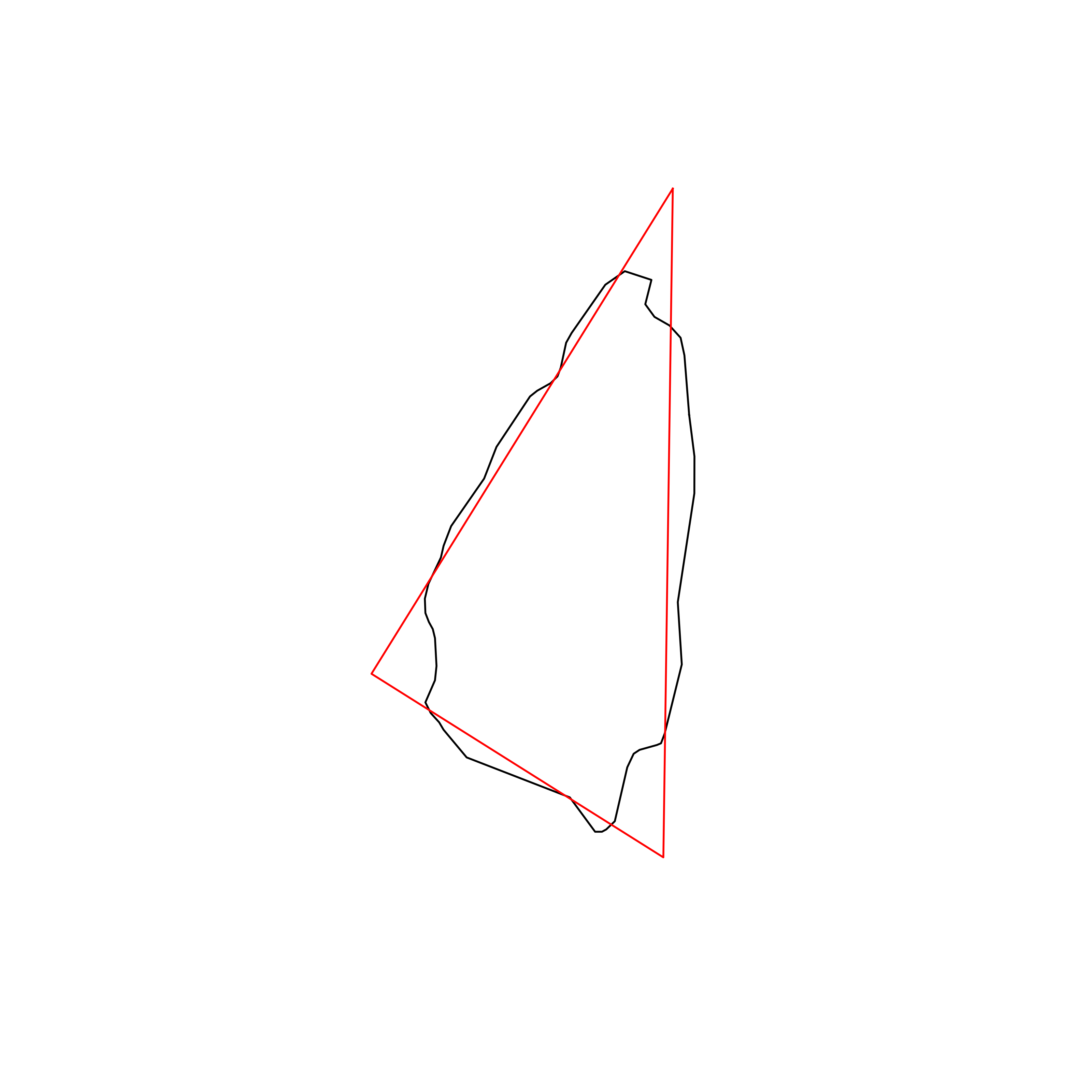 |
| 16 | Mongolia | 0.883835 | 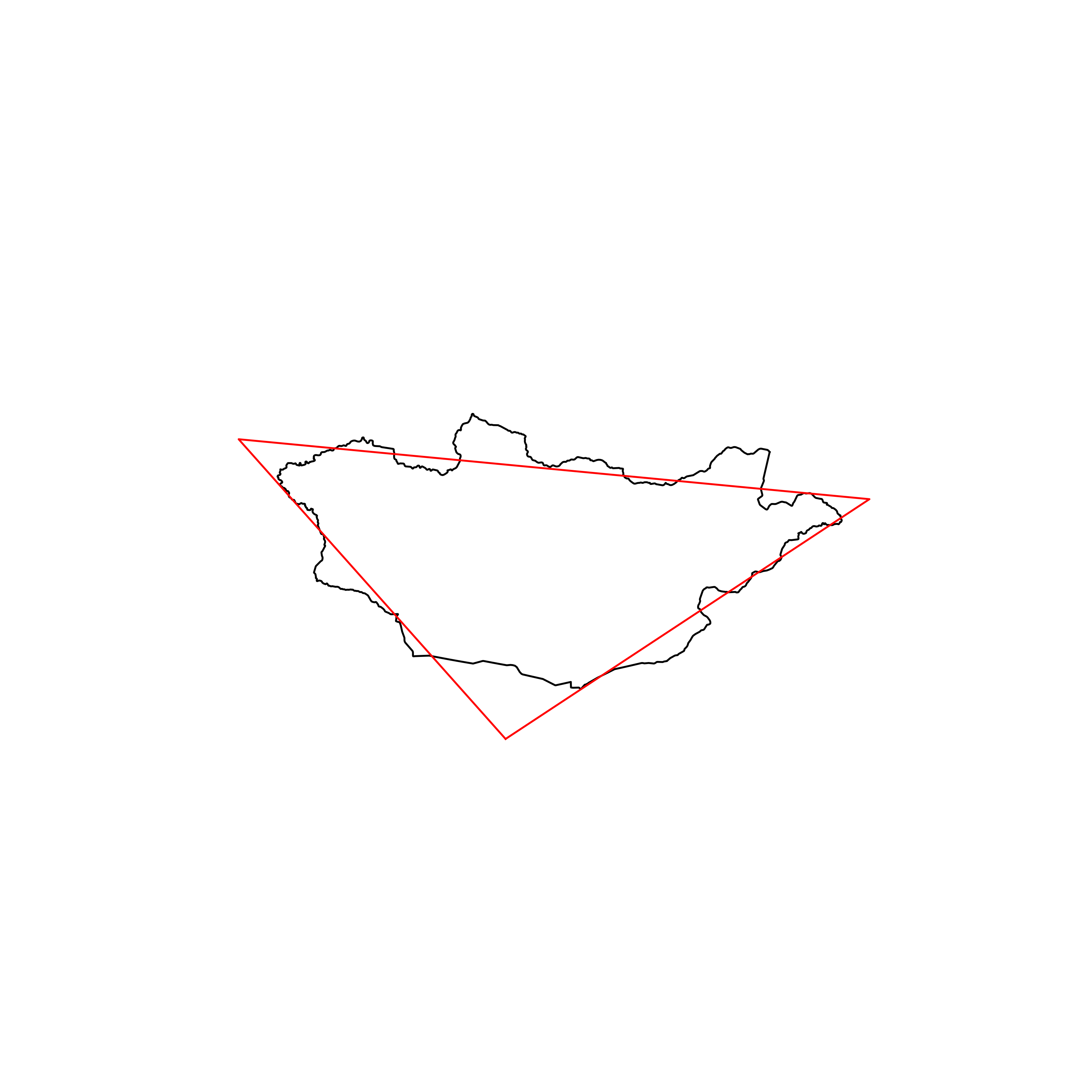 |
| 17 | Finland | 0.883464 | 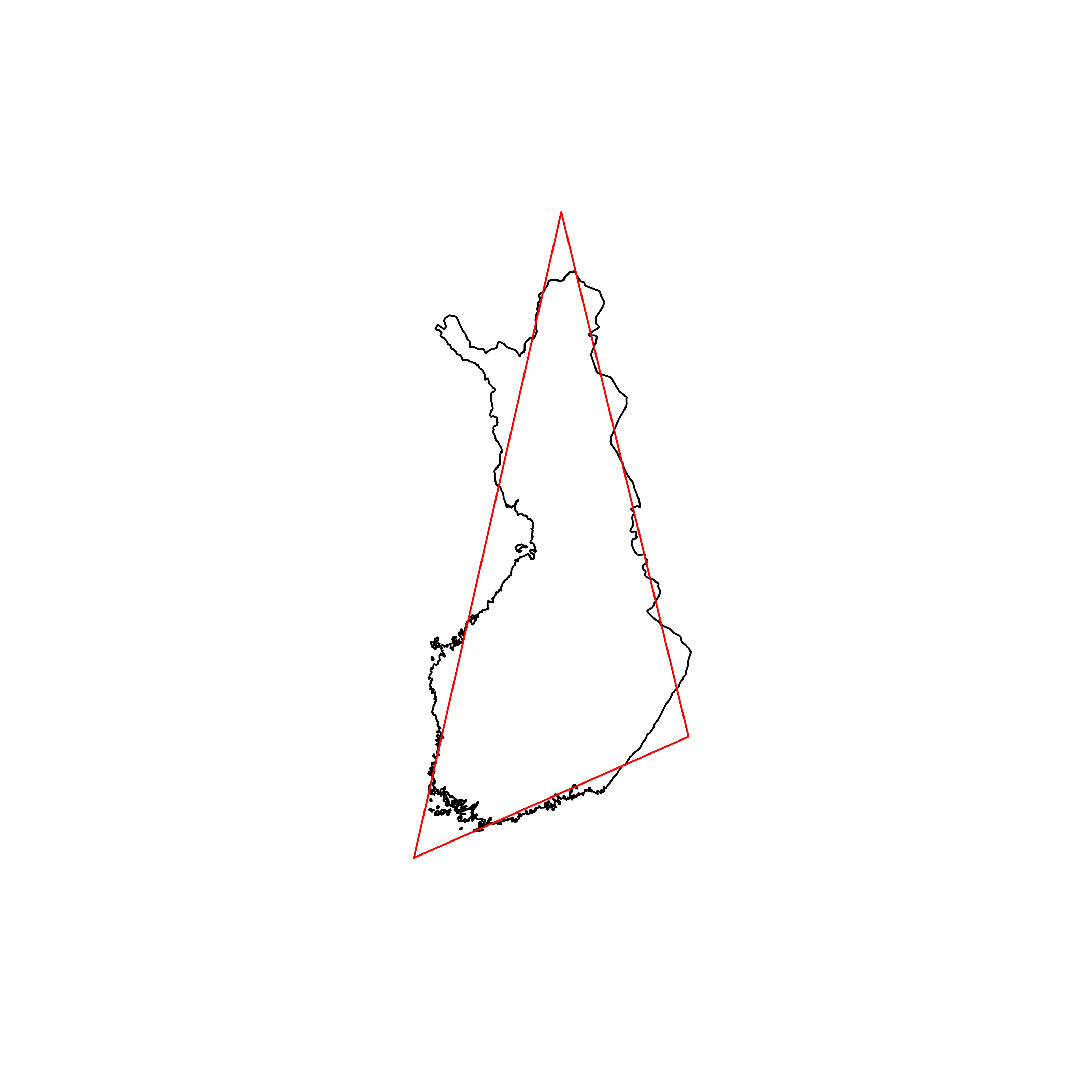 |
| 18 | East Timor | 0.883226 | 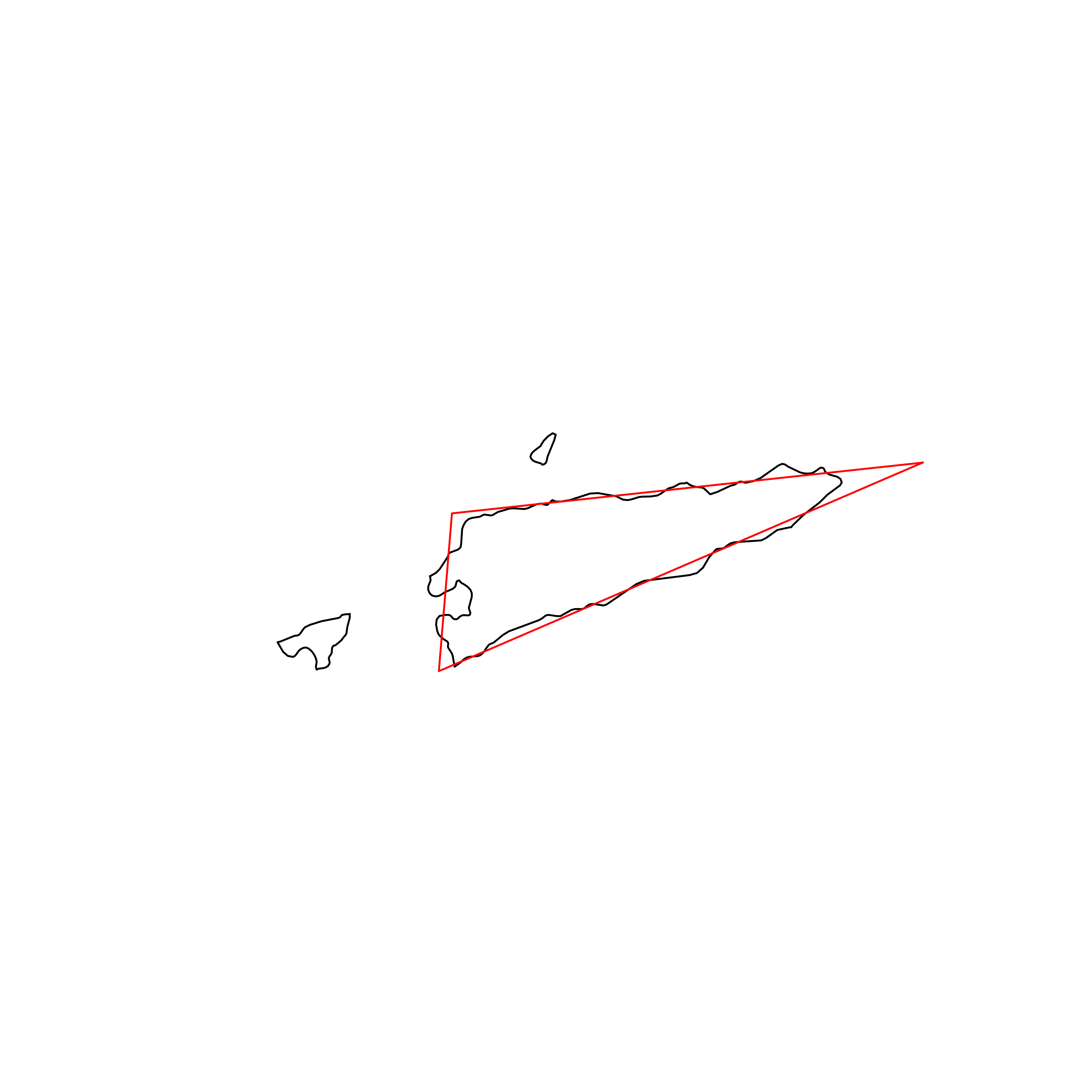 |
| 19 | Lithuania | 0.882420 | 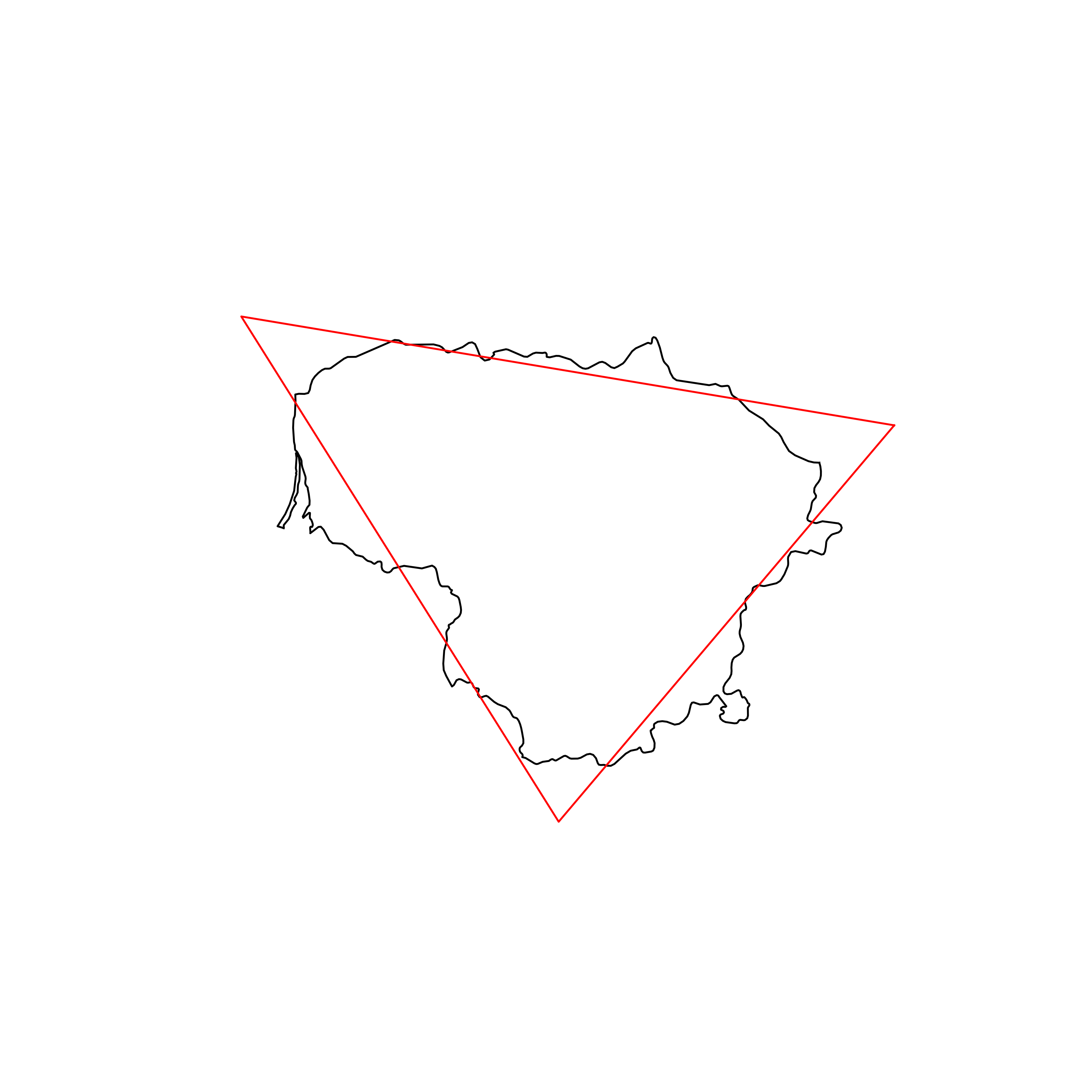 |
| 20 | Spain | 0.880991 | 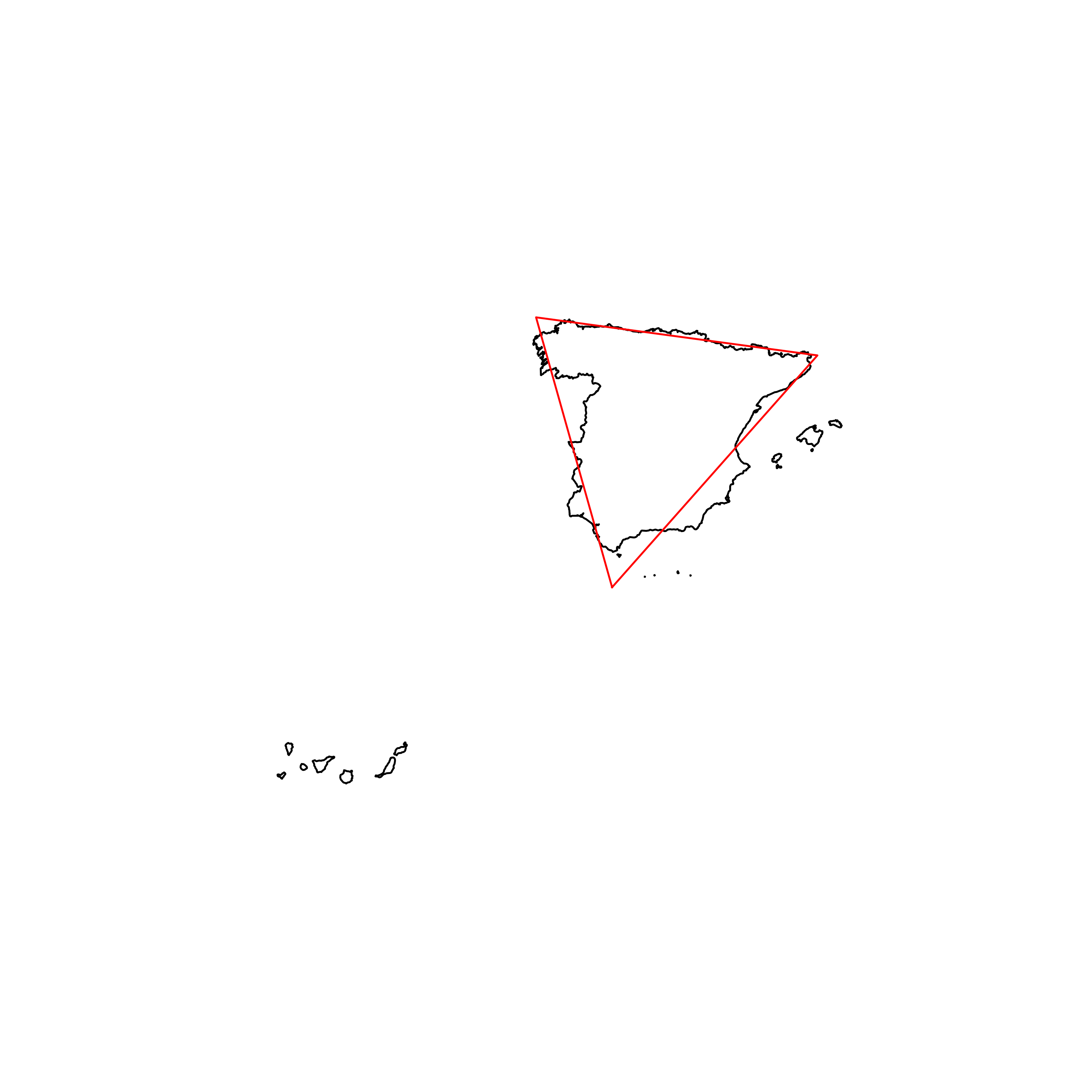 |
| 21 | Iraq | 0.880544 | 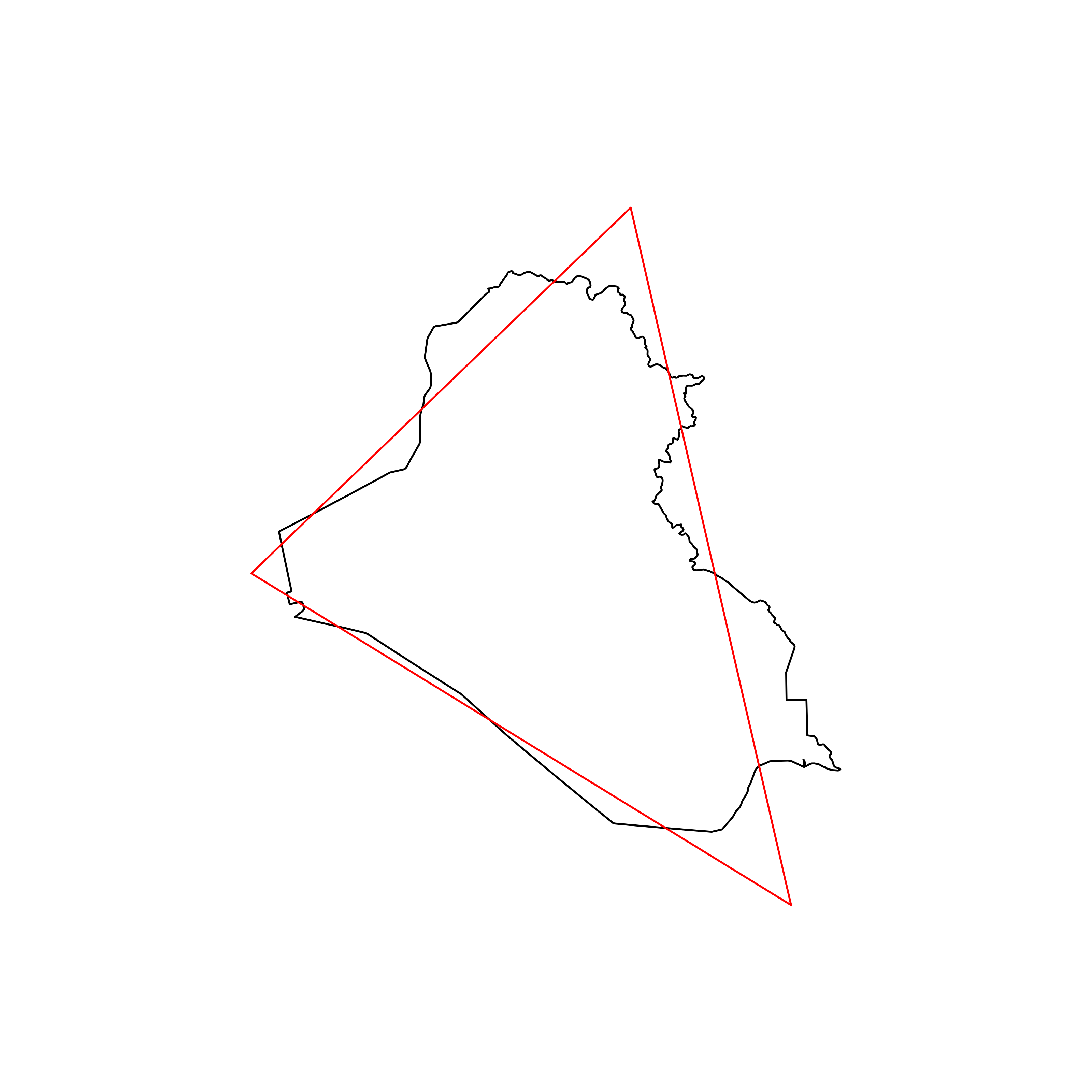 |
| 22 | Nigeria | 0.879989 | 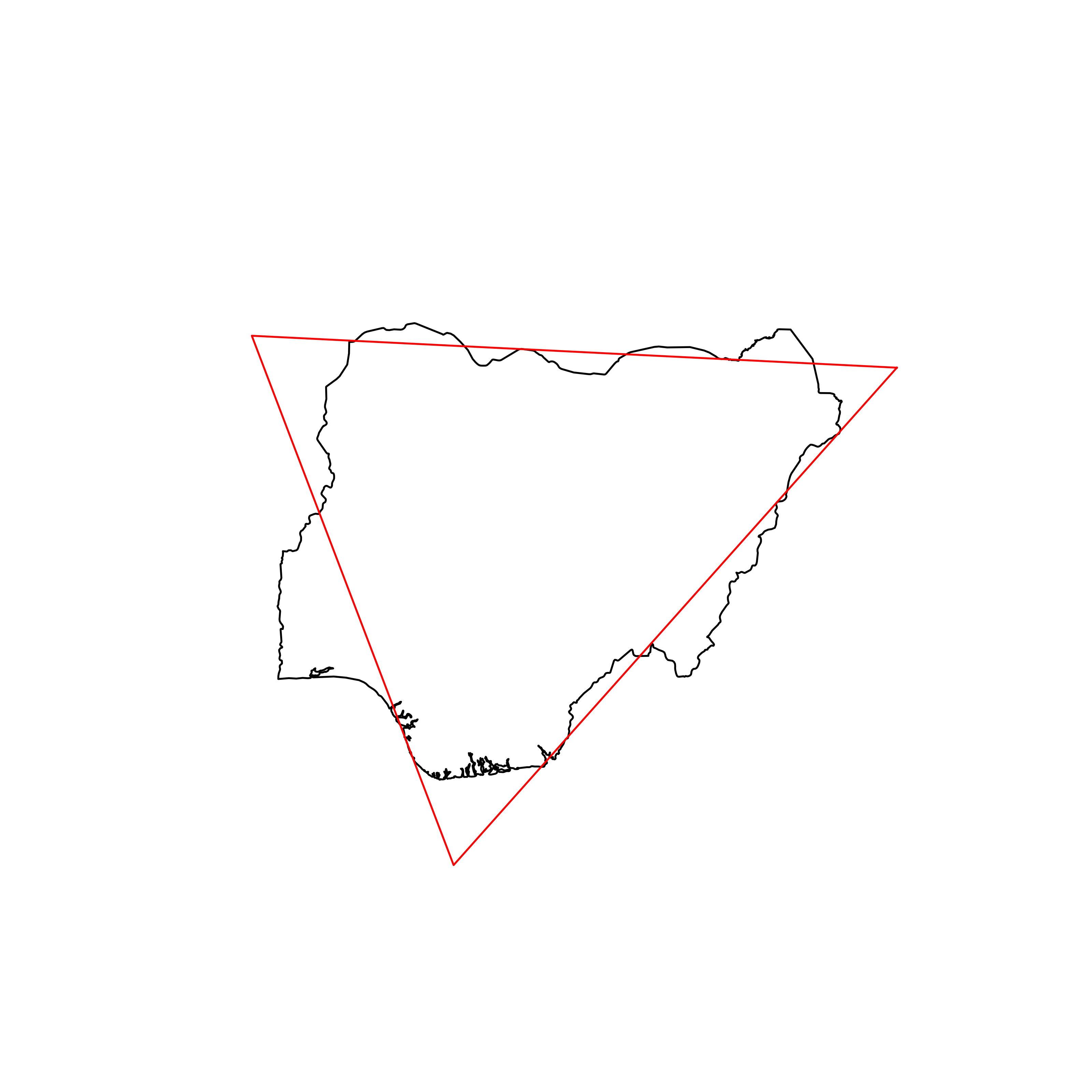 |
| 23 | Bahrain | 0.879084 | 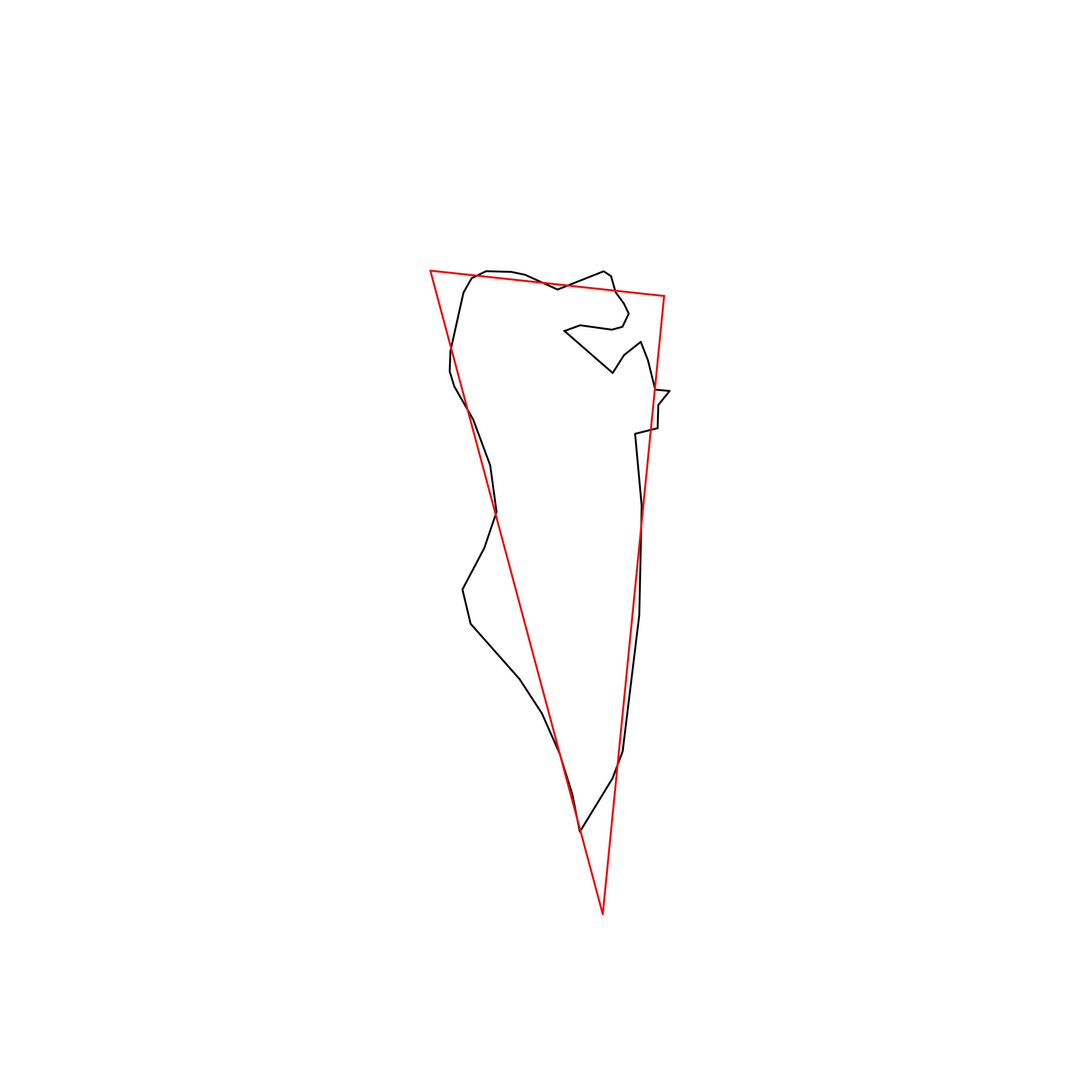 |
| 24 | Central African Republic | 0.878863 | 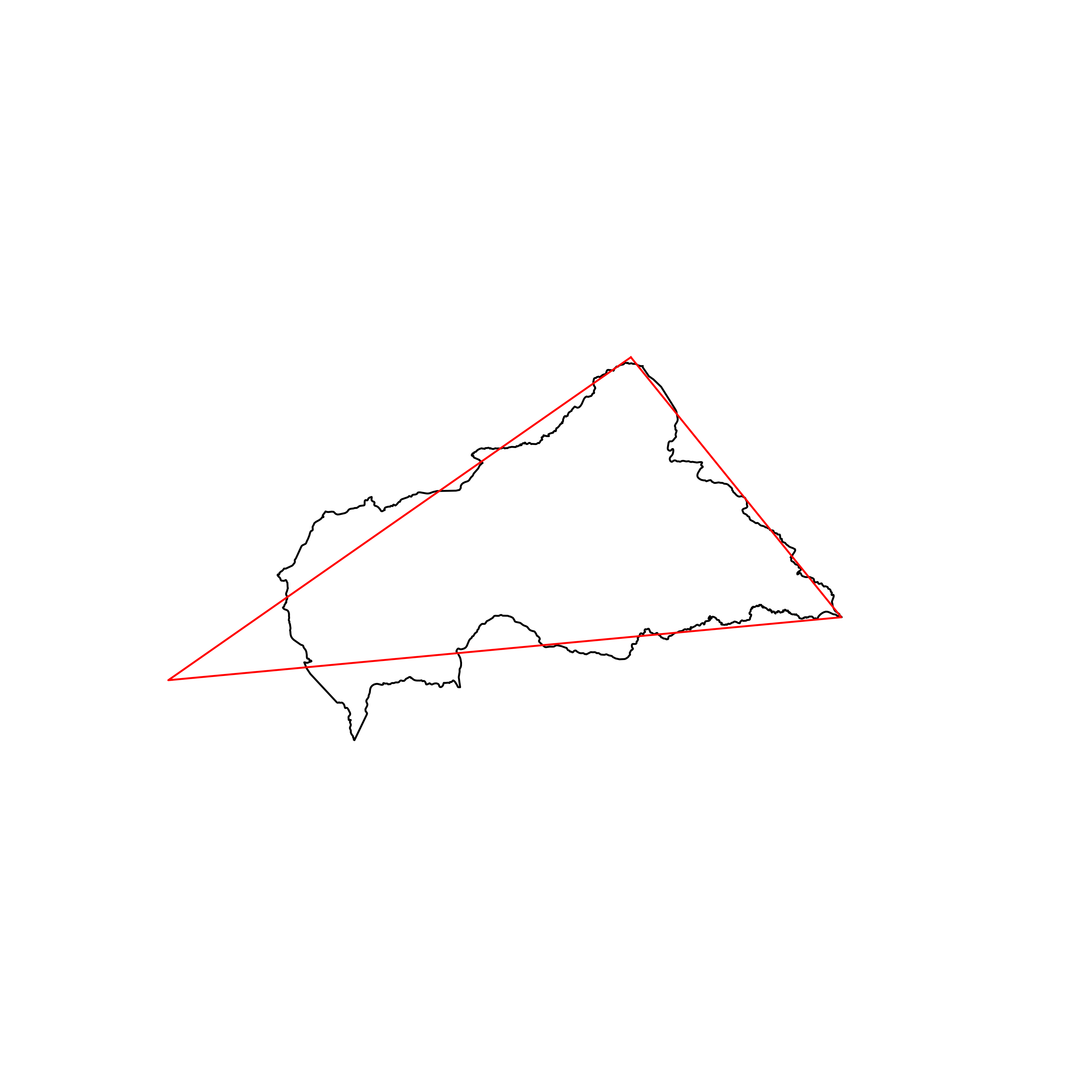 |
| 25 | Niger | 0.878834 | 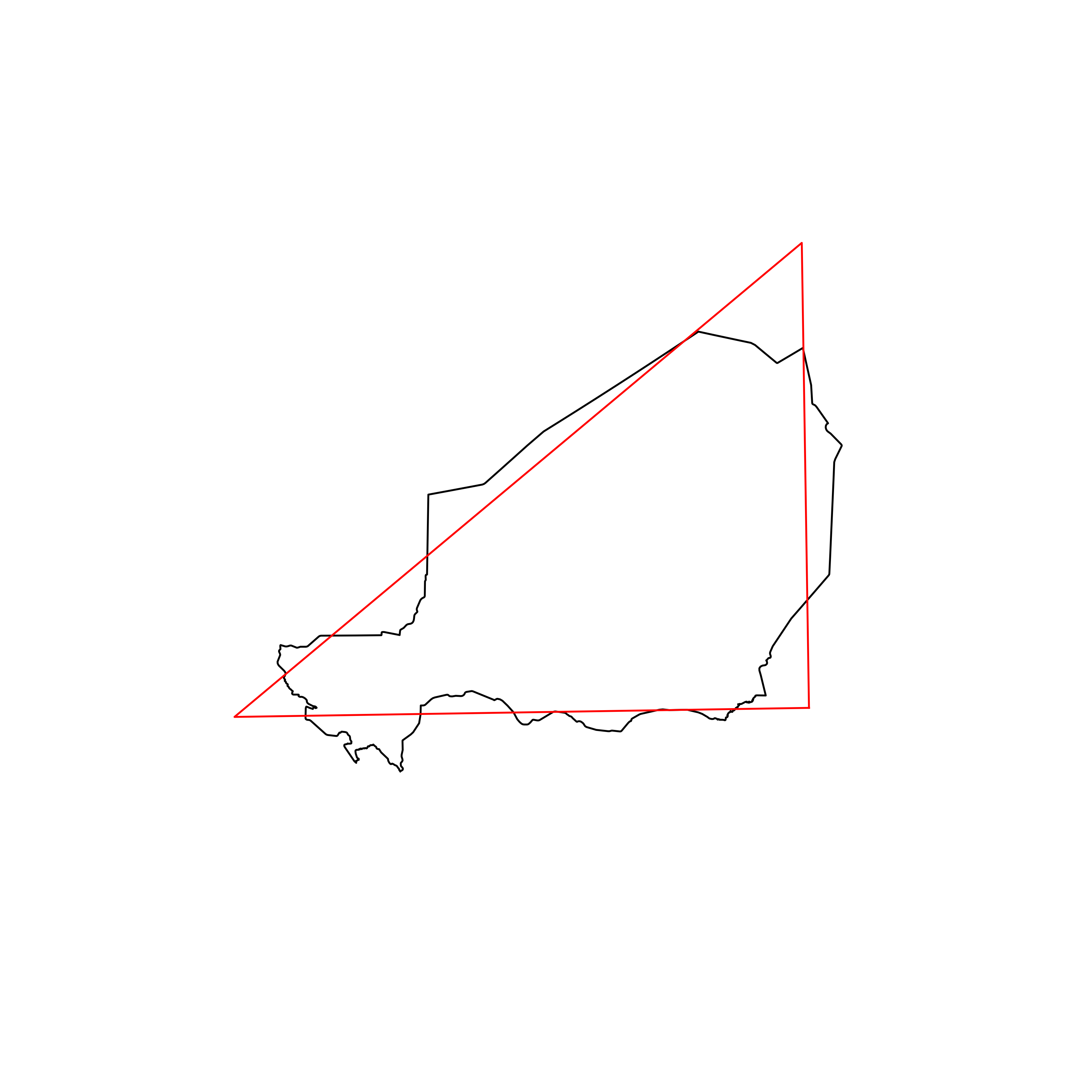 |
| 26 | Cambodia | 0.878727 | 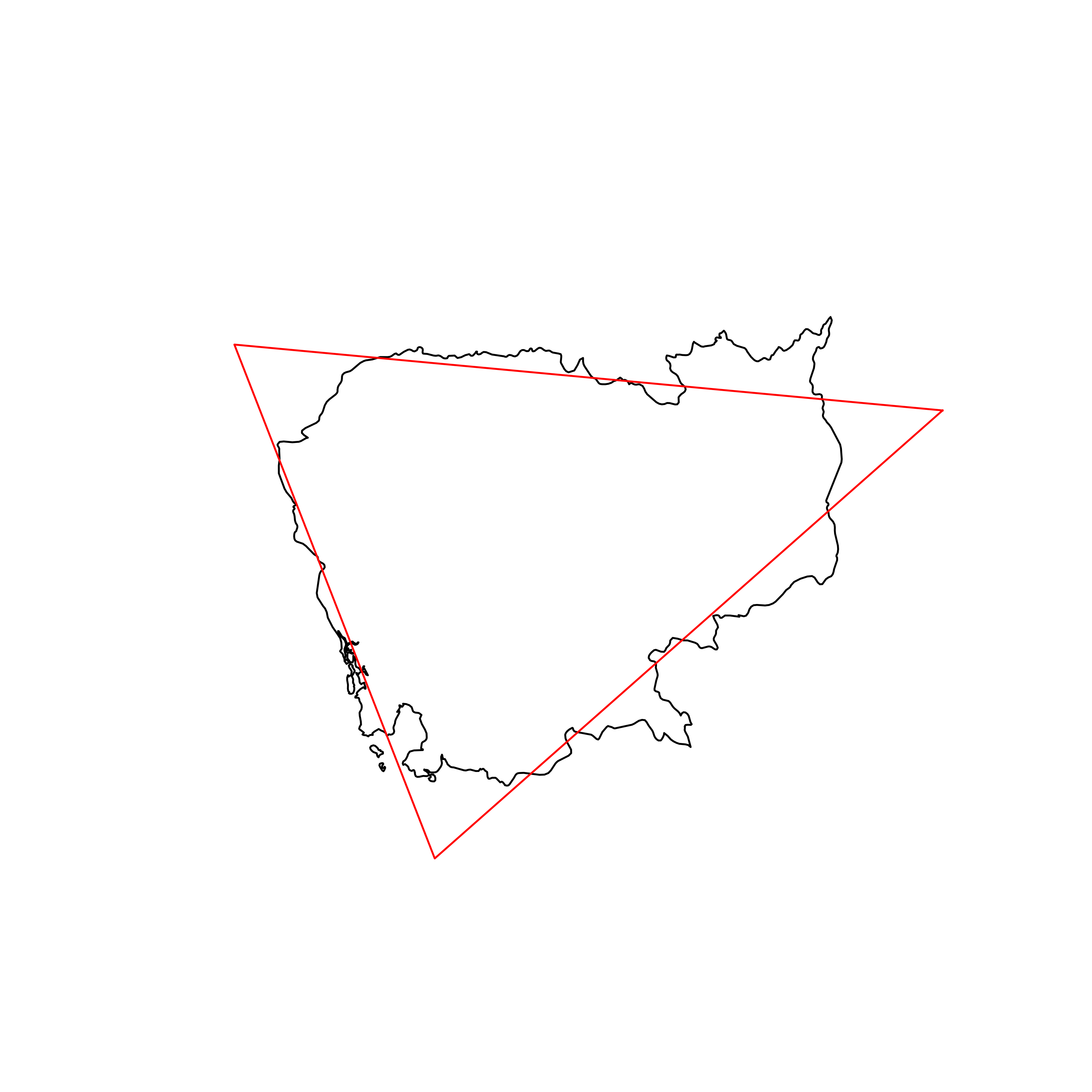 |
| 27 | Libya | 0.878326 | 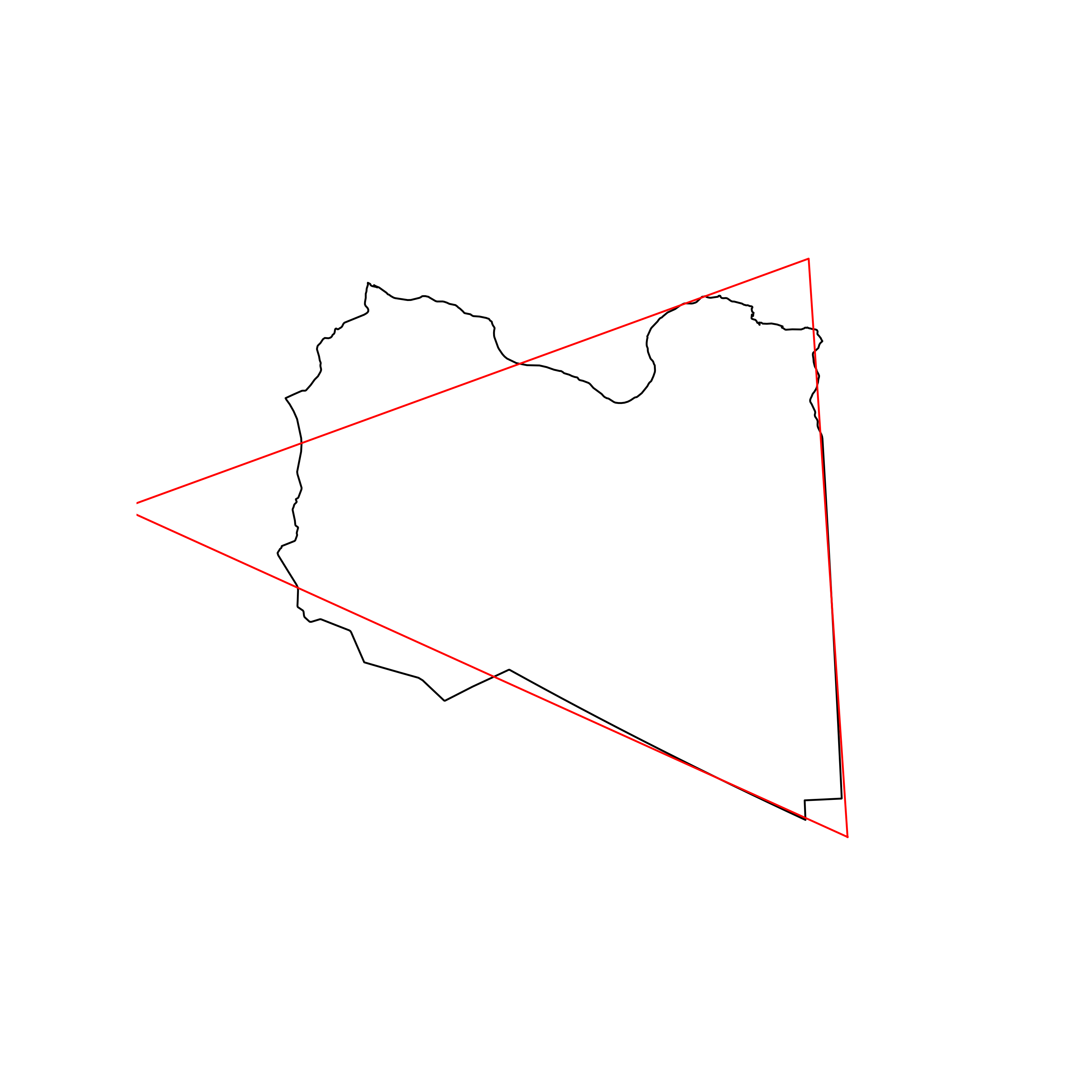 |
| 28 | Lebanon | 0.877776 | 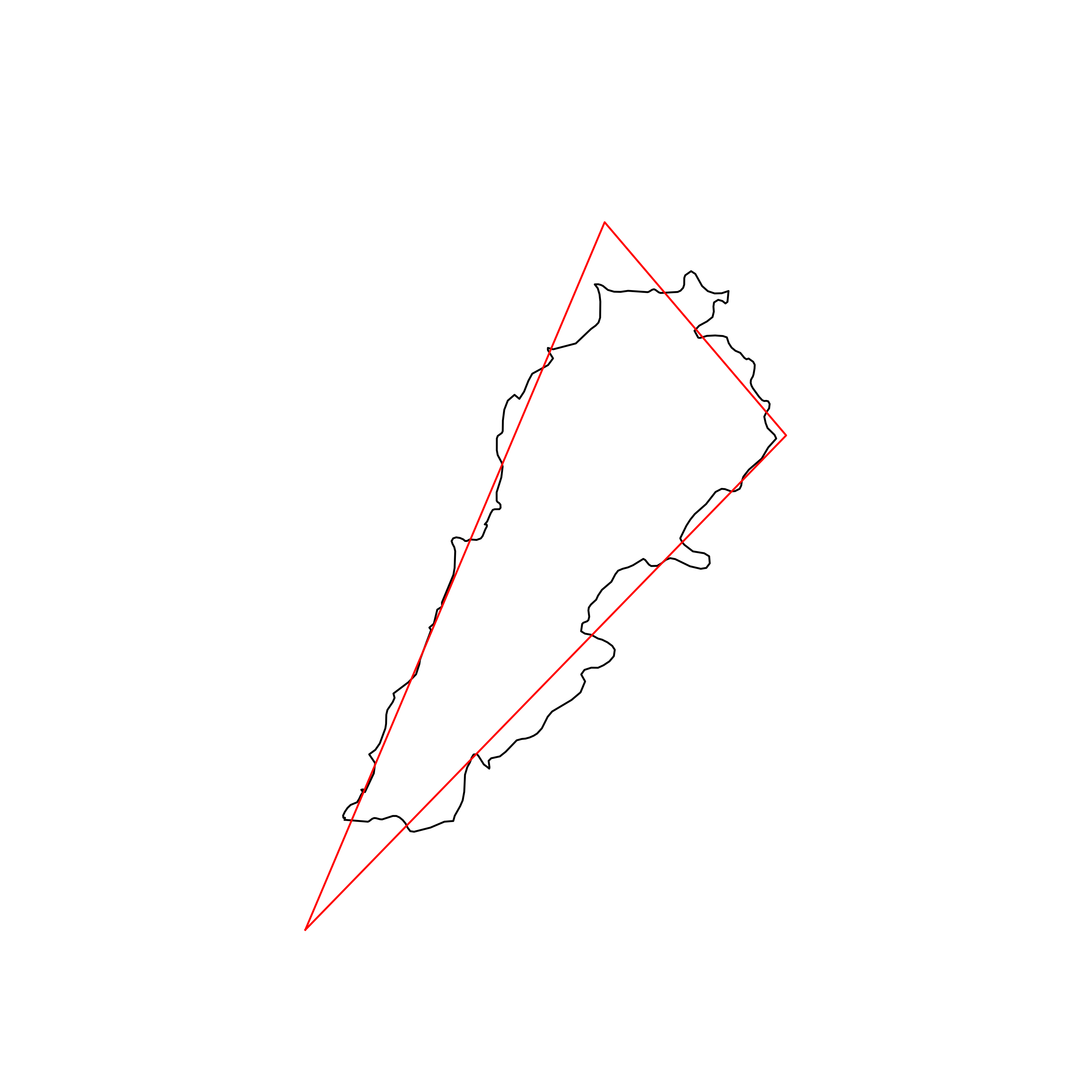 |
| 29 | Chad | 0.876590 | 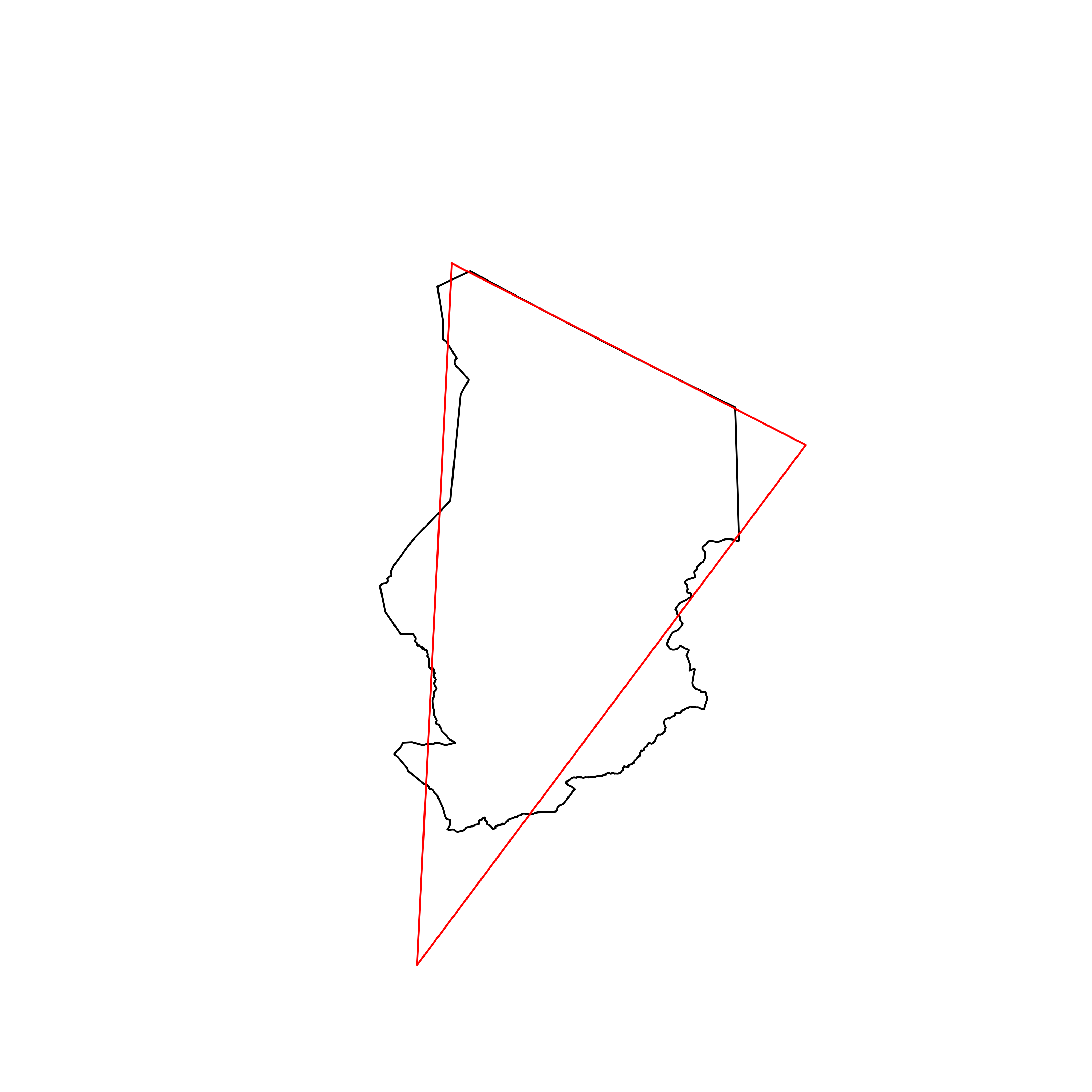 |
| 30 | Dominica | 0.875869 | 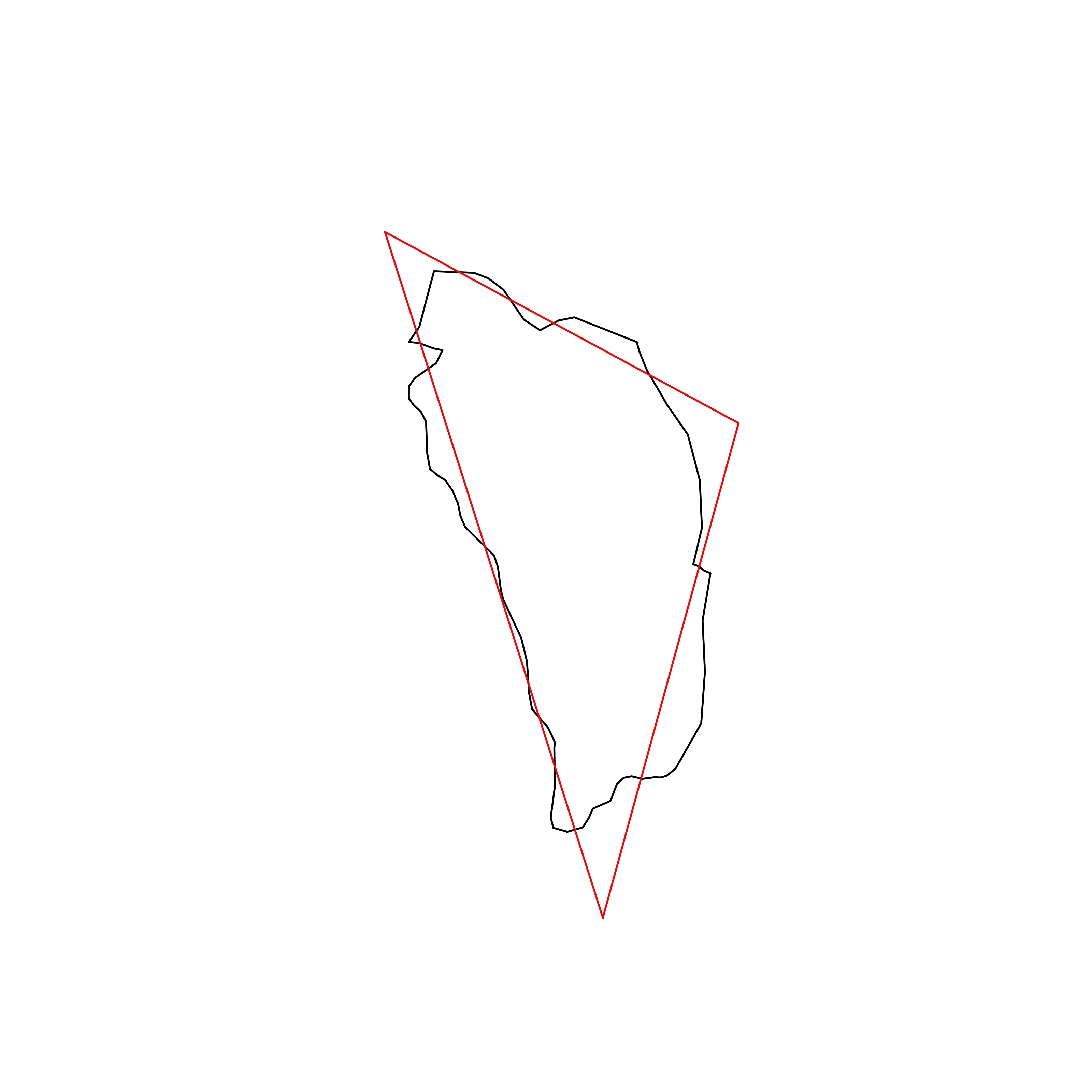 |
| 31 | Taiwan | 0.875187 | 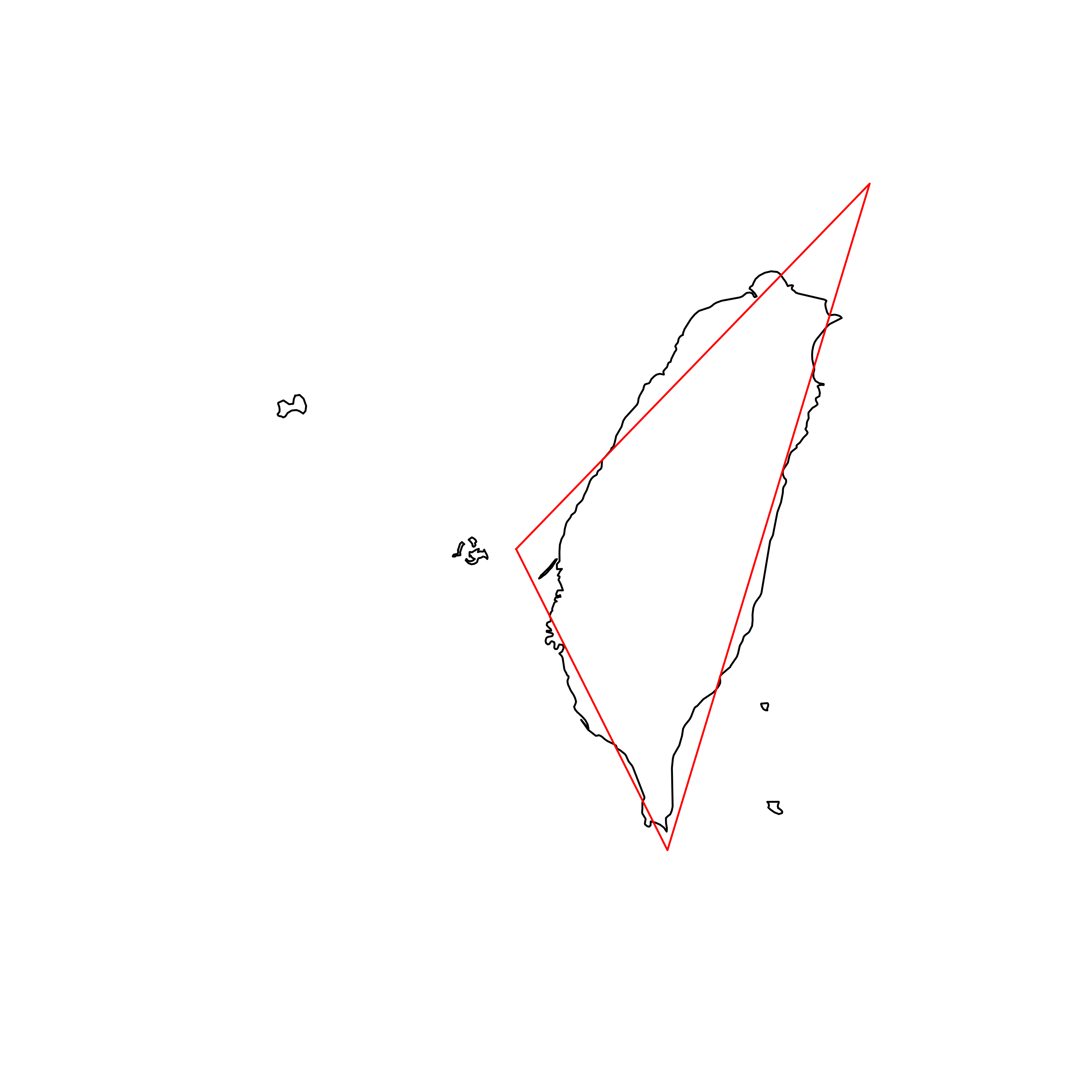 |
| 32 | Brazil | 0.874508 | 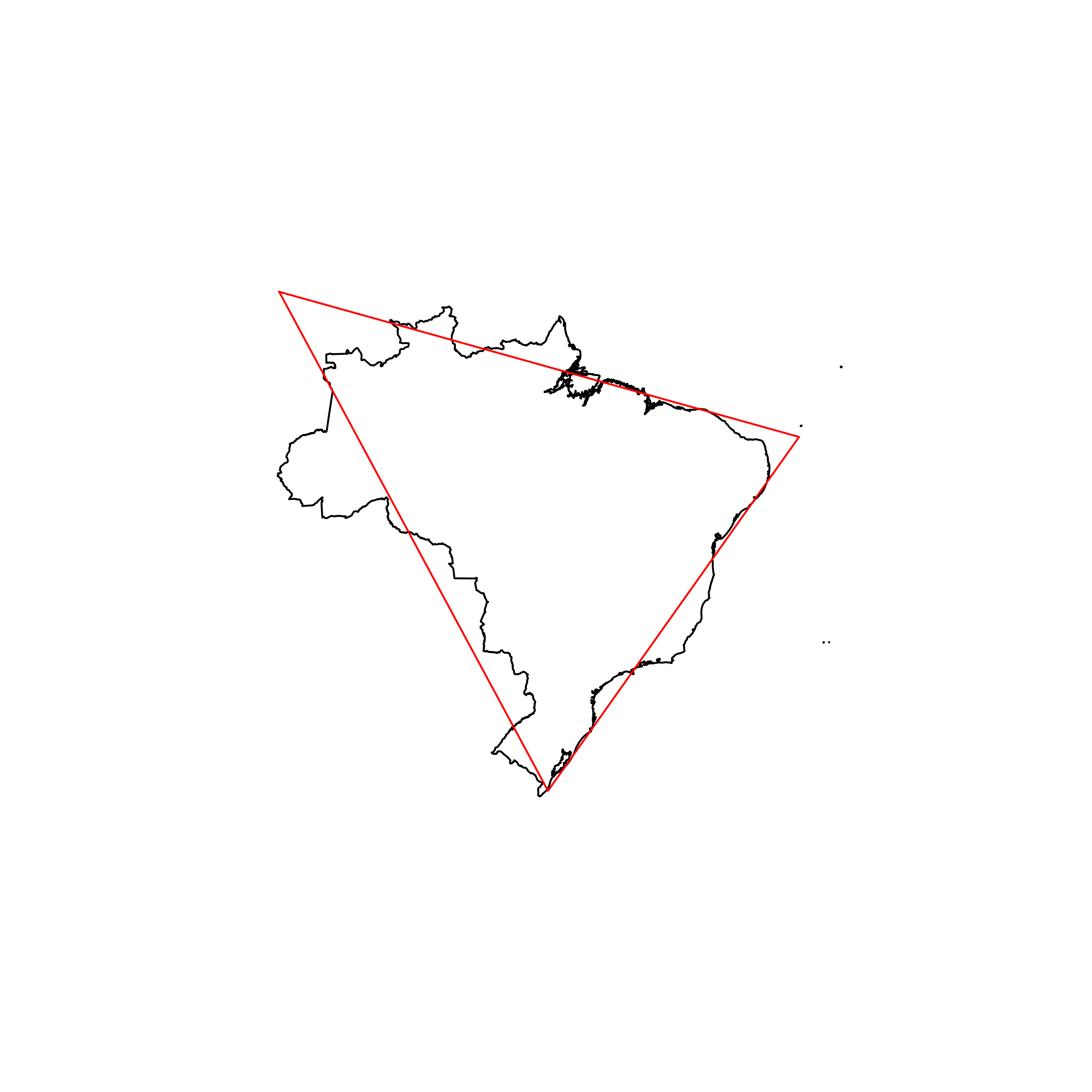 |
| 33 | Saudi Arabia | 0.874421 | 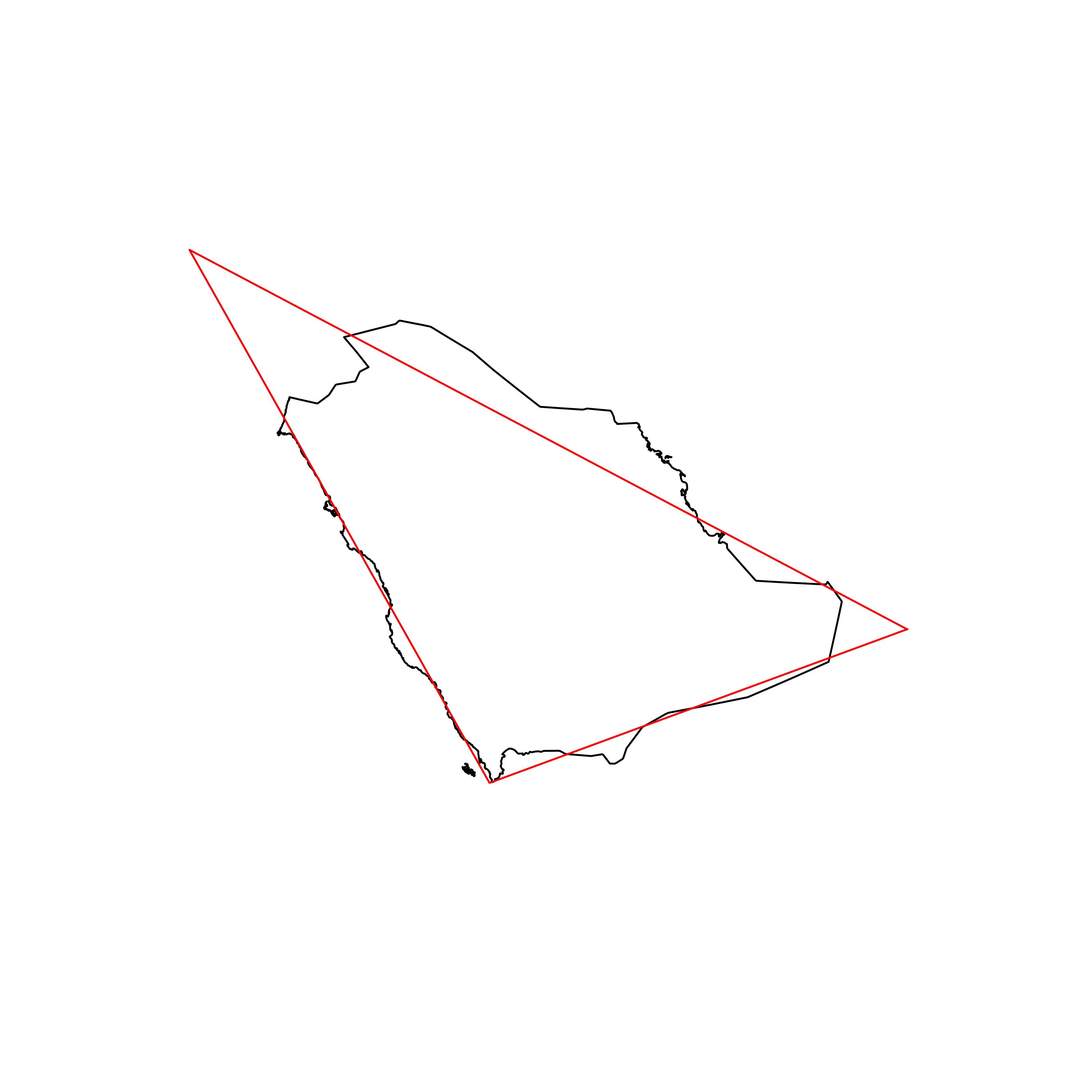 |
| 34 | Zimbabwe | 0.874192 | 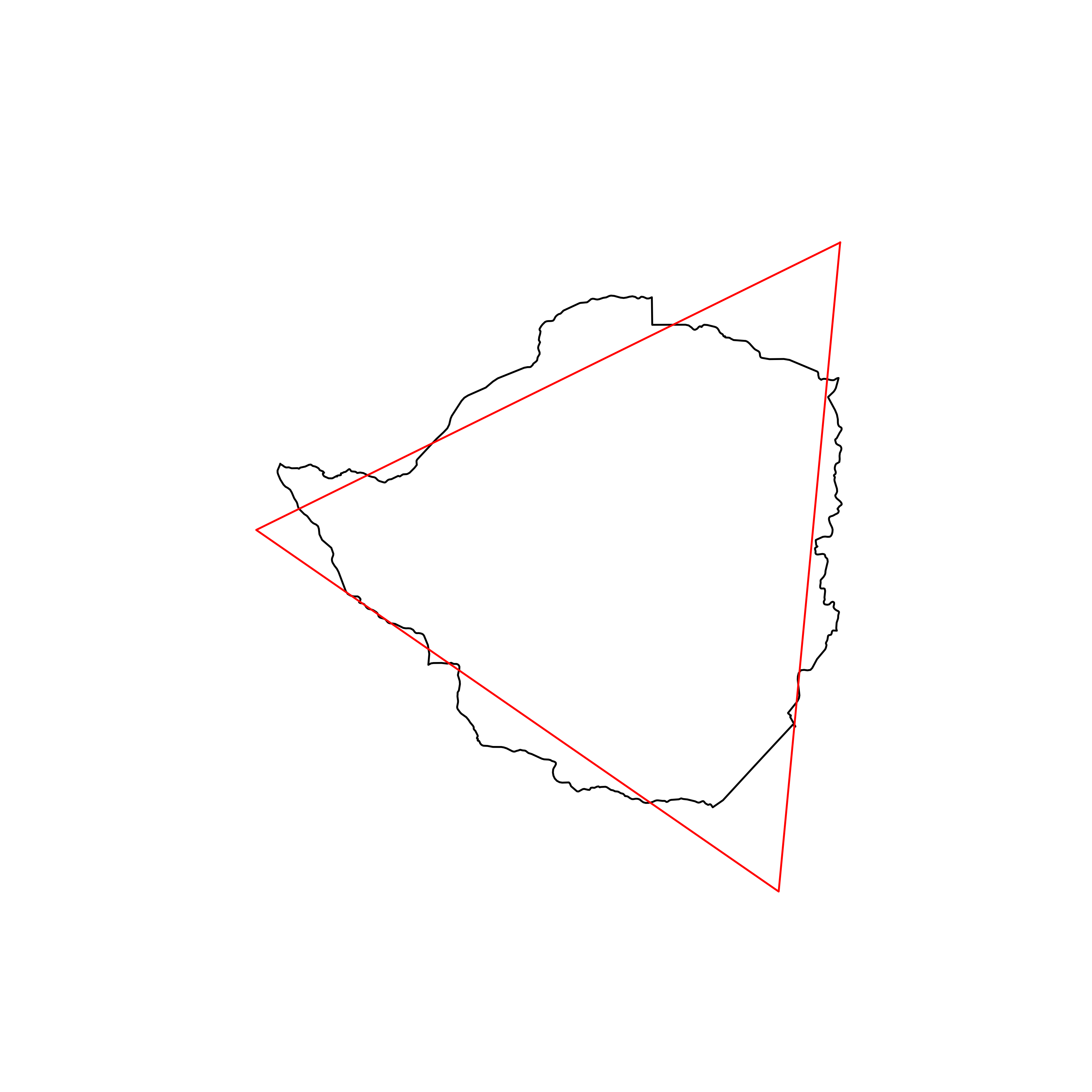 |
| 35 | Ecuador | 0.872448 | 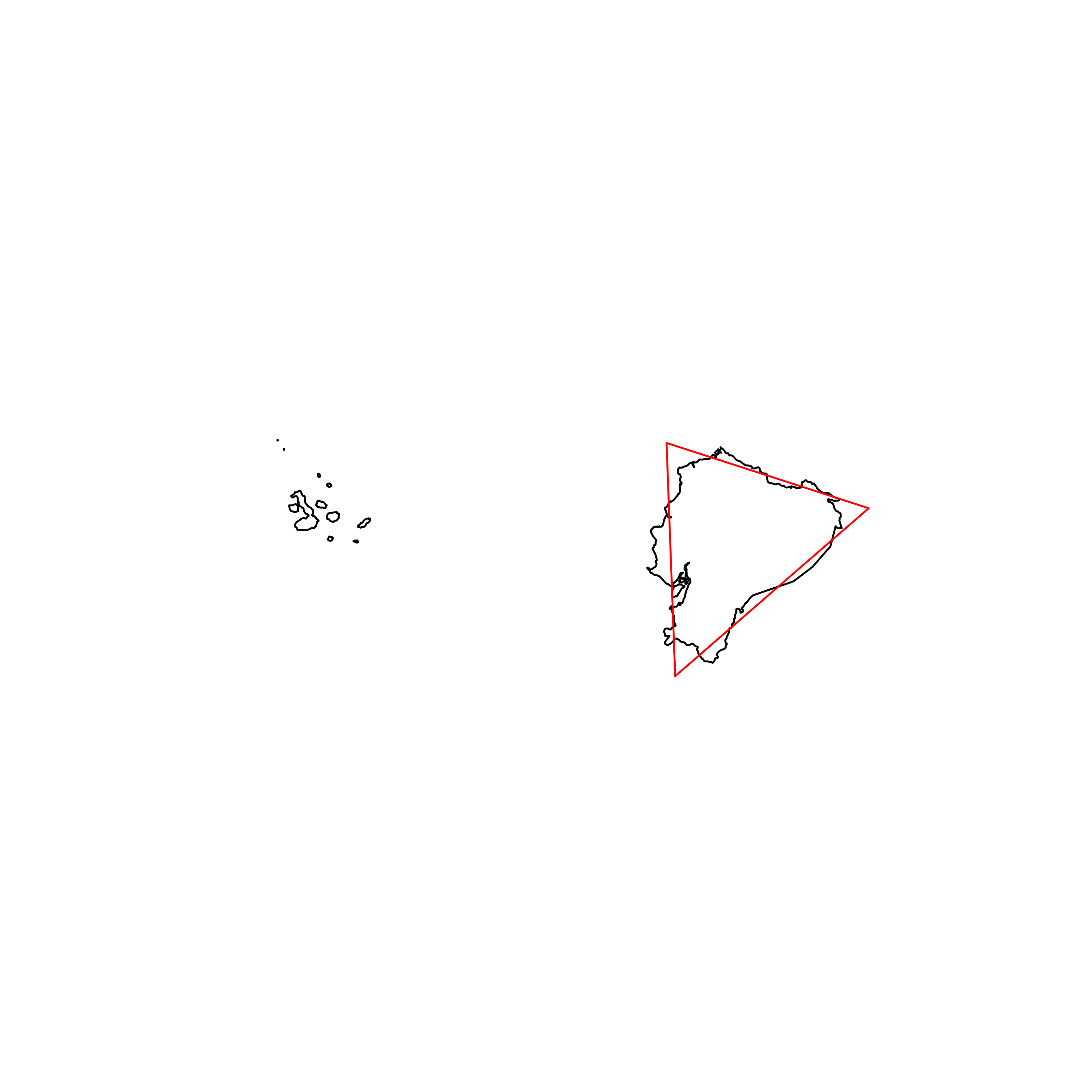 |
| 36 | Venezuela | 0.871525 | 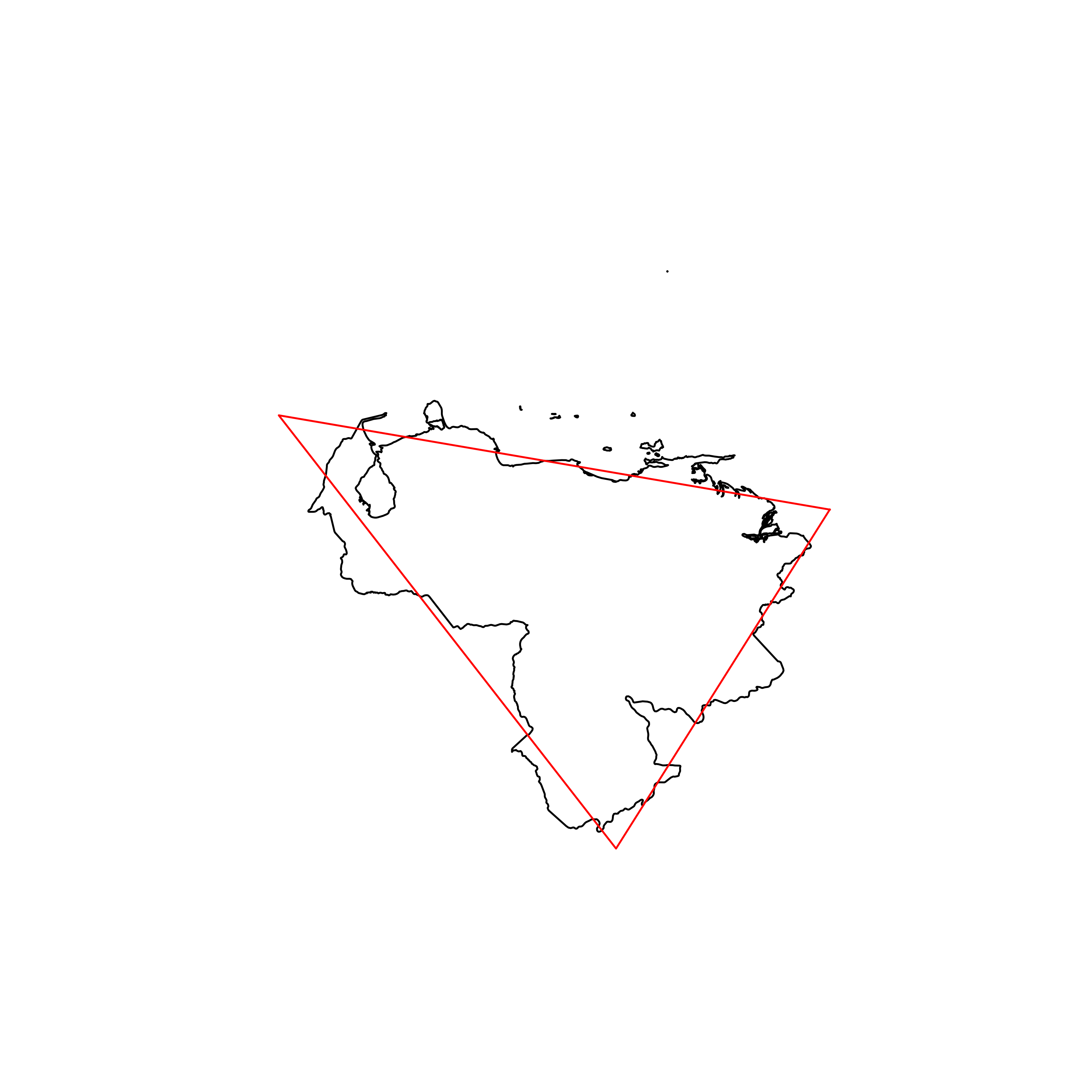 |
| 37 | Uruguay | 0.869709 | 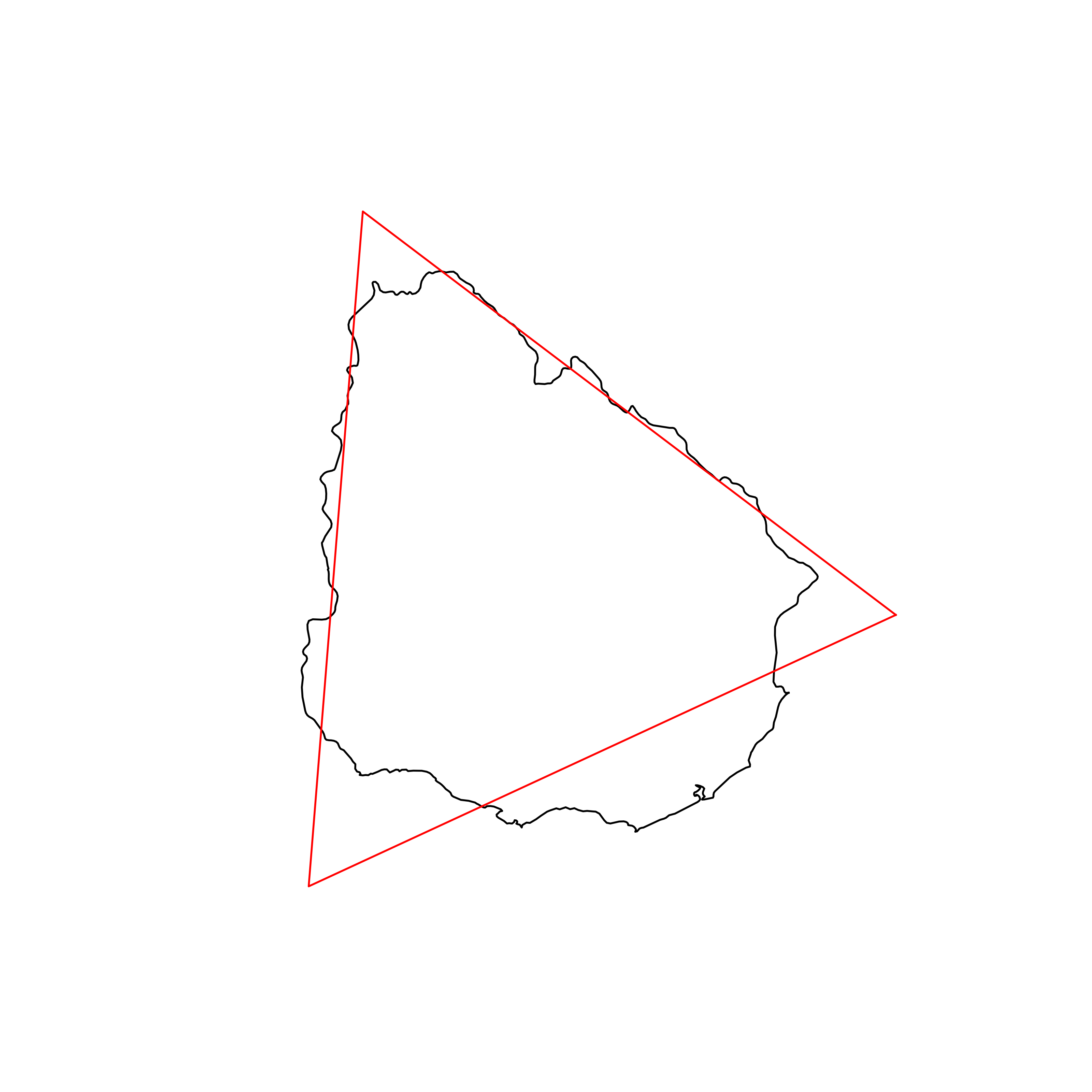 |
| 38 | Benin | 0.868978 | 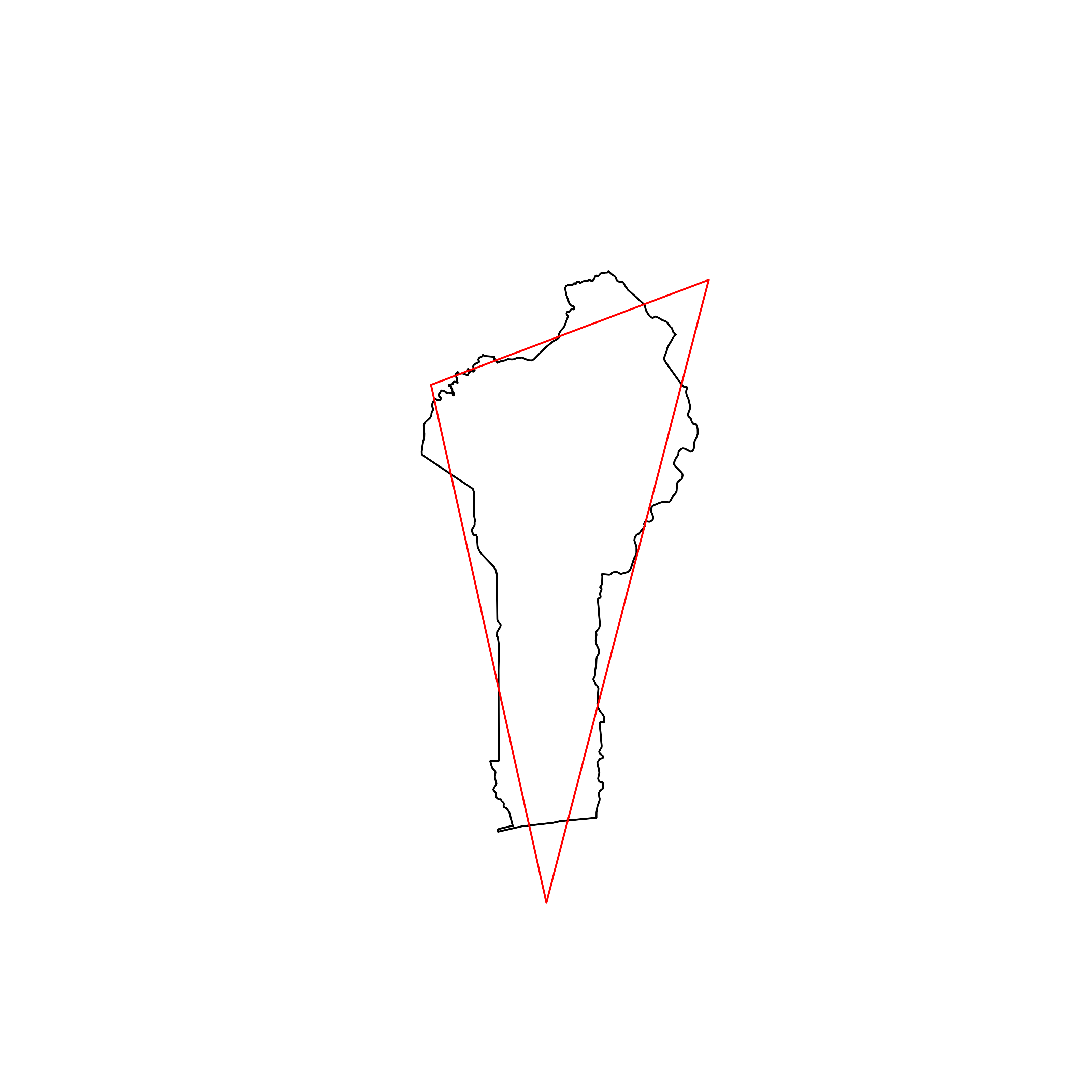 |
| 39 | Liberia | 0.868948 | 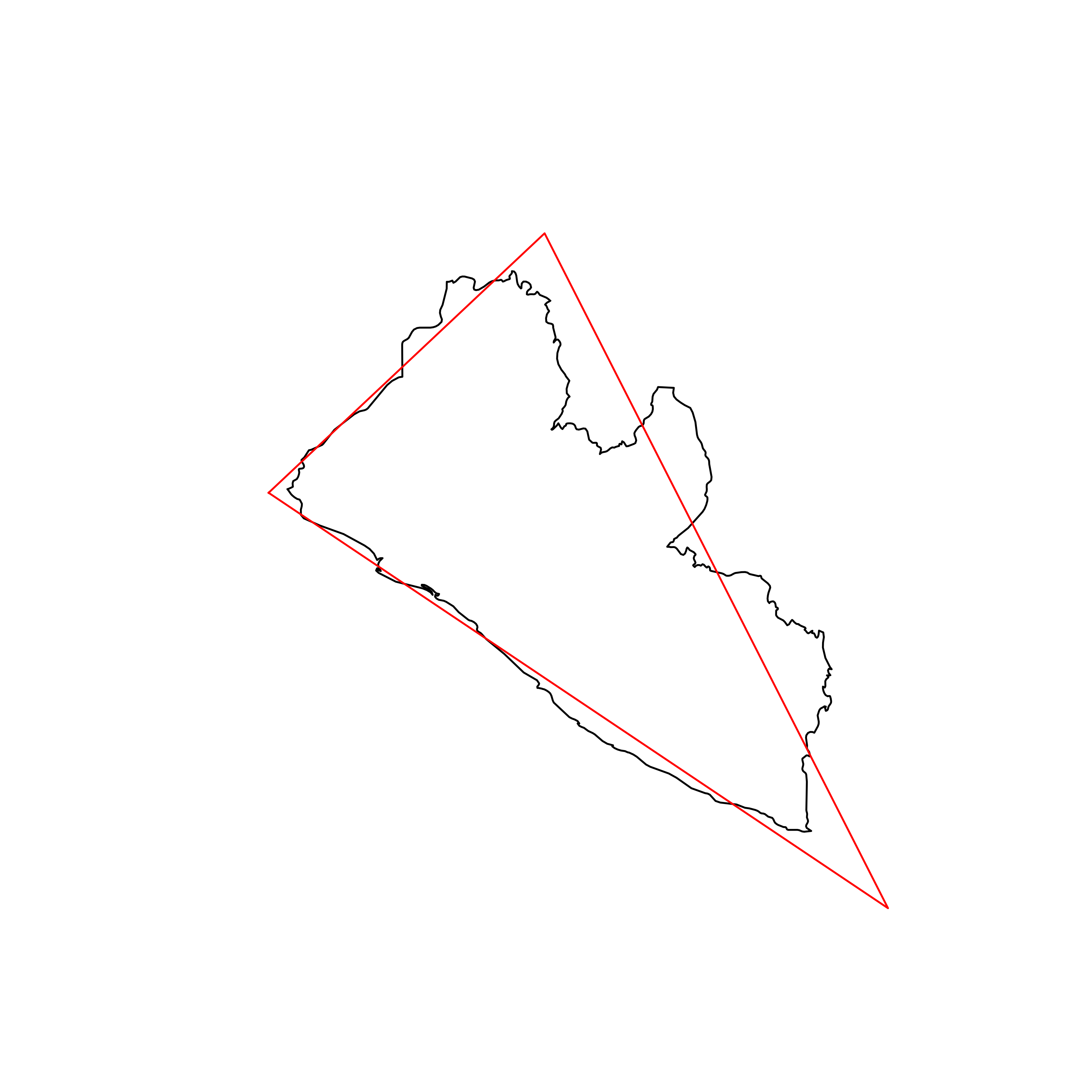 |
| 40 | Madagascar | 0.867805 |  |
| 41 | Democratic Republic of the Congo | 0.866893 | 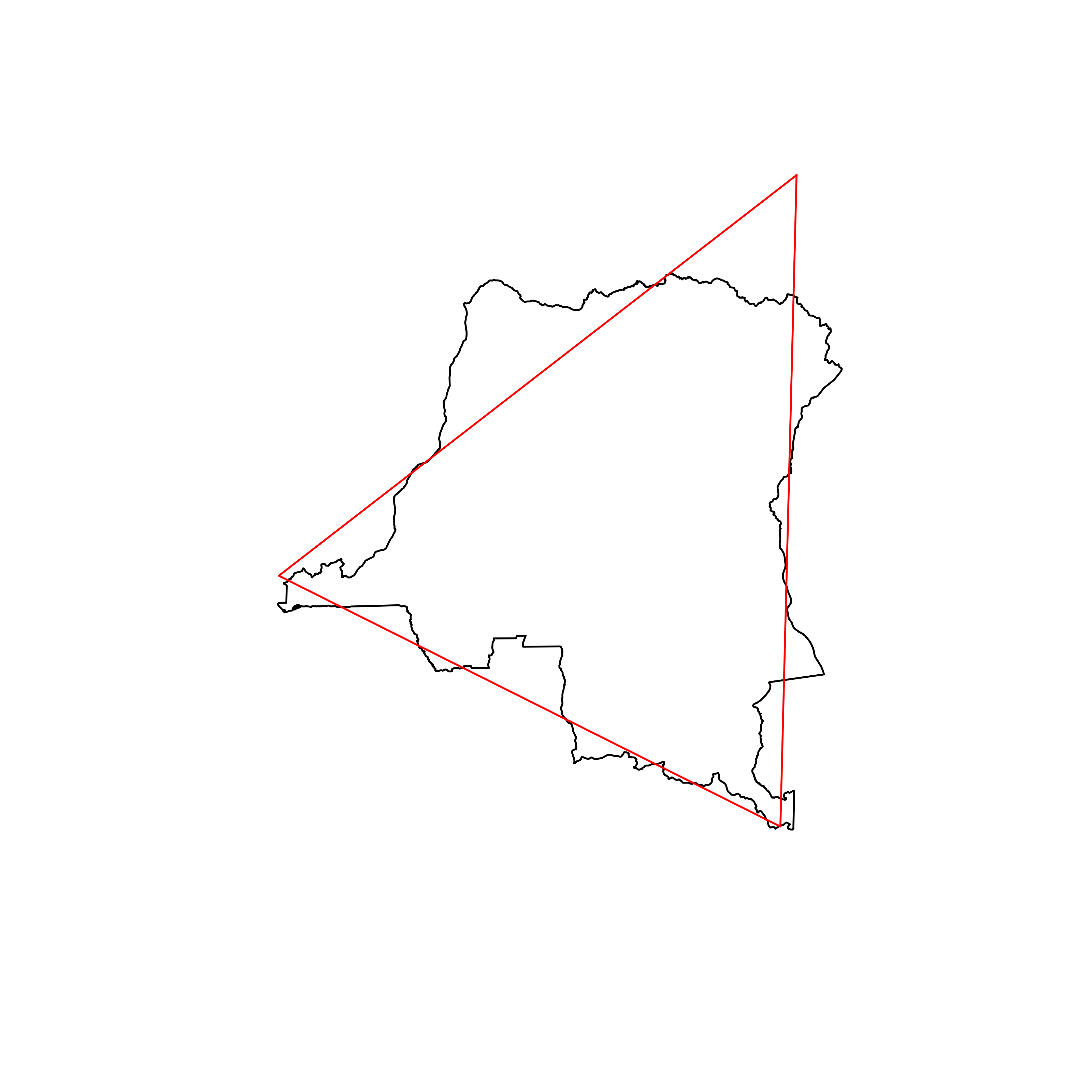 |
| 42 | Ethiopia | 0.866403 | 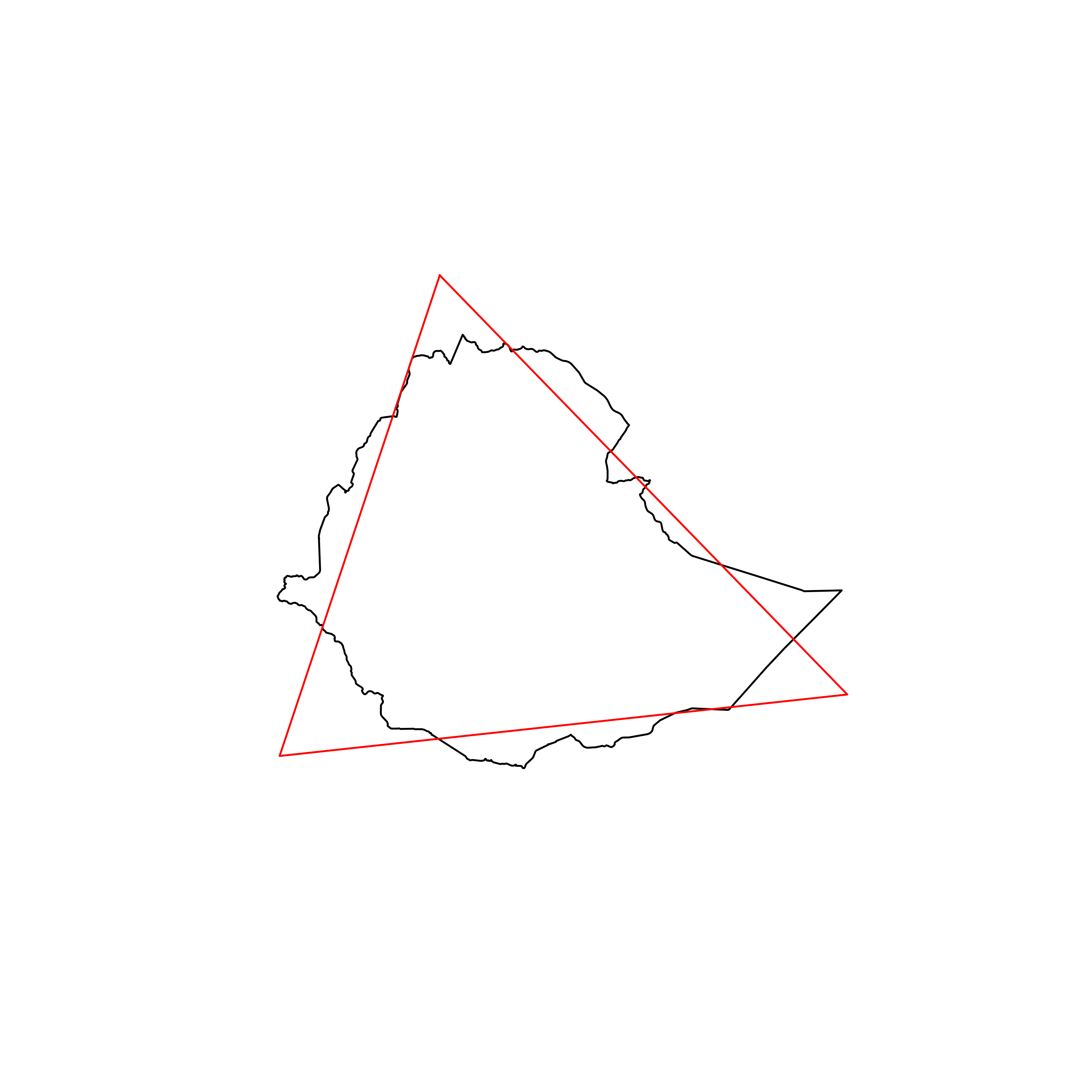 |
| 43 | Syria | 0.865422 | 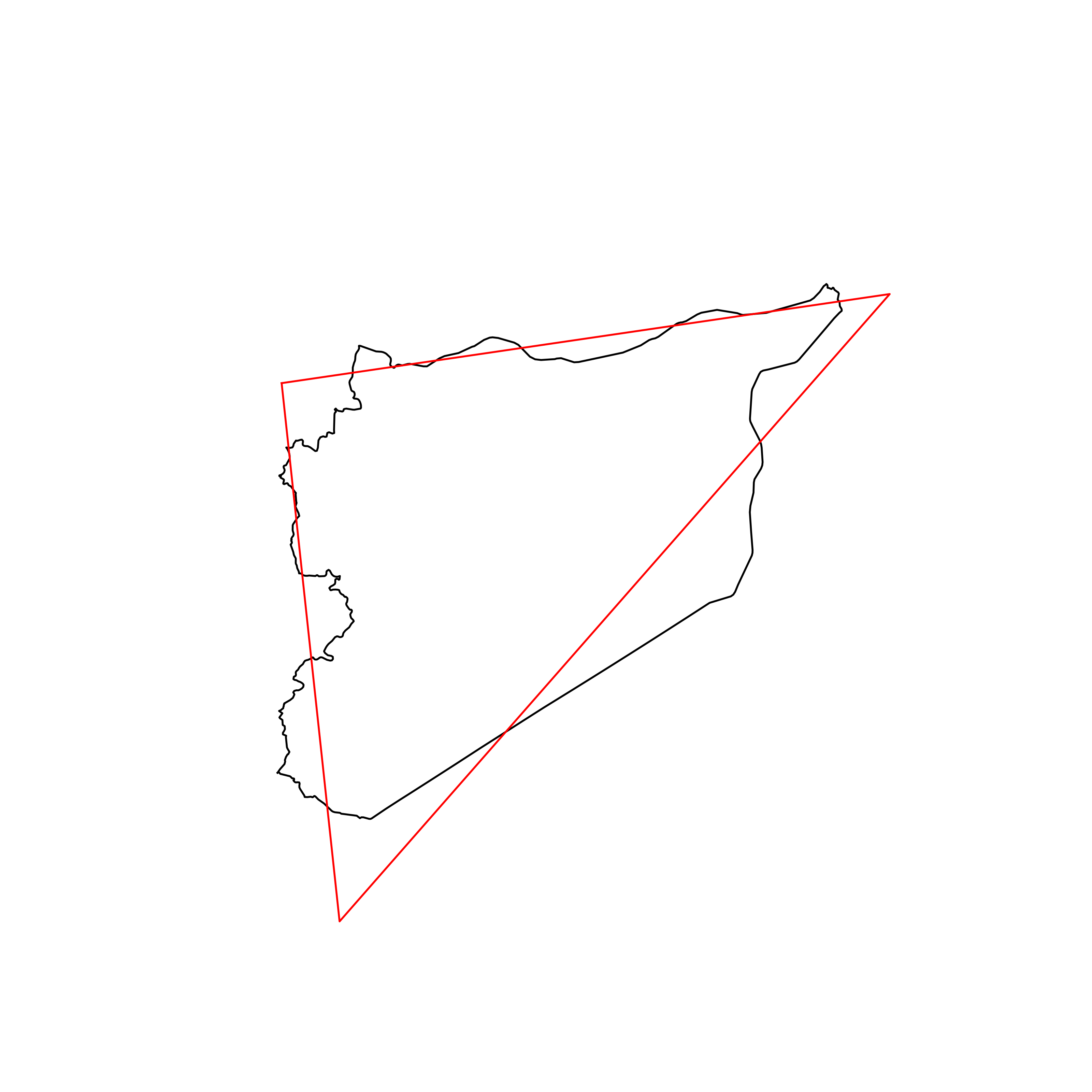 |
| 44 | Slovenia | 0.864037 | 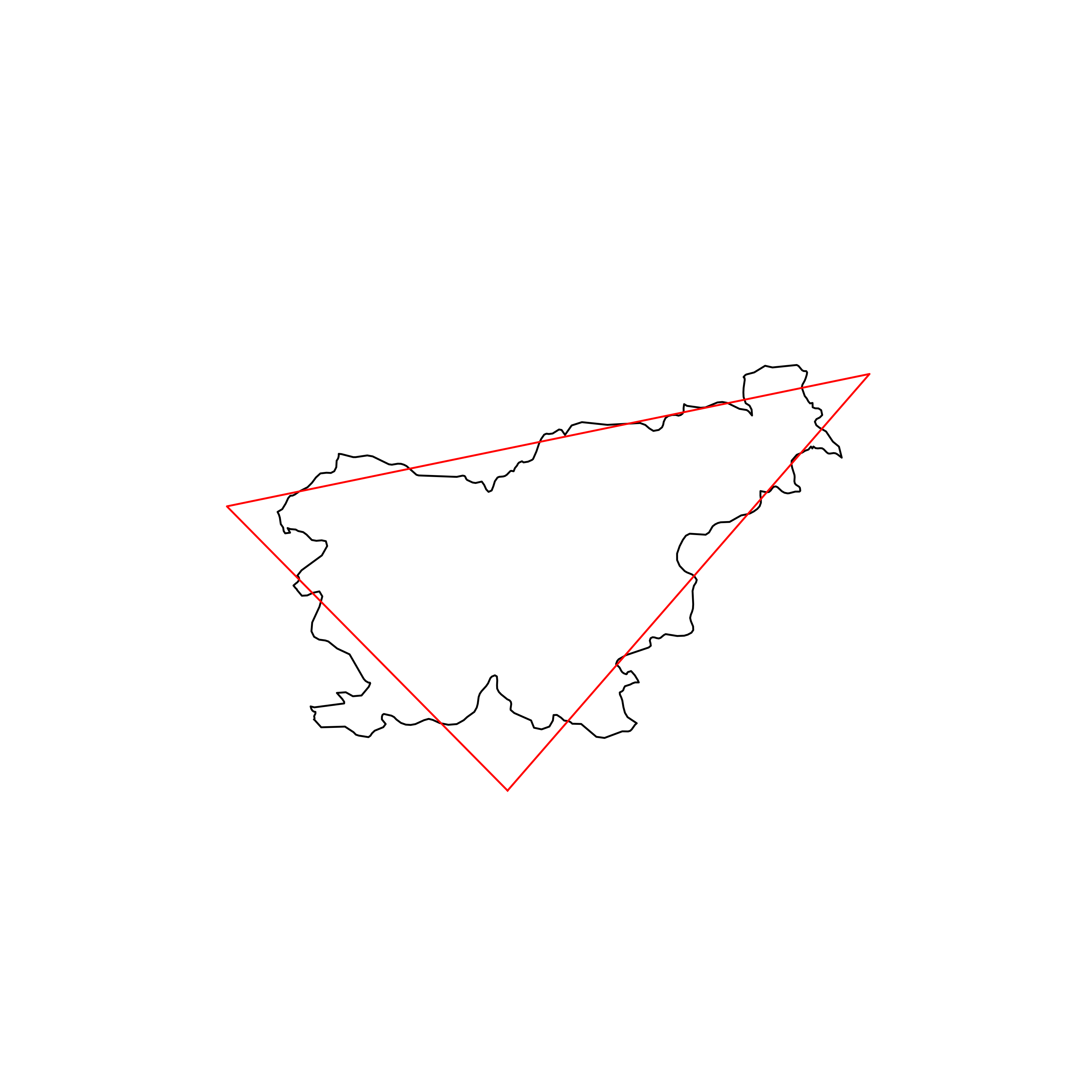 |
| 45 | Liechtenstein | 0.863911 | 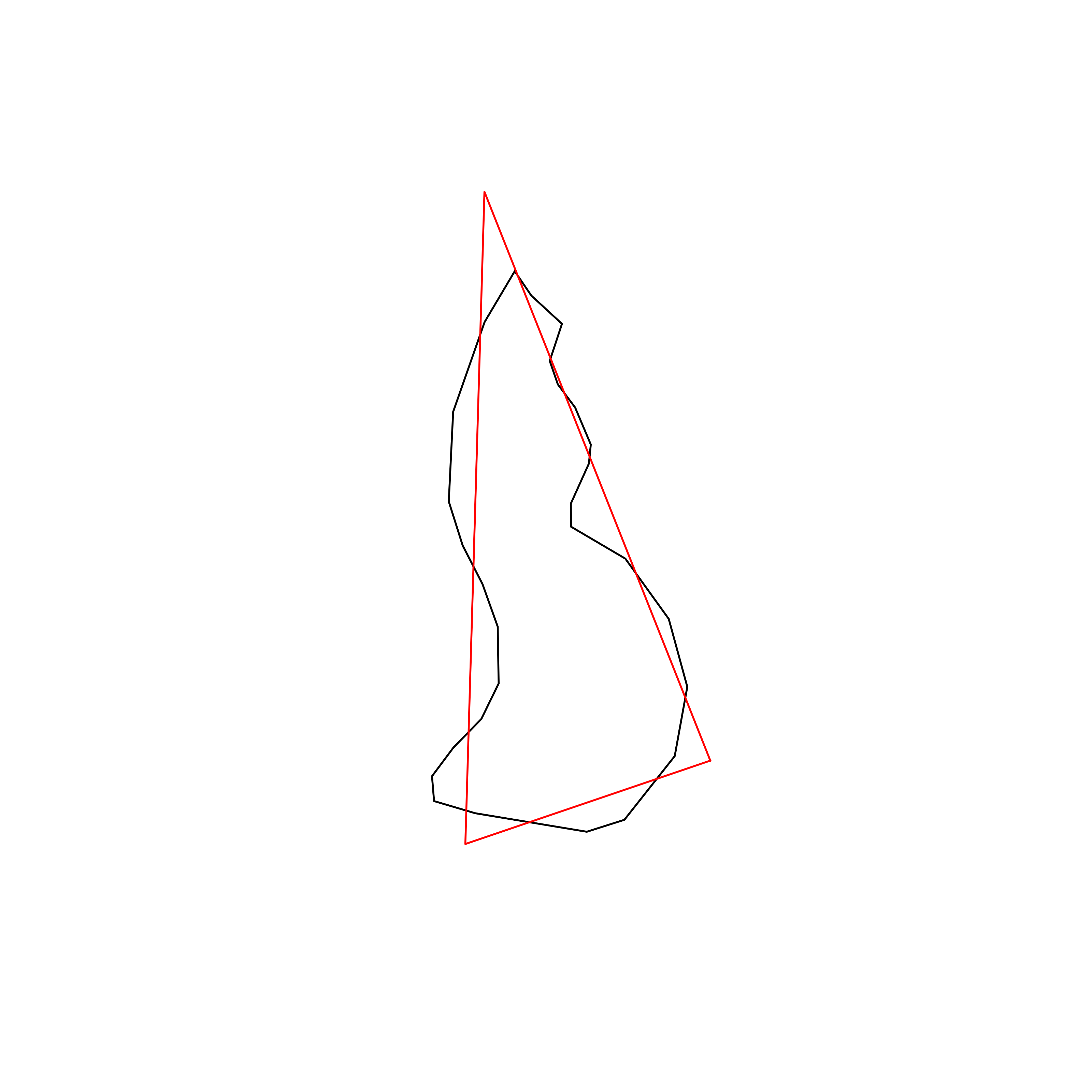 |
| 46 | Afghanistan | 0.863858 | 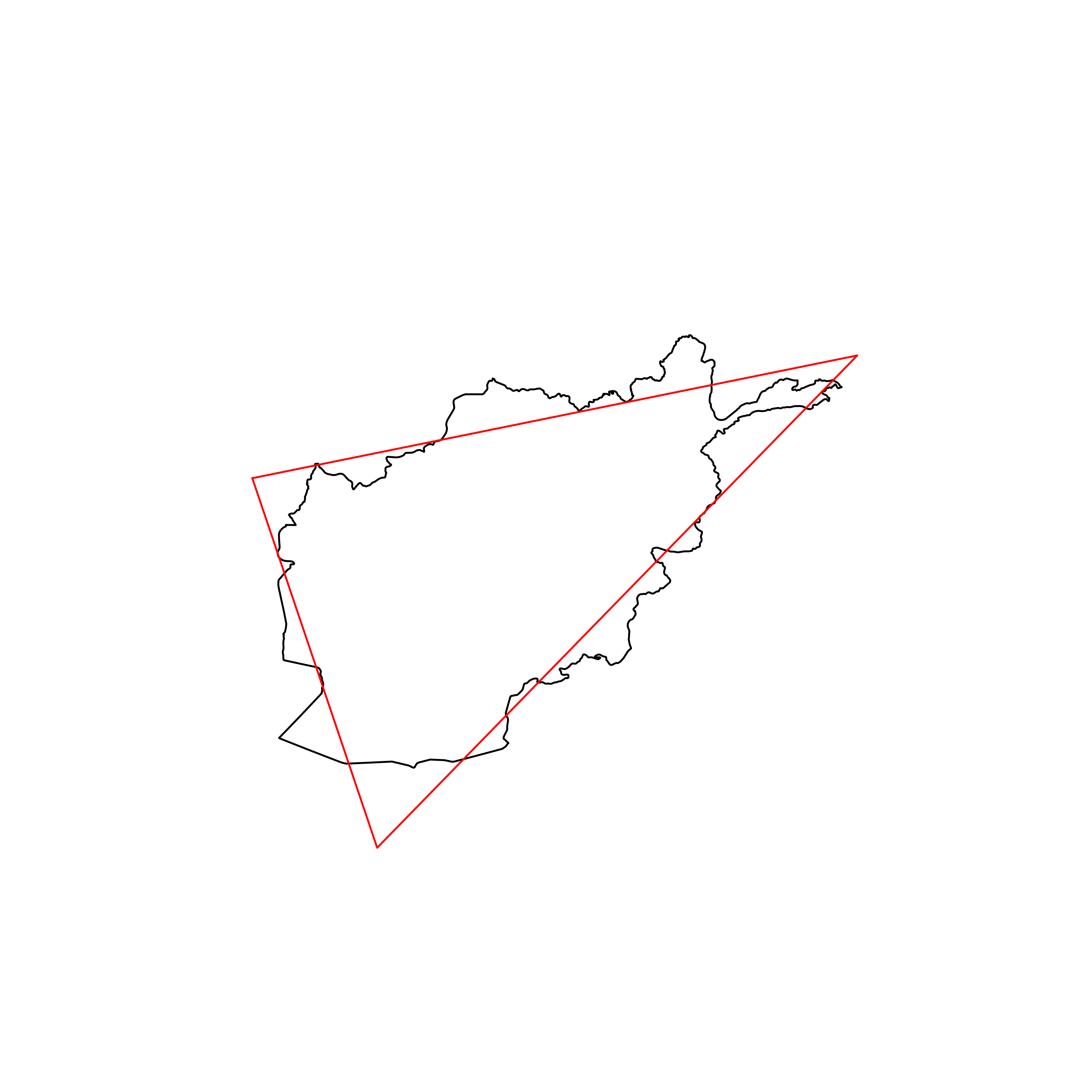 |
| 47 | Honduras | 0.863776 | 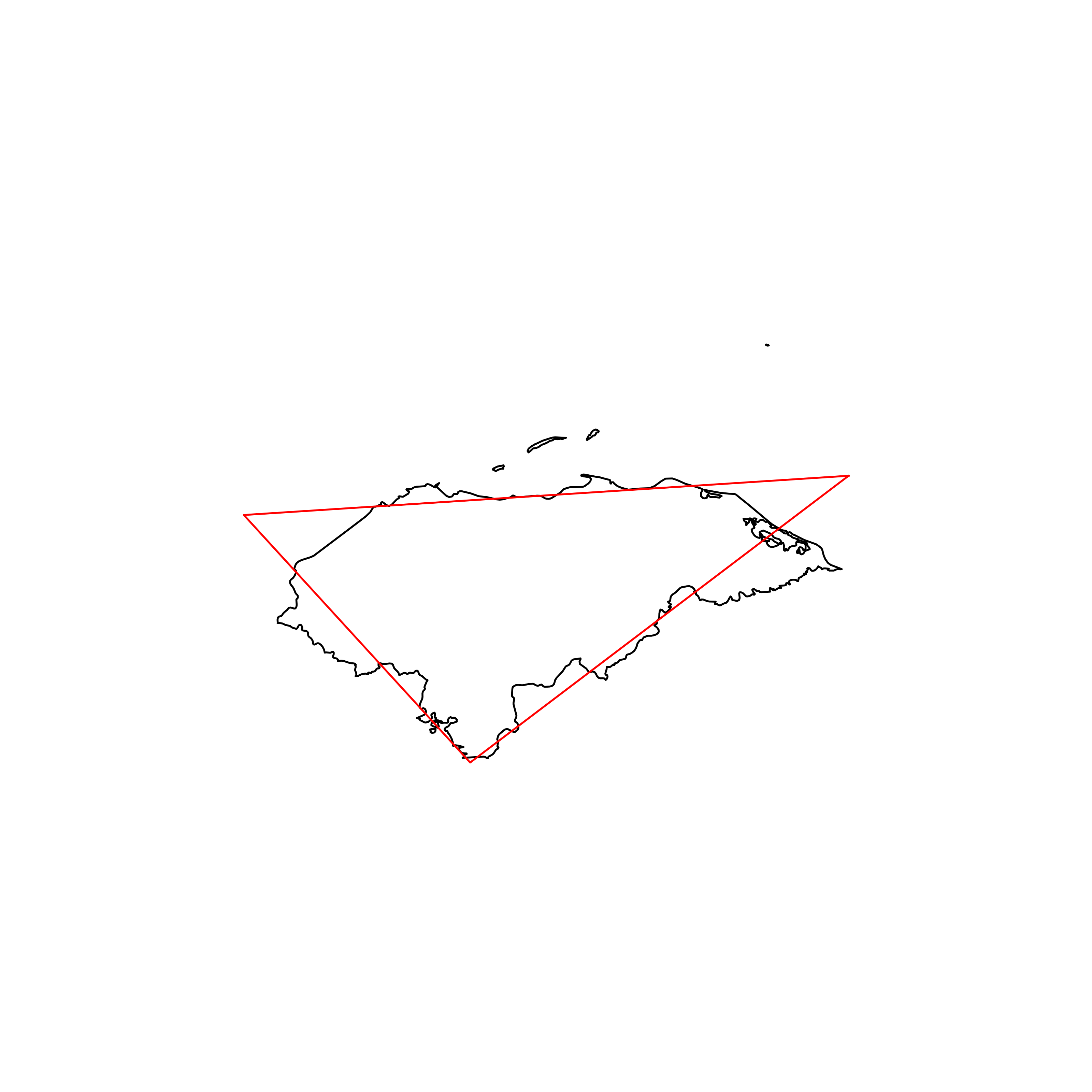 |
| 48 | Burkina Faso | 0.863649 | 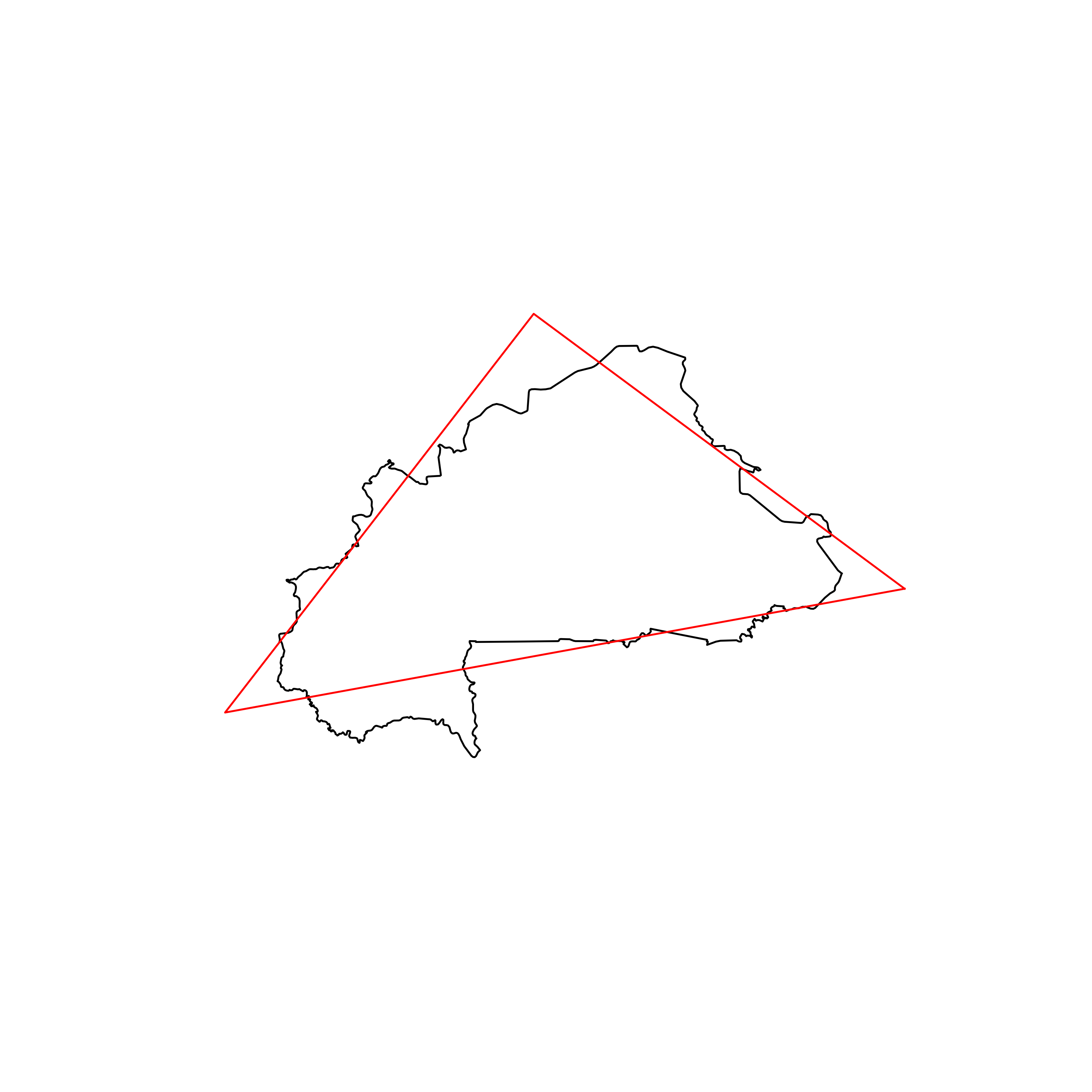 |
| 49 | San Marino | 0.863048 | 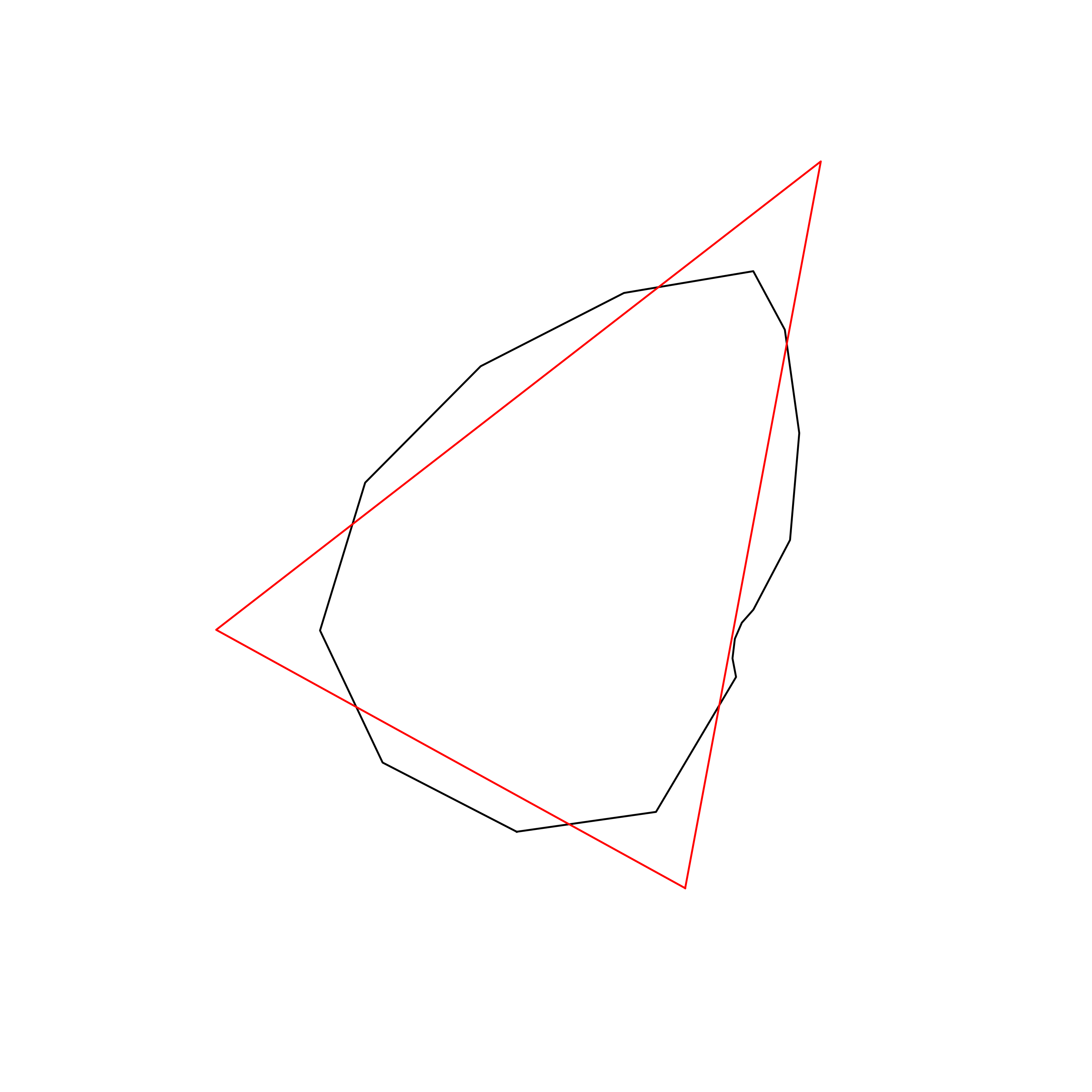 |
| 50 | South Africa | 0.860611 | 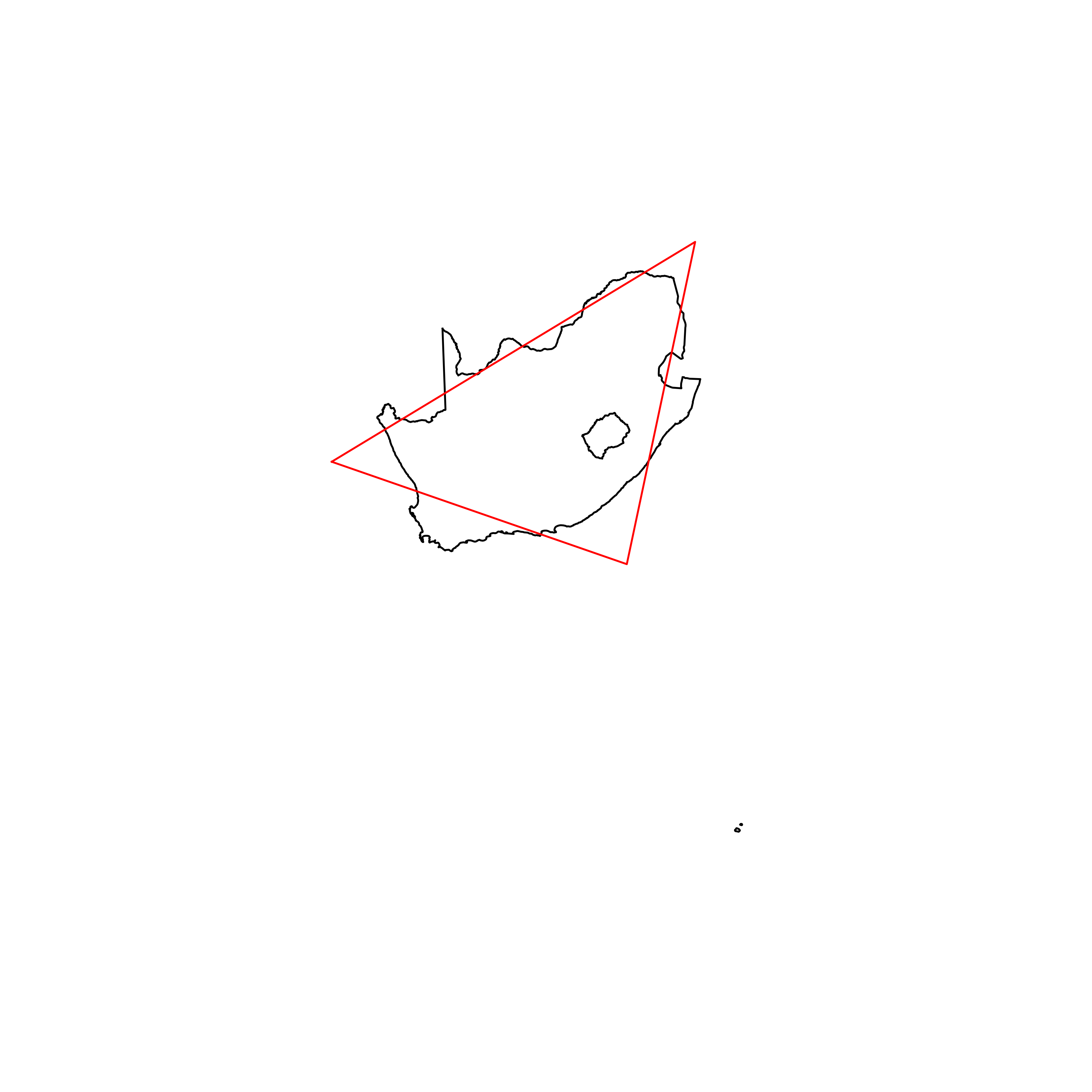 |
| 51 | Vatican | 0.860316 | 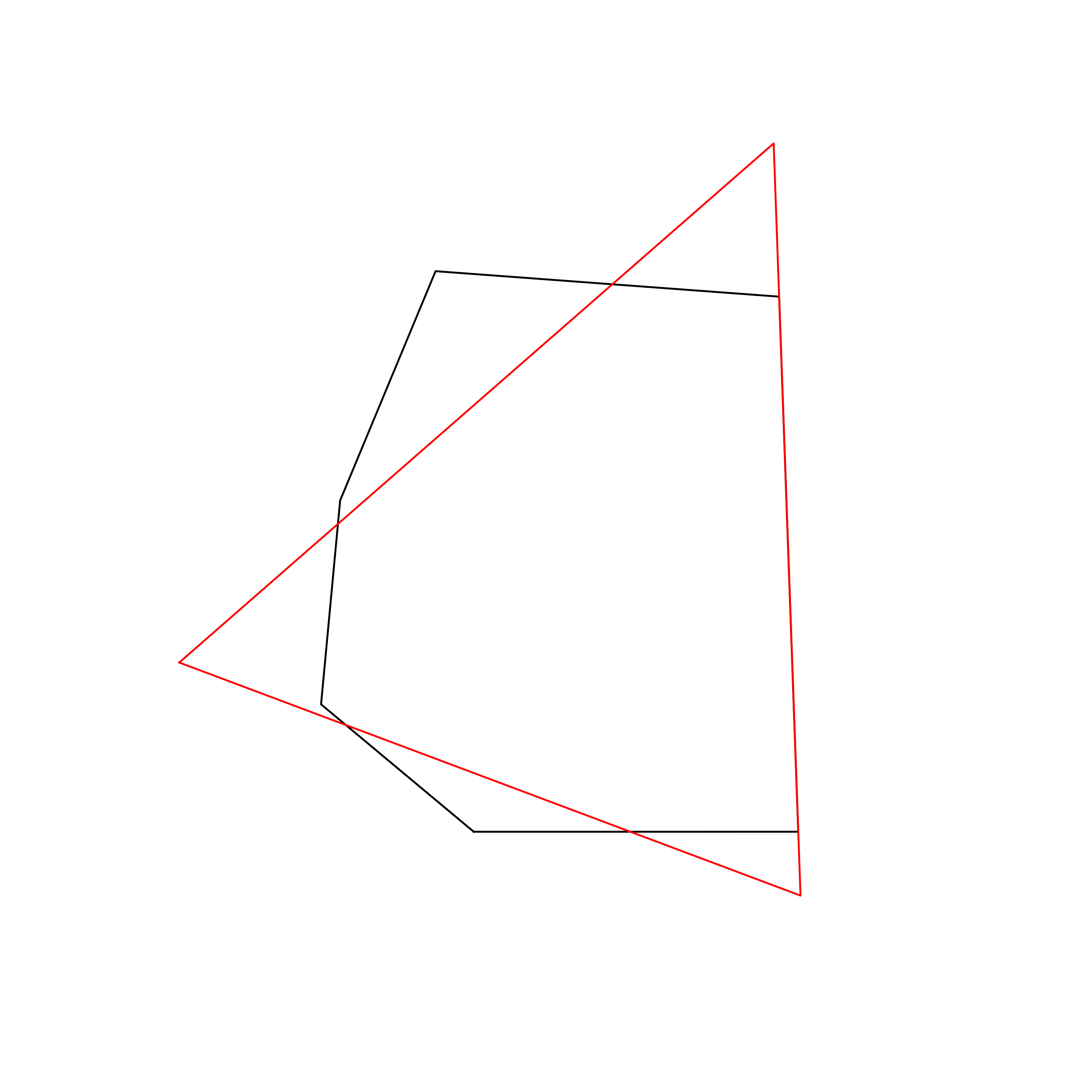 |
| 52 | Belgium | 0.859731 | 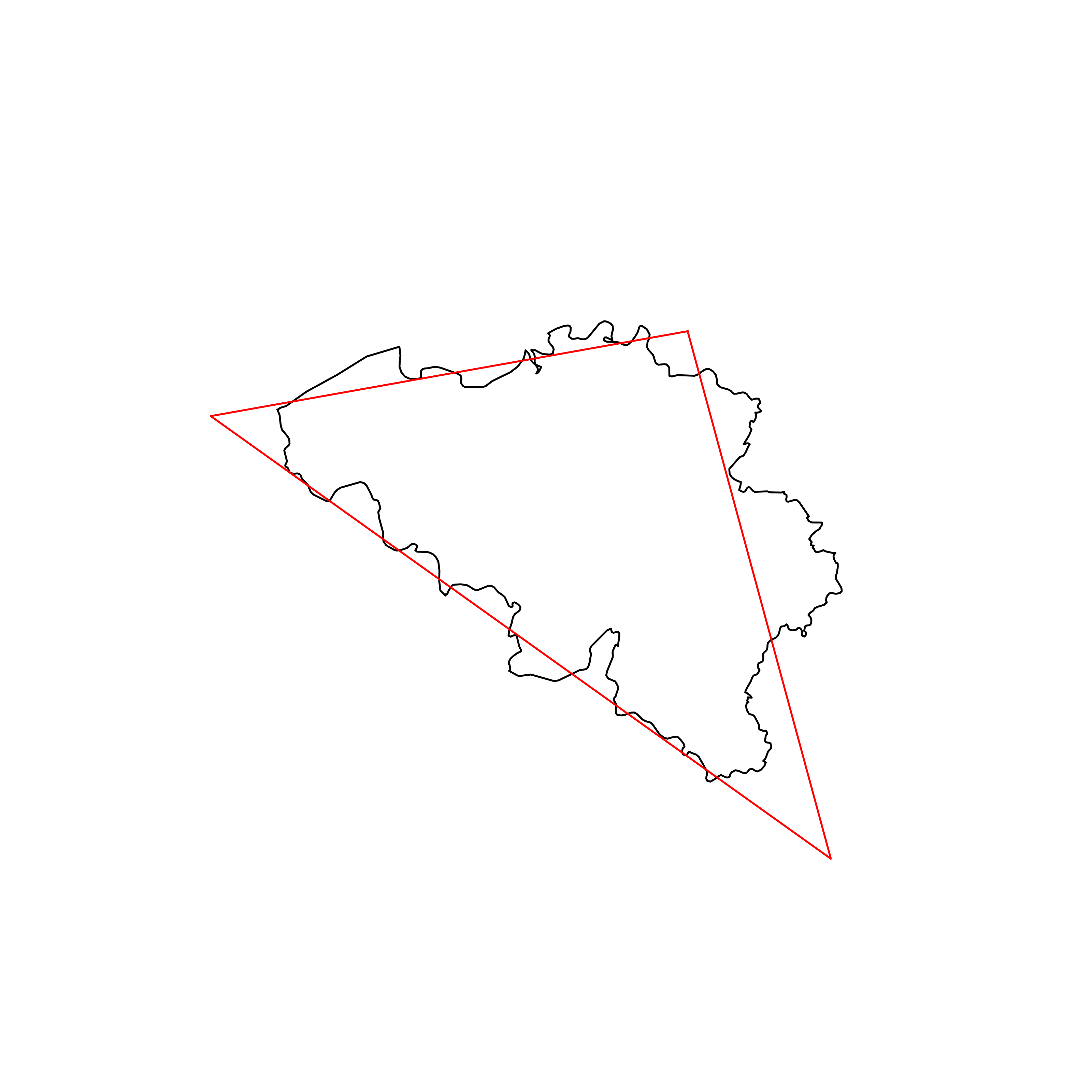 |
| 53 | Poland | 0.859164 | 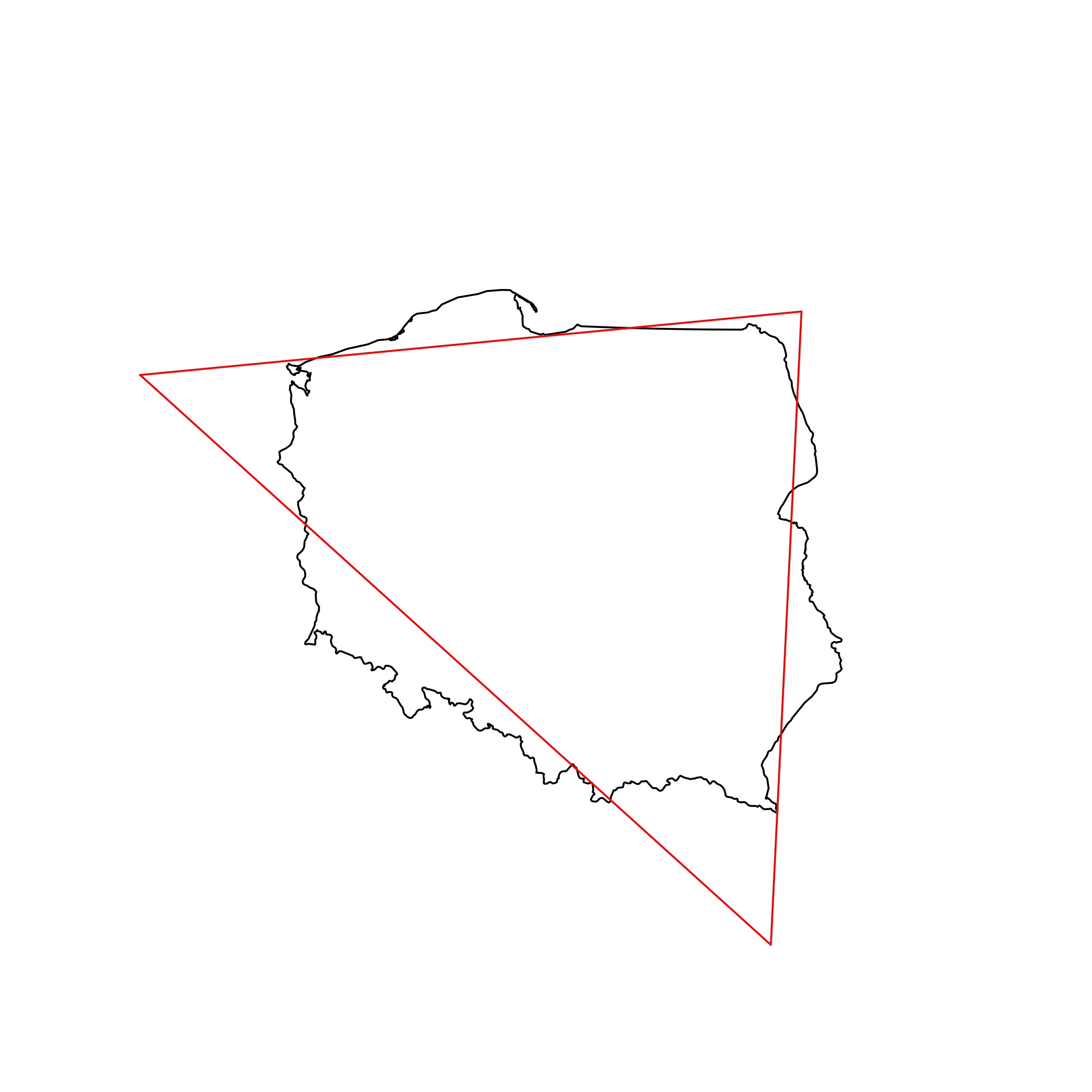 |
| 54 | Georgia | 0.859137 | 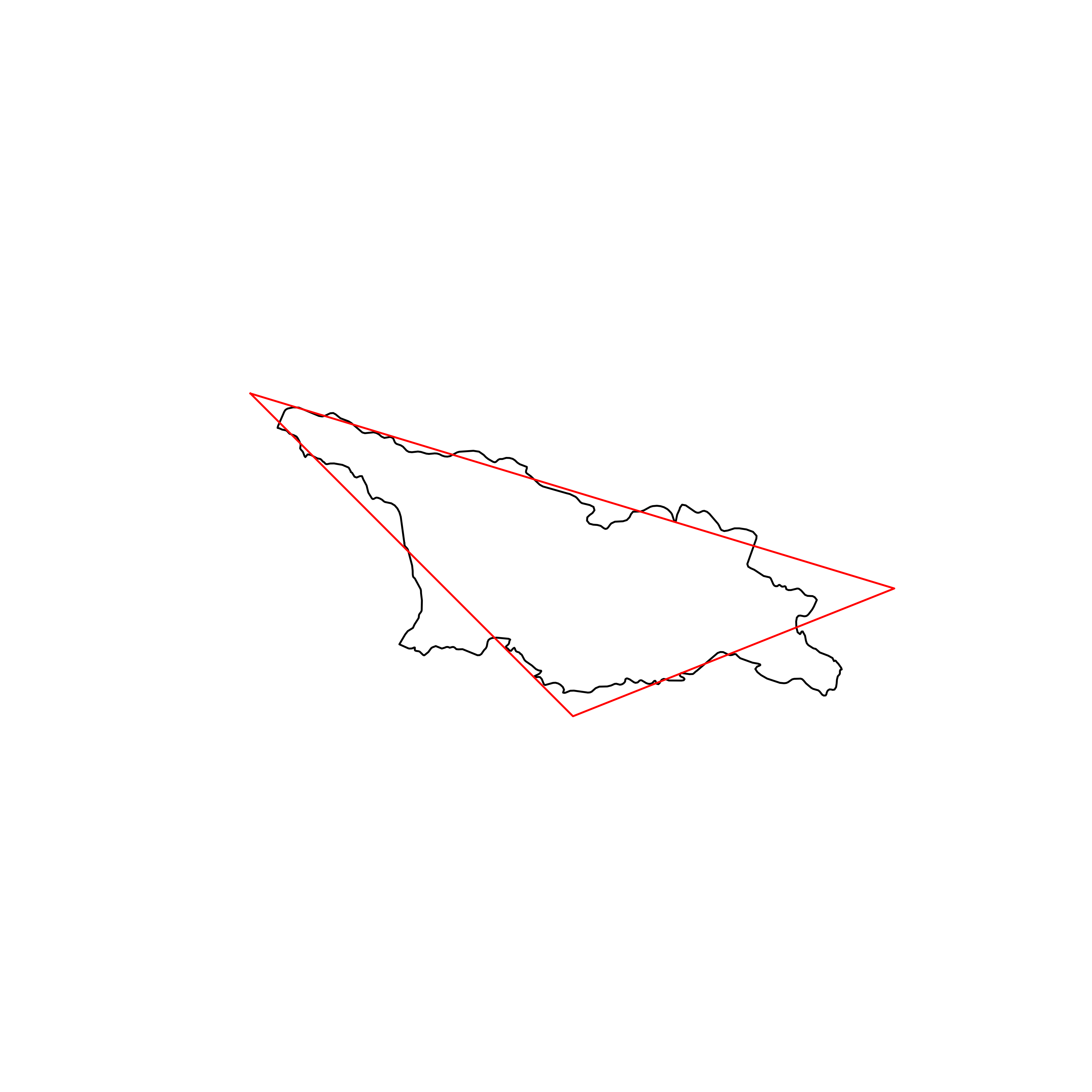 |
| 55 | Austria | 0.858090 | 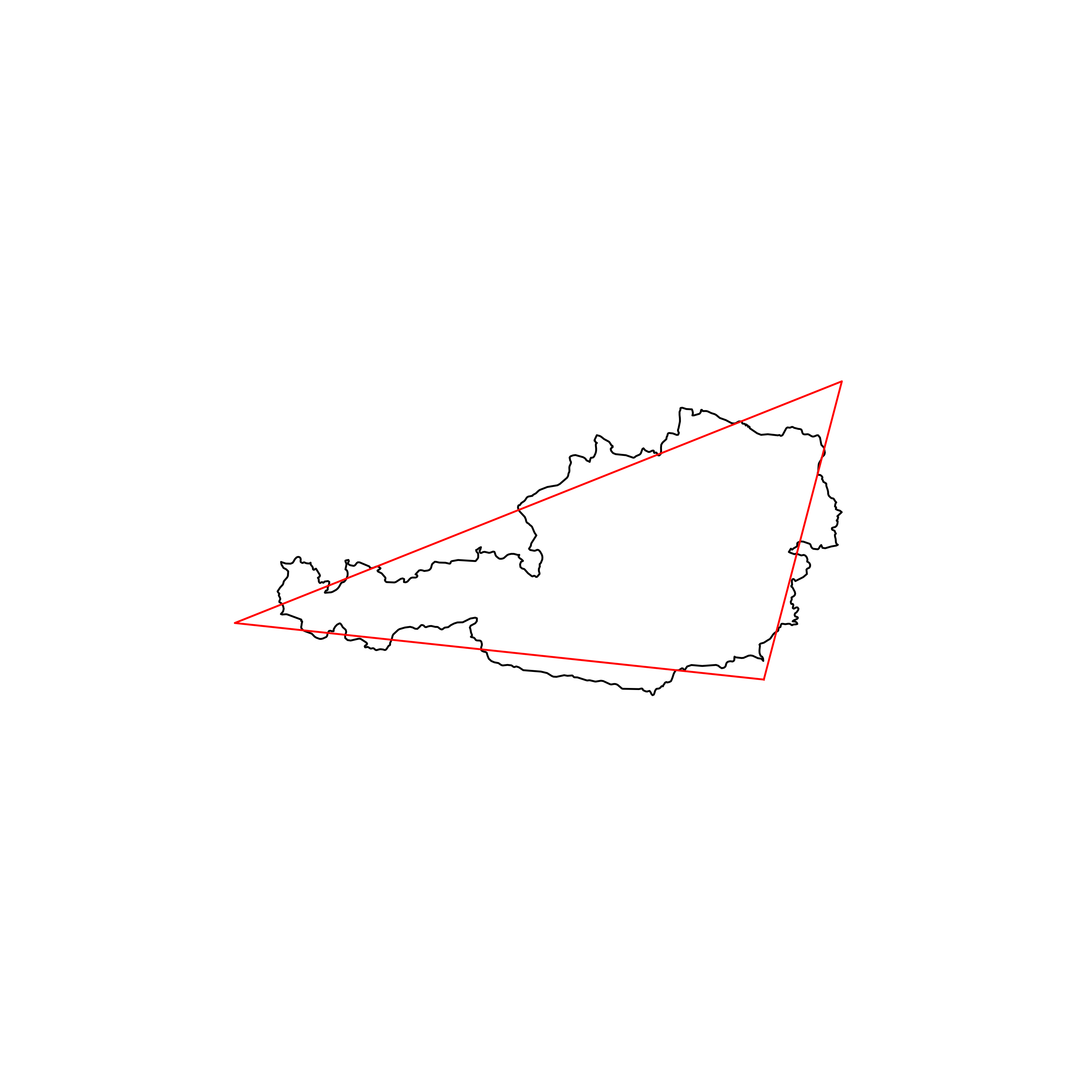 |
| 56 | Hungary | 0.857817 | 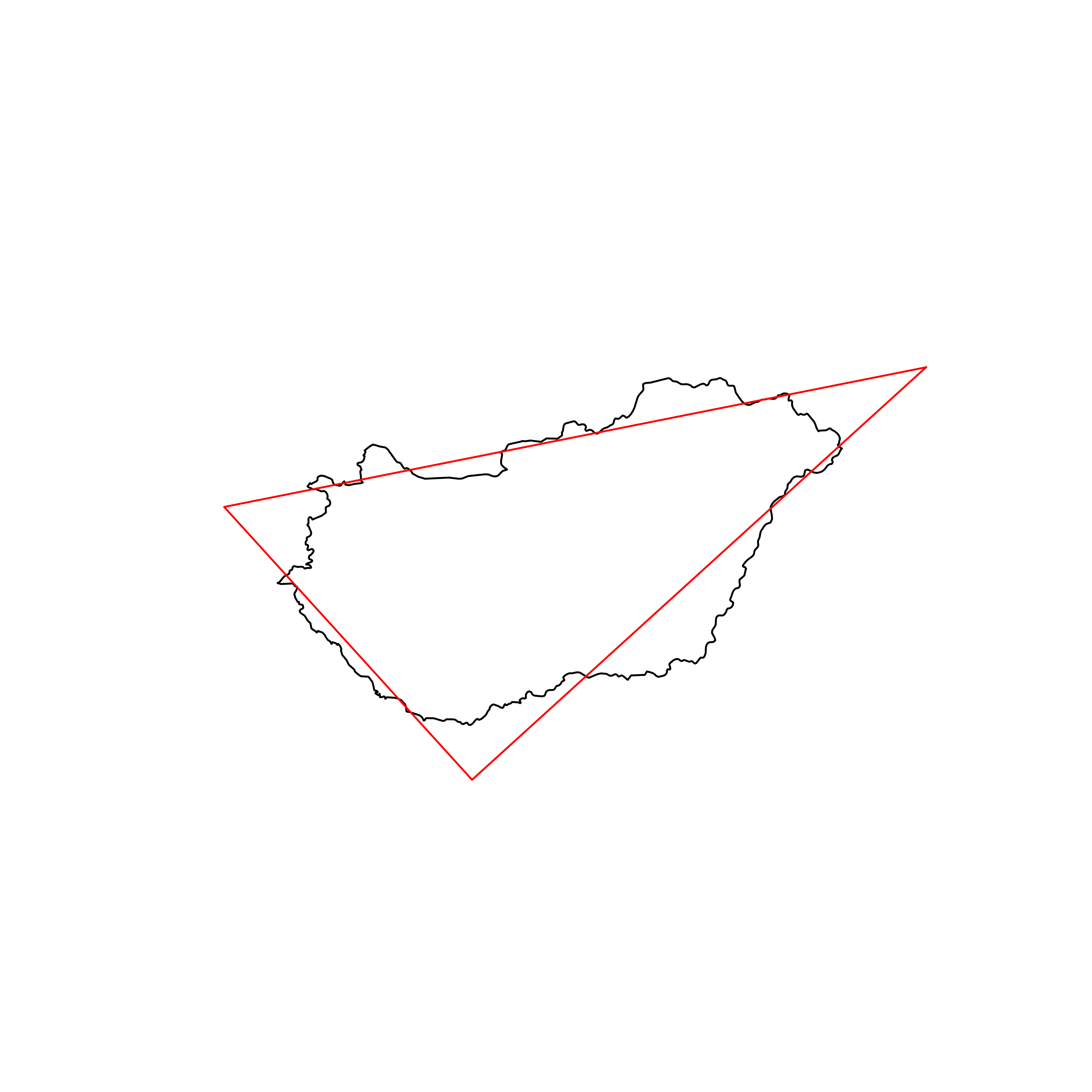 |
| 57 | Ghana | 0.857068 | 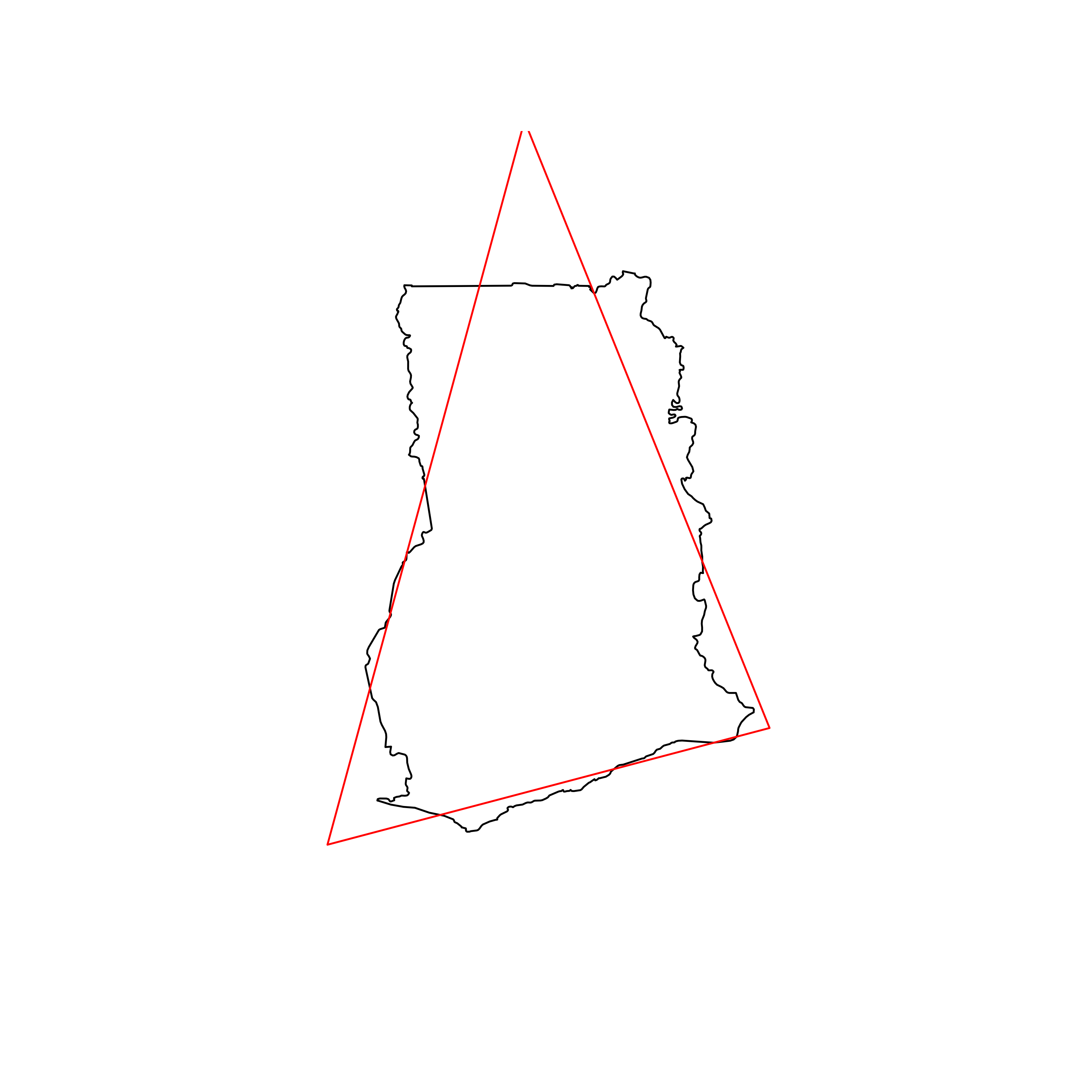 |
| 58 | Nepal | 0.857044 | 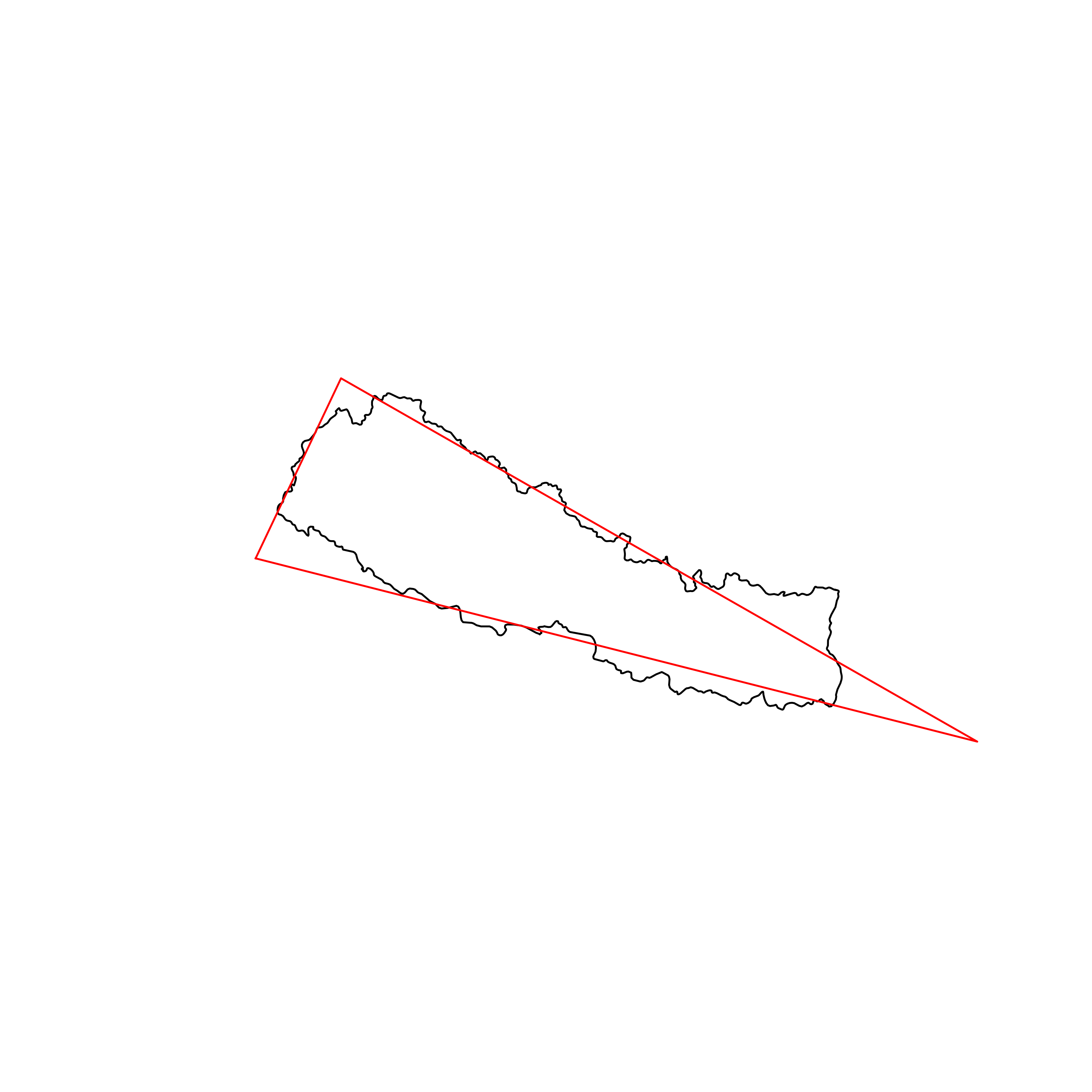 |
| 59 | Slovakia | 0.856166 | 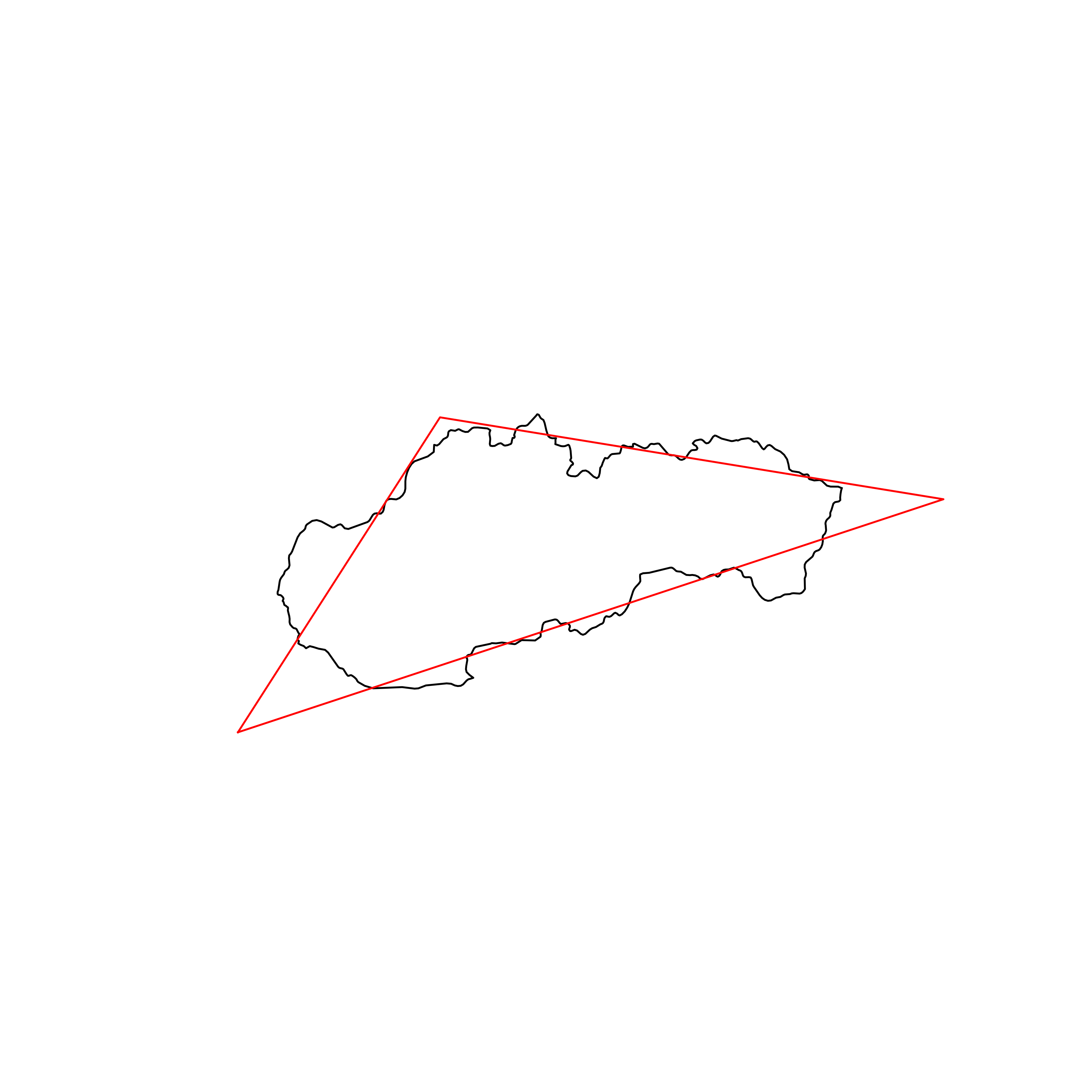 |
| 60 | El Salvador | 0.856155 | 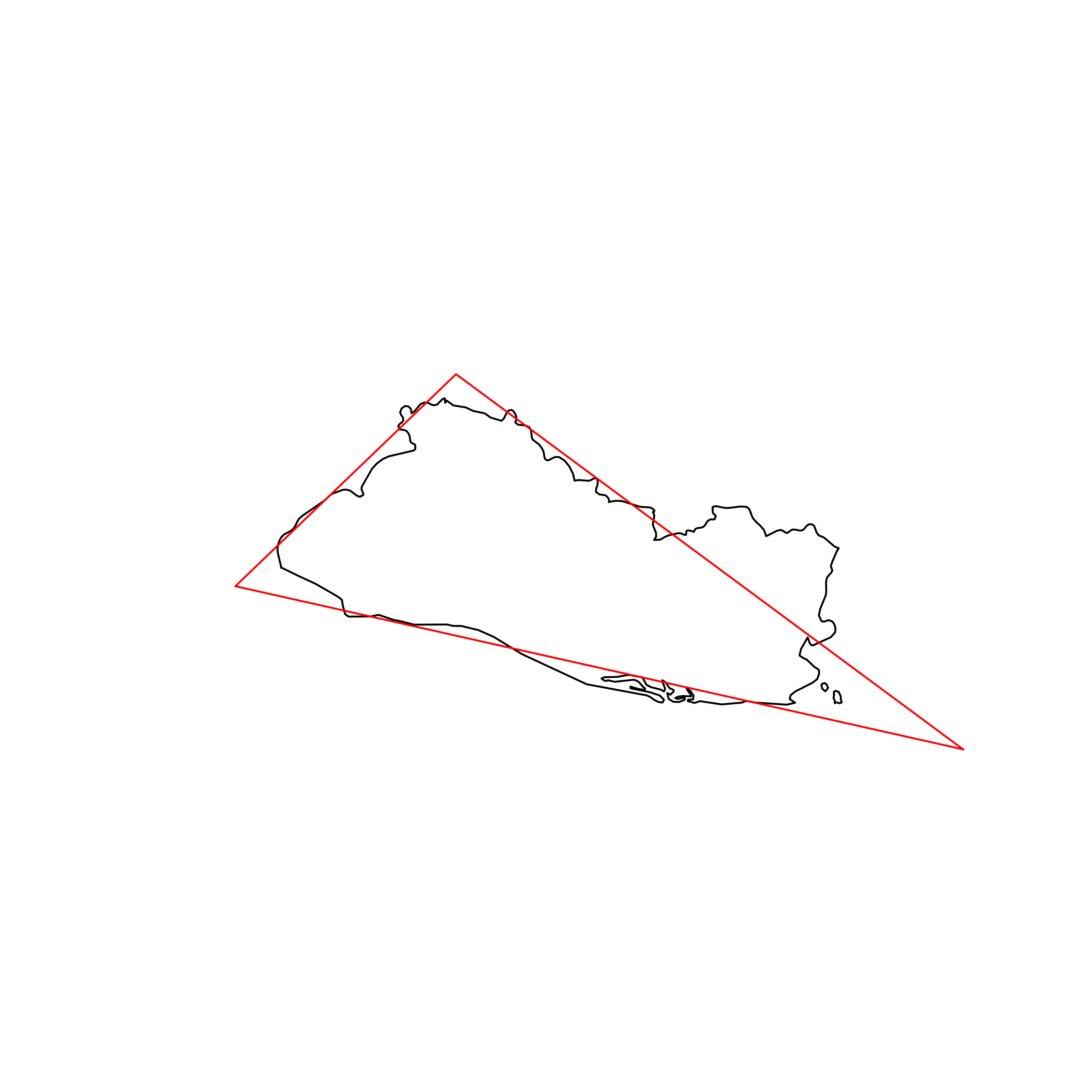 |
| 61 | Republic of Serbia | 0.856100 | 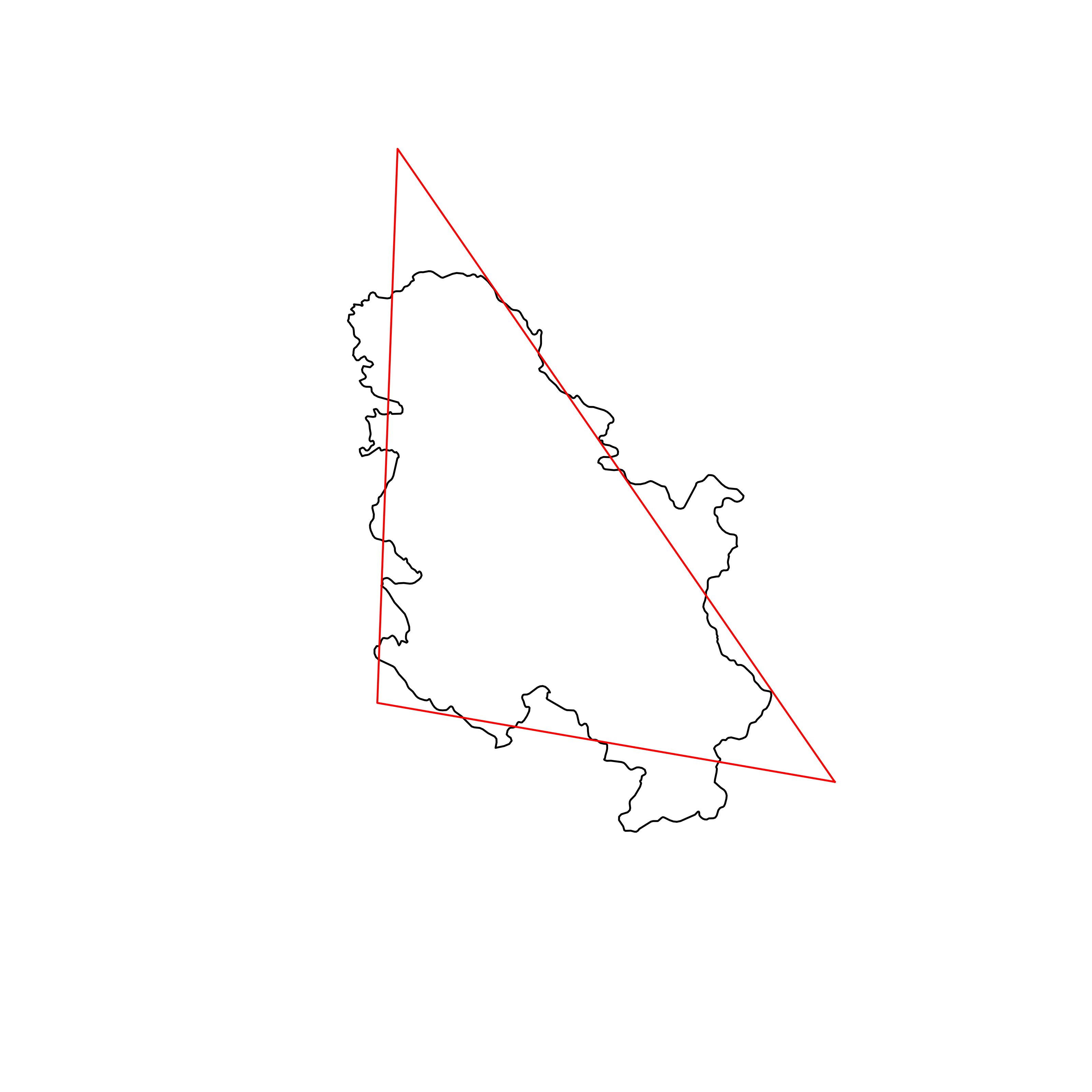 |
| 62 | Armenia | 0.856031 | 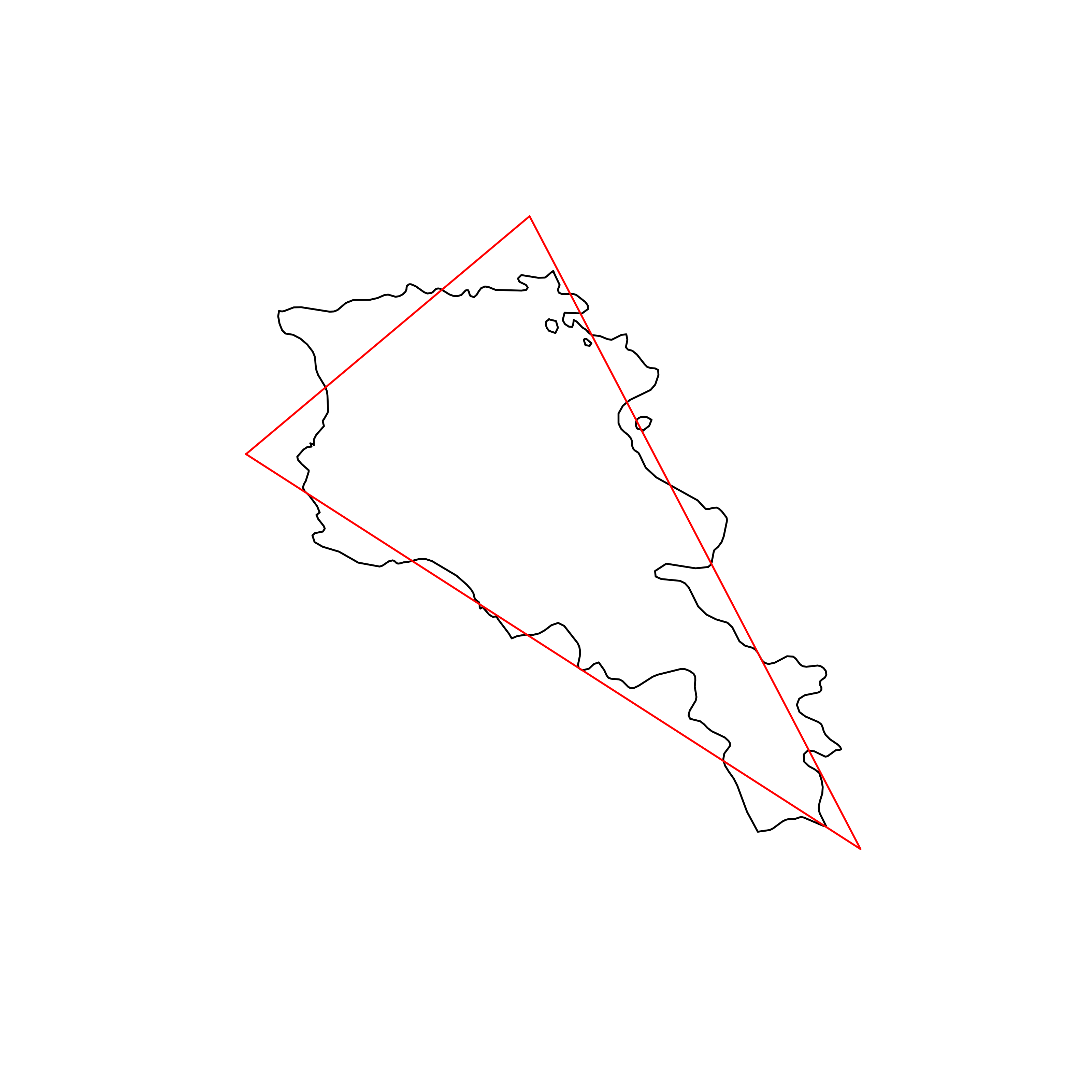 |
| 63 | Morocco | 0.855741 | 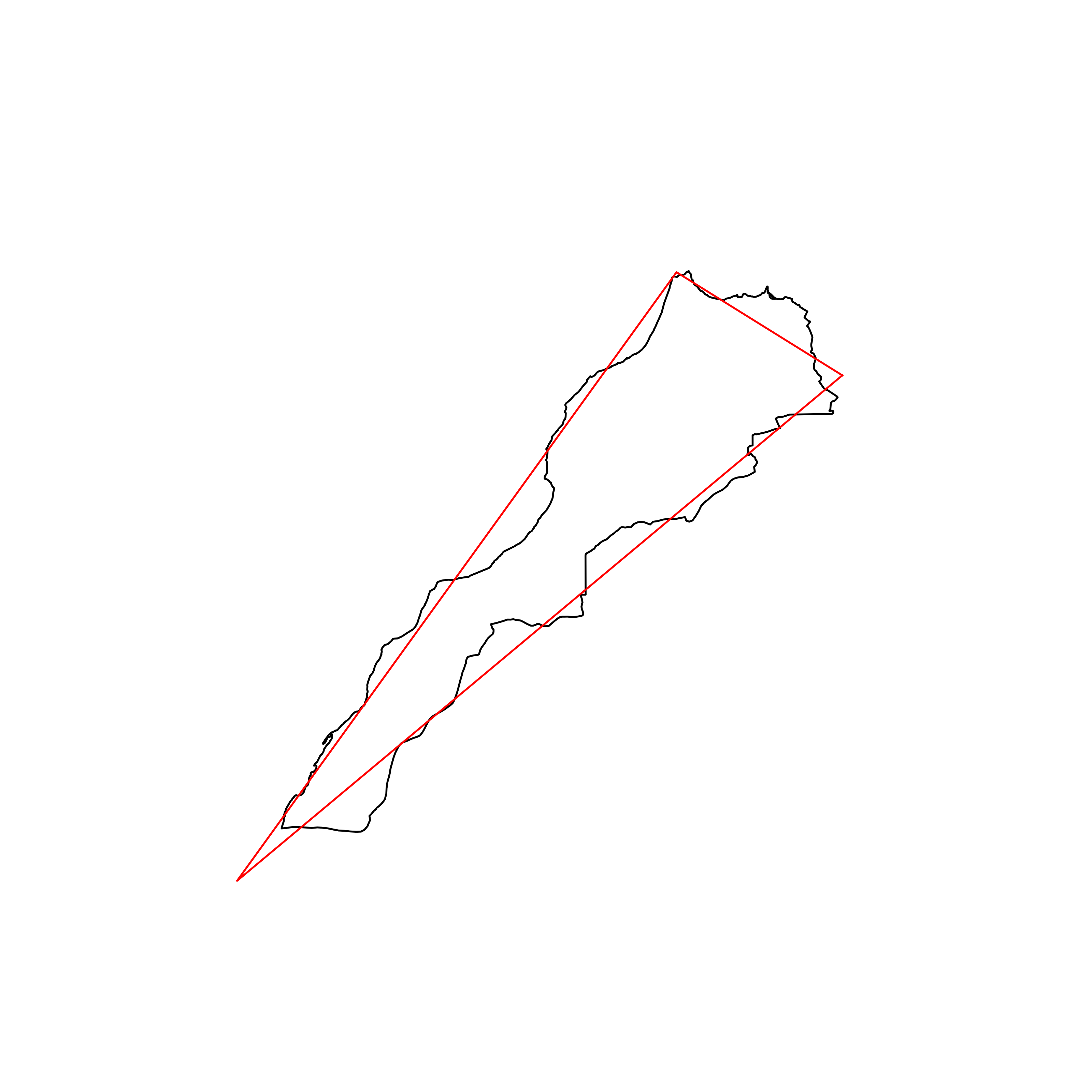 |
| 64 | North Korea | 0.855623 | 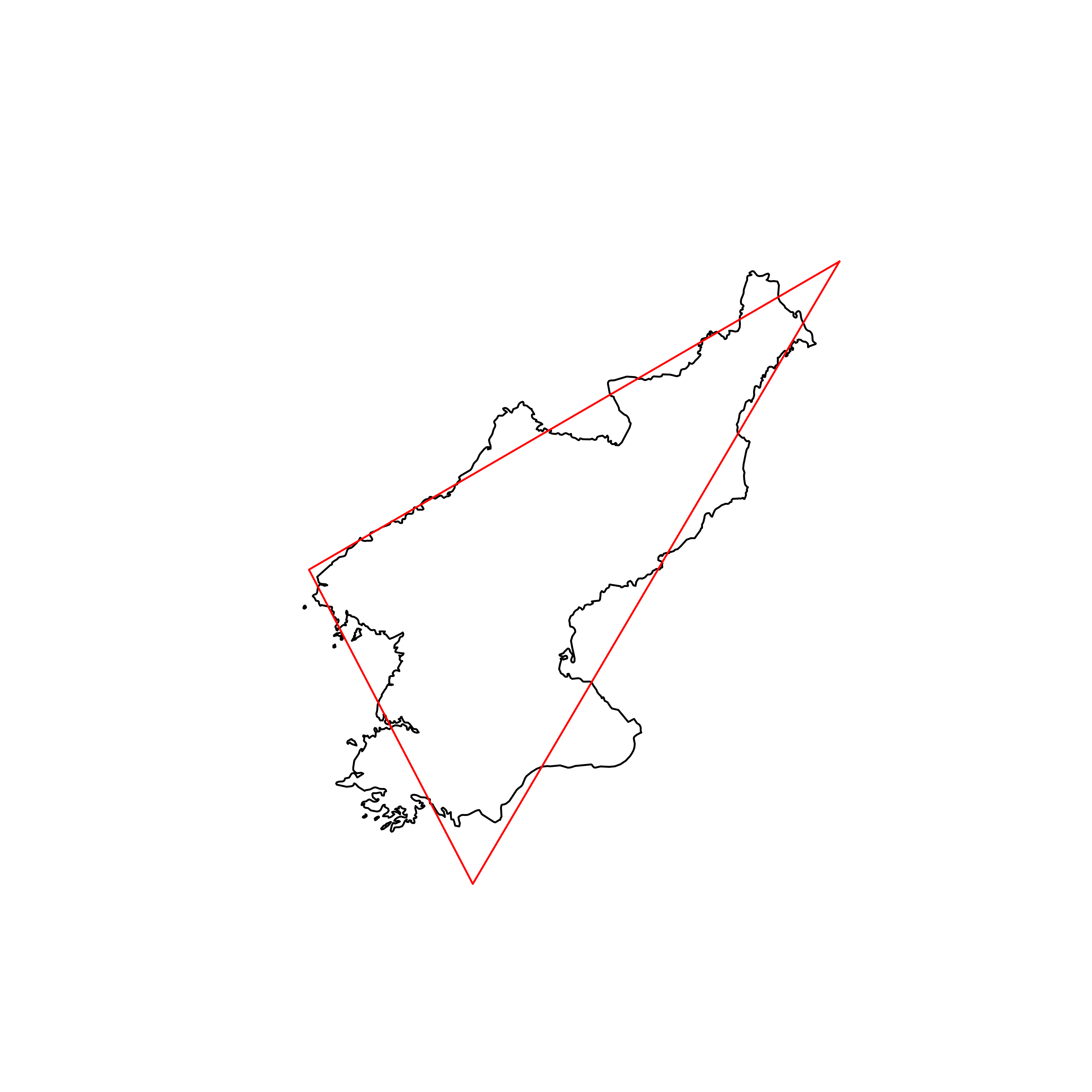 |
| 65 | South Sudan | 0.854143 |  |
| 66 | Estonia | 0.853185 |  |
| 67 | Yemen | 0.852291 |  |
| 68 | Mauritius | 0.852287 |  |
| 69 | Burundi | 0.852197 |  |
| 70 | Cameroon | 0.852041 |  |
| 71 | Kuwait | 0.852006 | 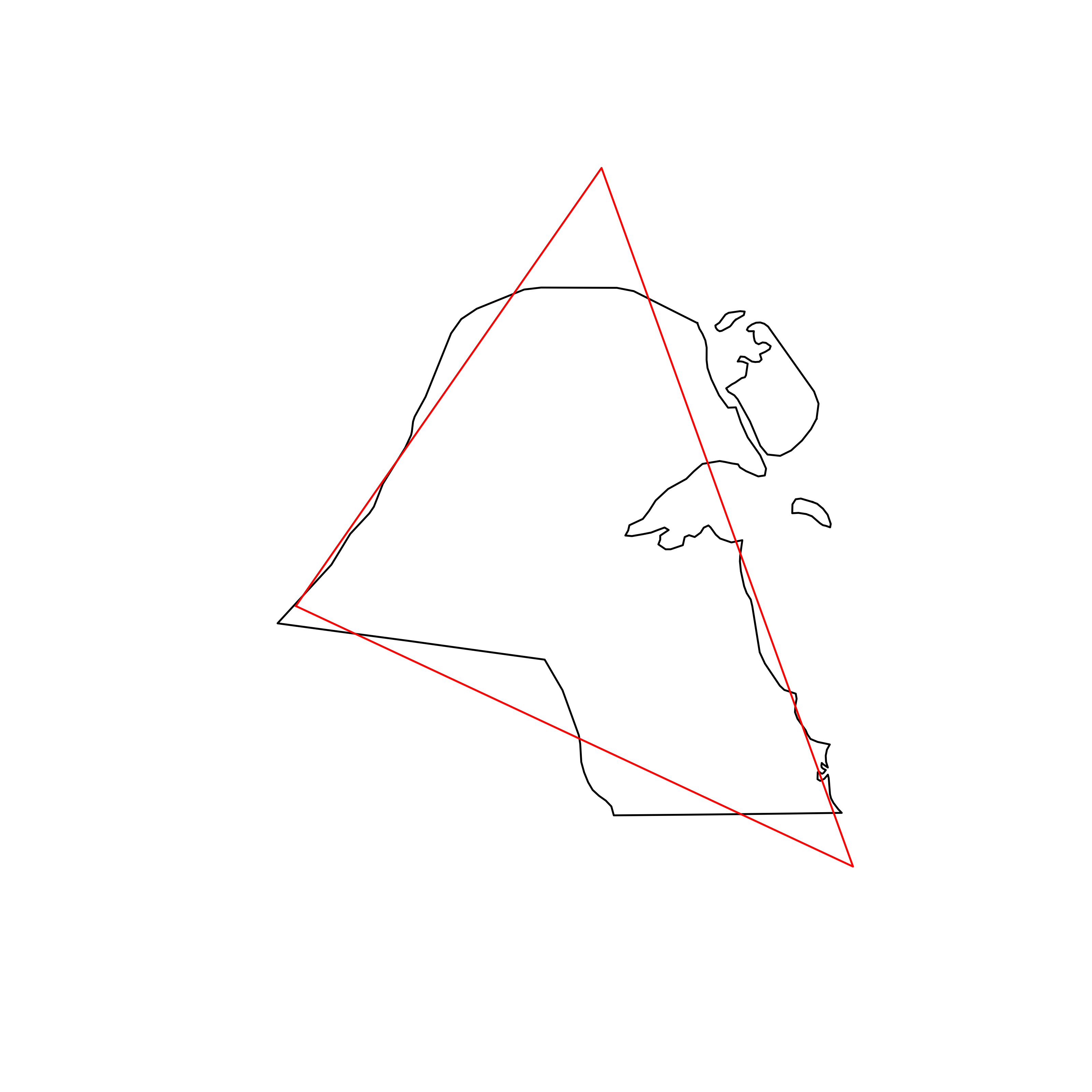 |
| 72 | Luxembourg | 0.851825 | 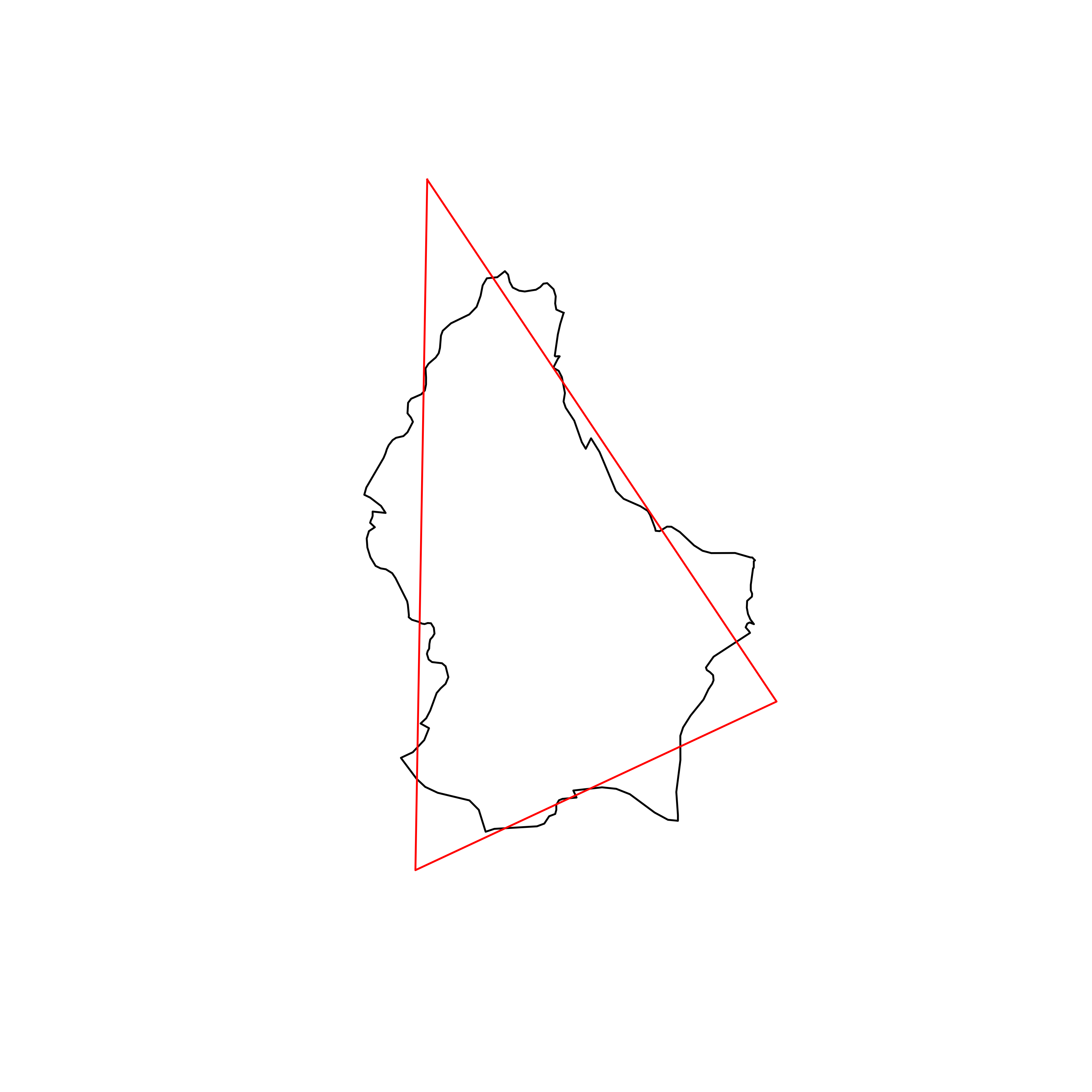 |
| 73 | United Republic of Tanzania | 0.850960 | 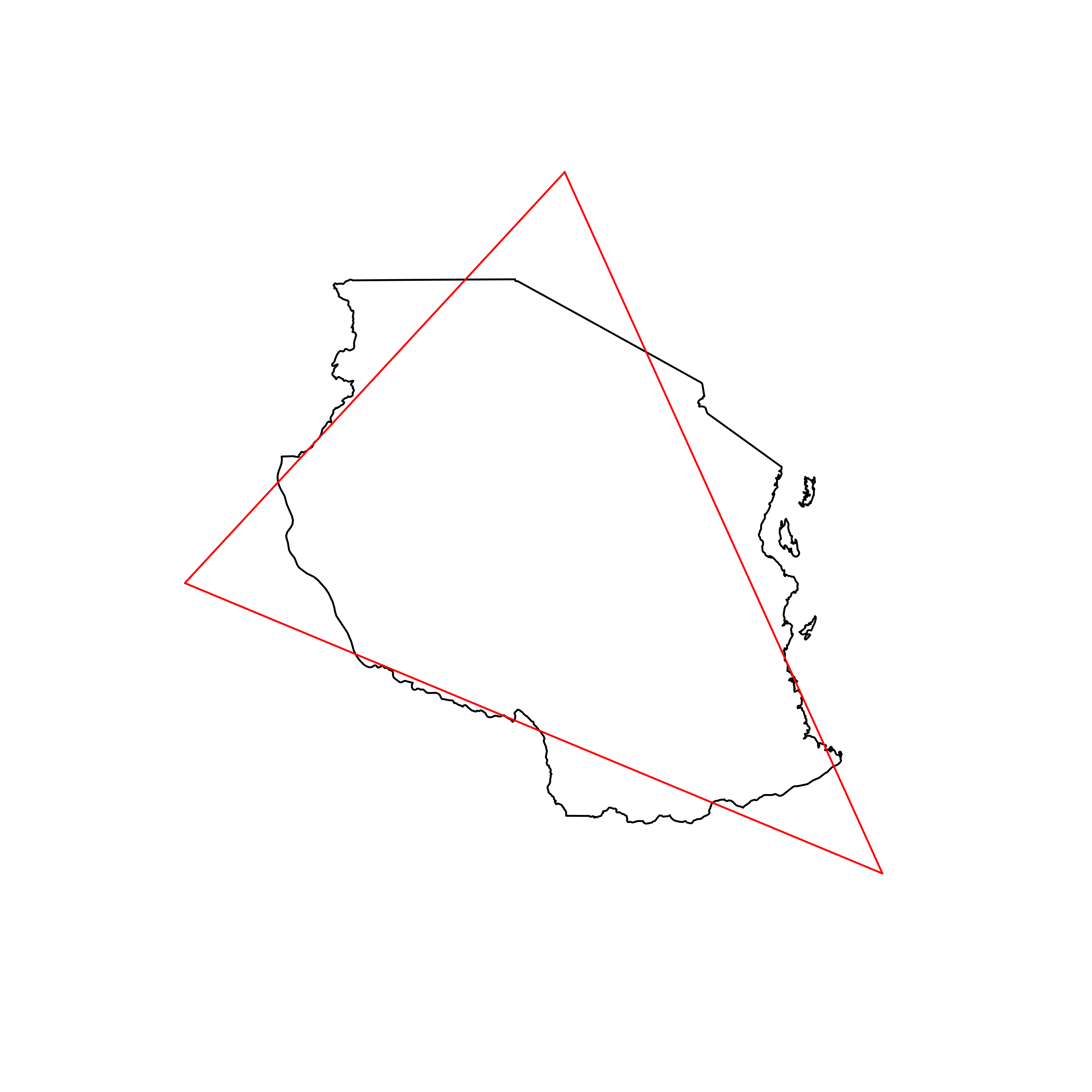 |
| 74 | Monaco | 0.850811 | 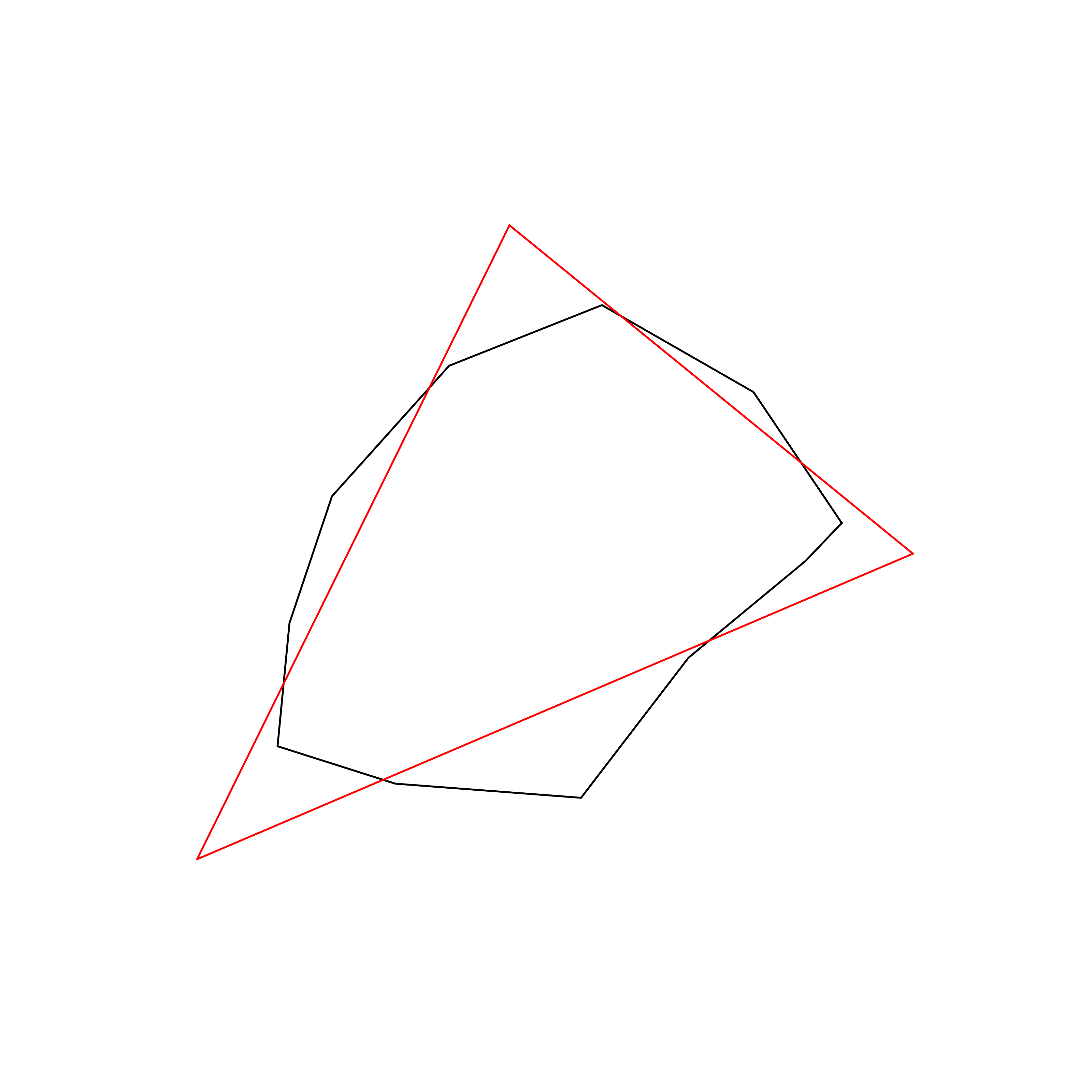 |
| 75 | Kyrgyzstan | 0.849767 | 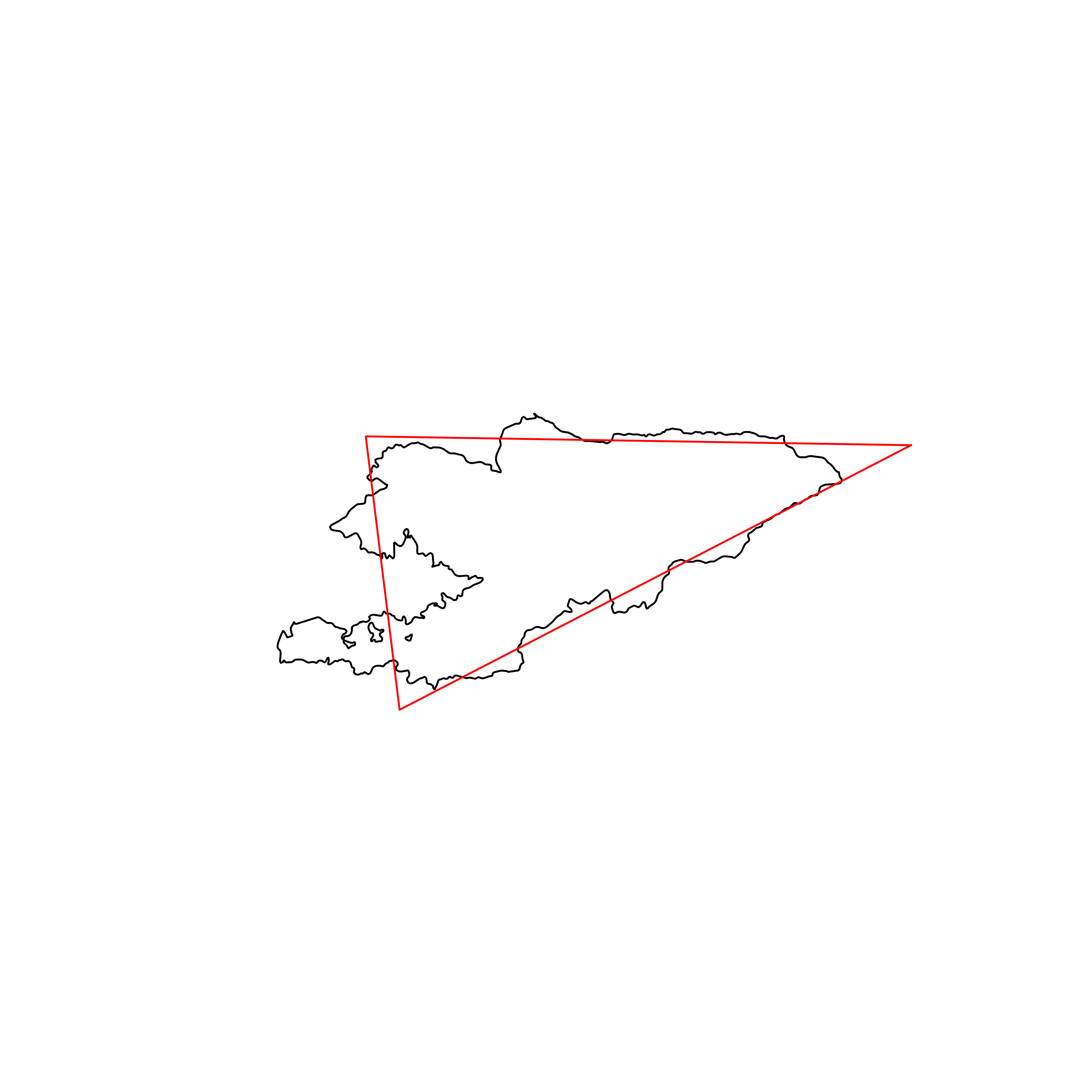 |
| 76 | Ivory Coast | 0.849450 | 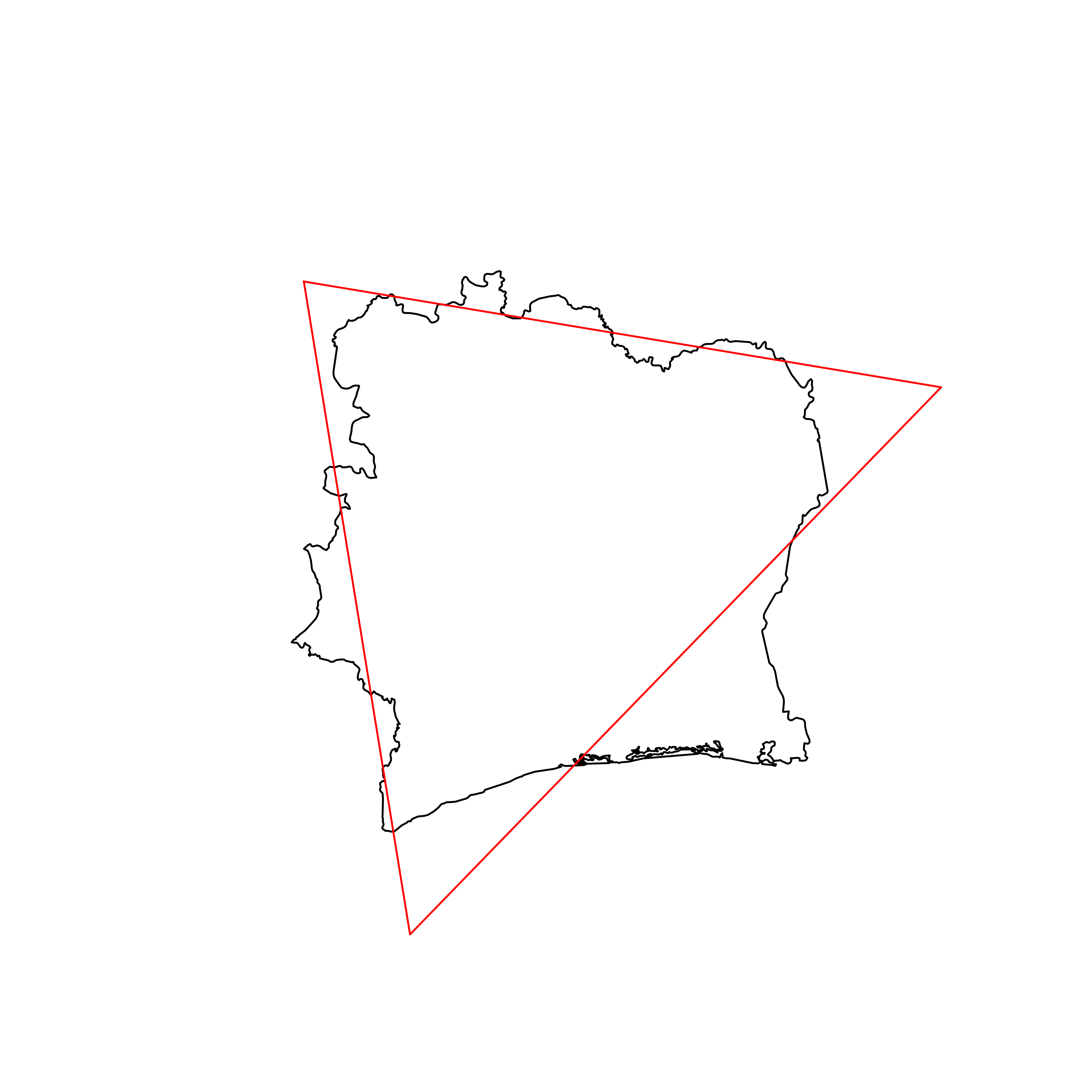 |
| 77 | Guinea | 0.849425 | 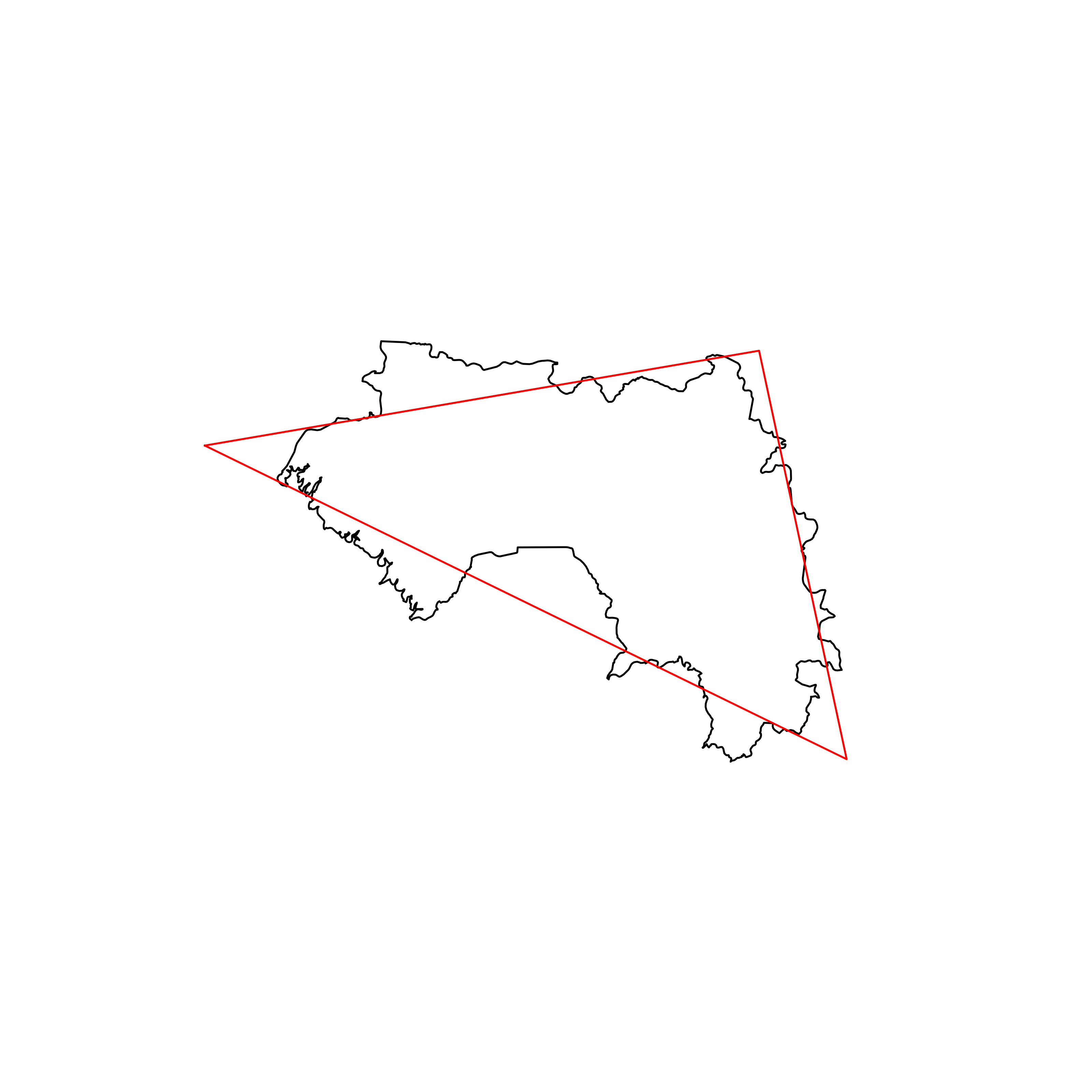 |
| 78 | Romania | 0.849085 | 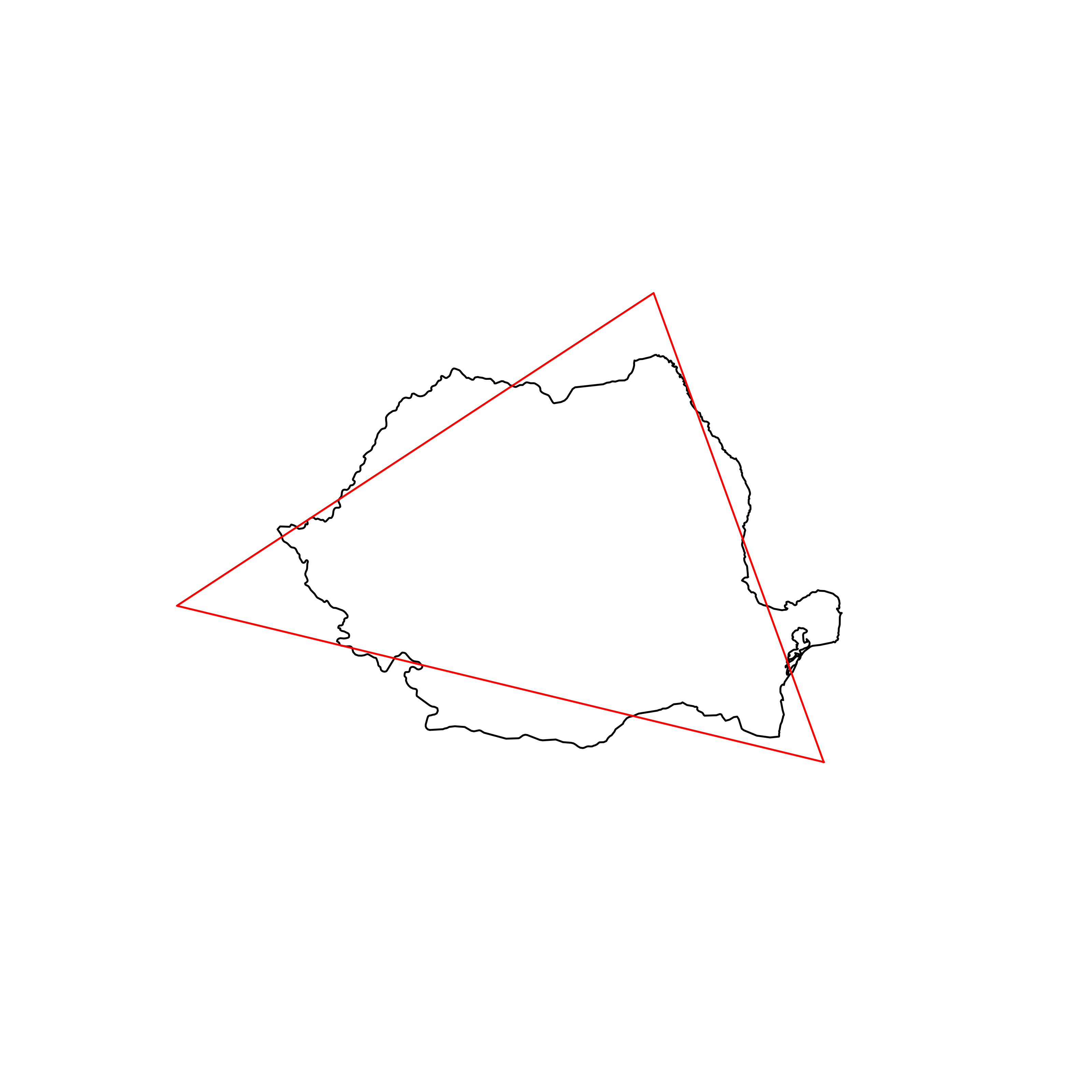 |
| 79 | South Korea | 0.847823 | 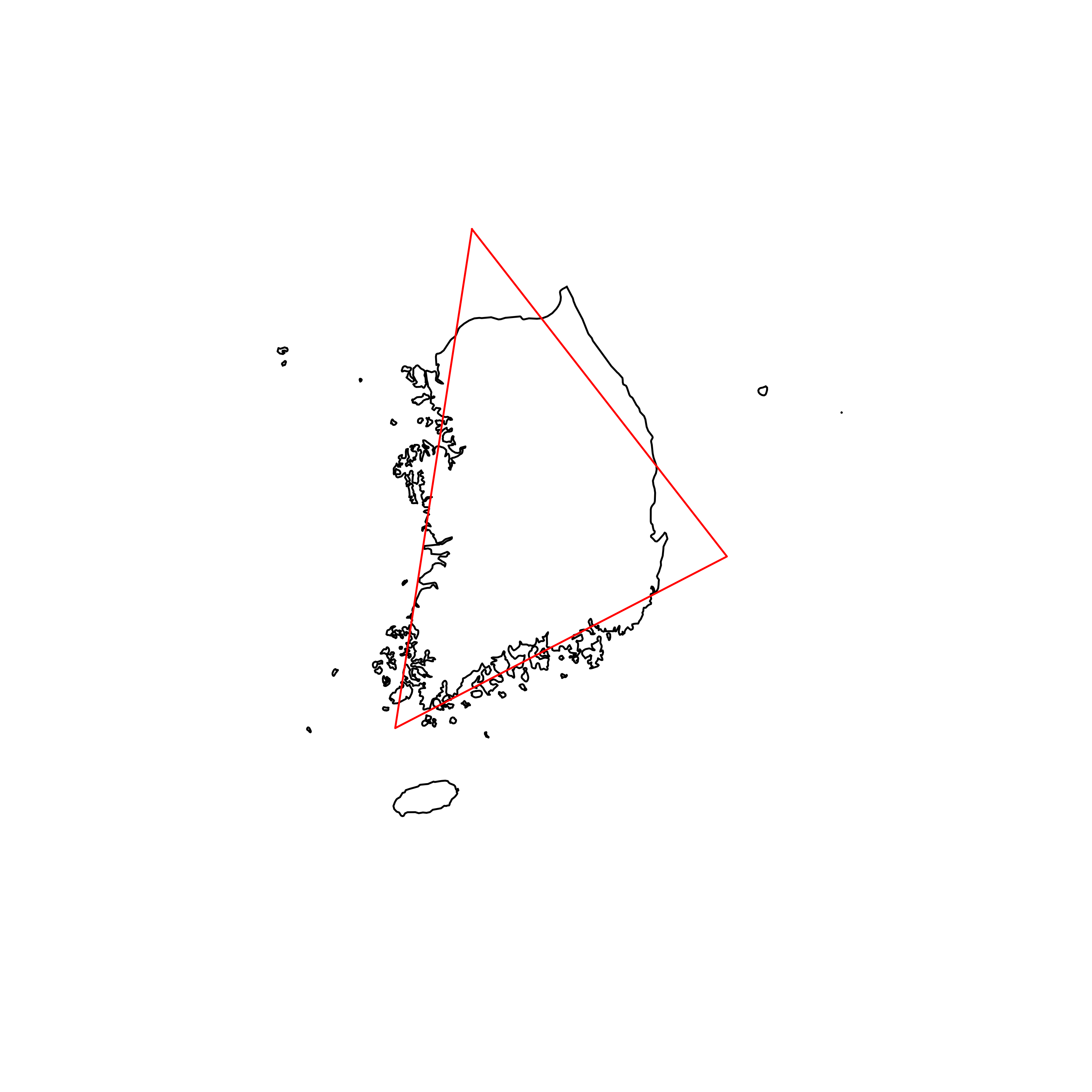 |
| 80 | Uganda | 0.847599 |  |
| 81 | Singapore | 0.847415 | 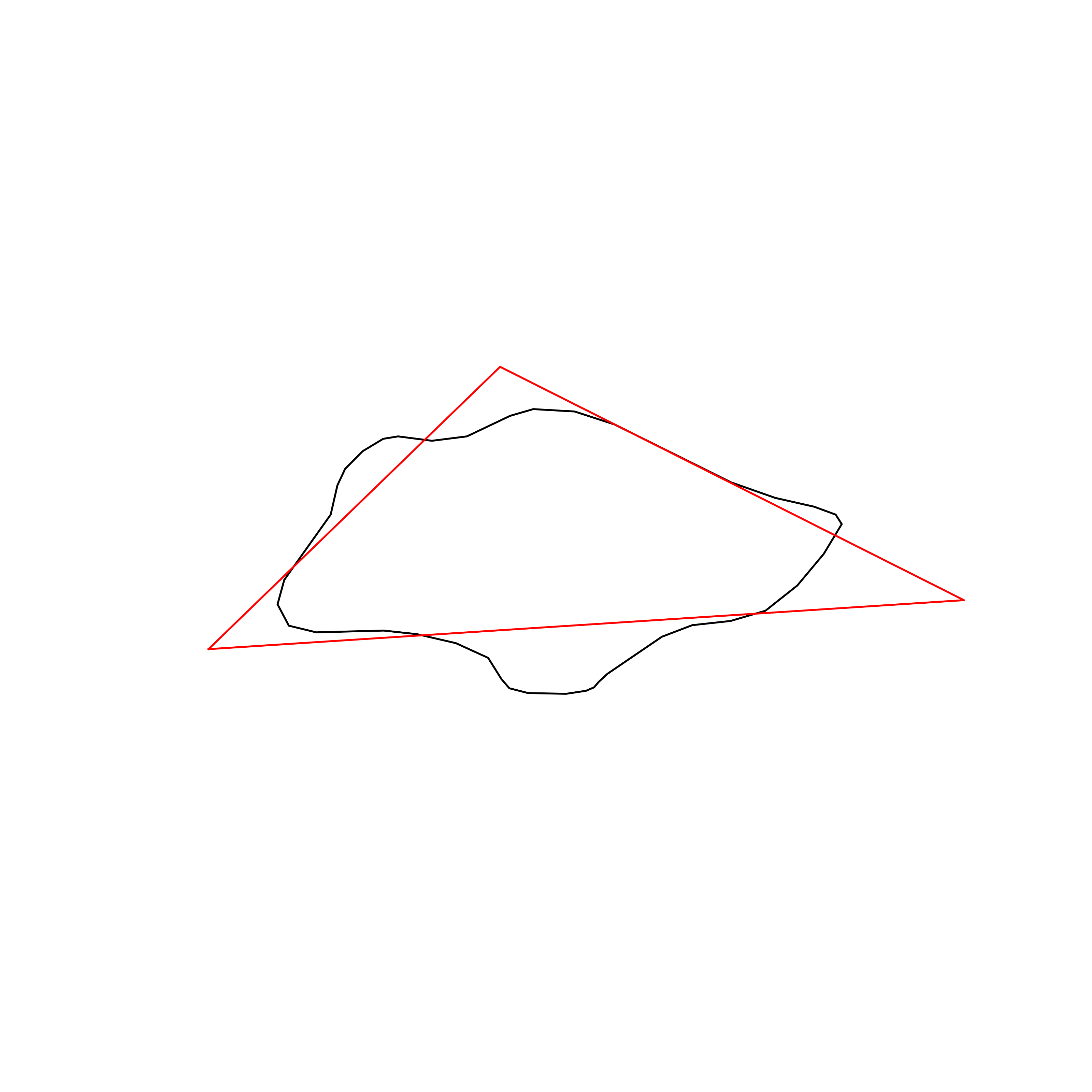 |
| 82 | Kenya | 0.847016 | 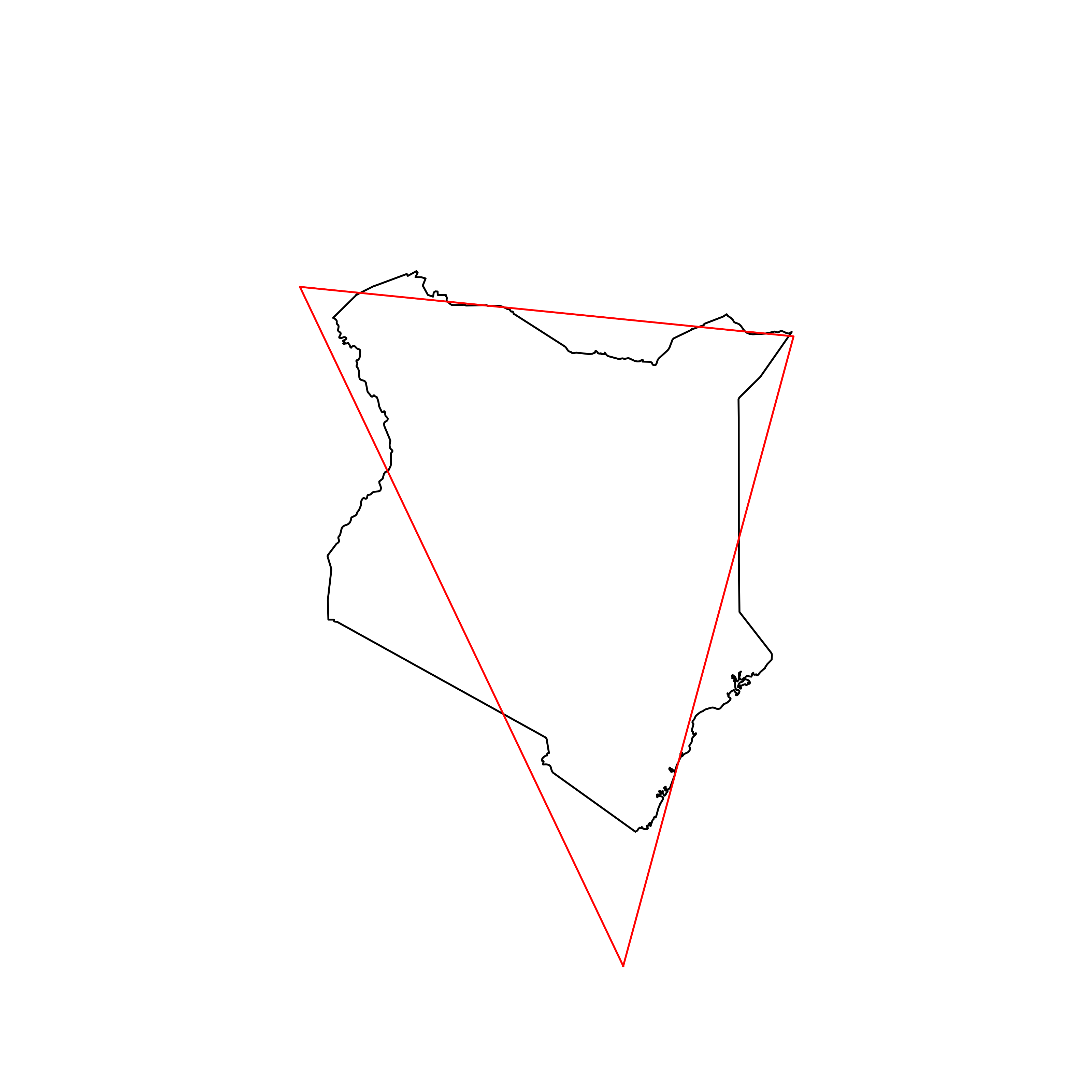 |
| 83 | Australia | 0.844598 | 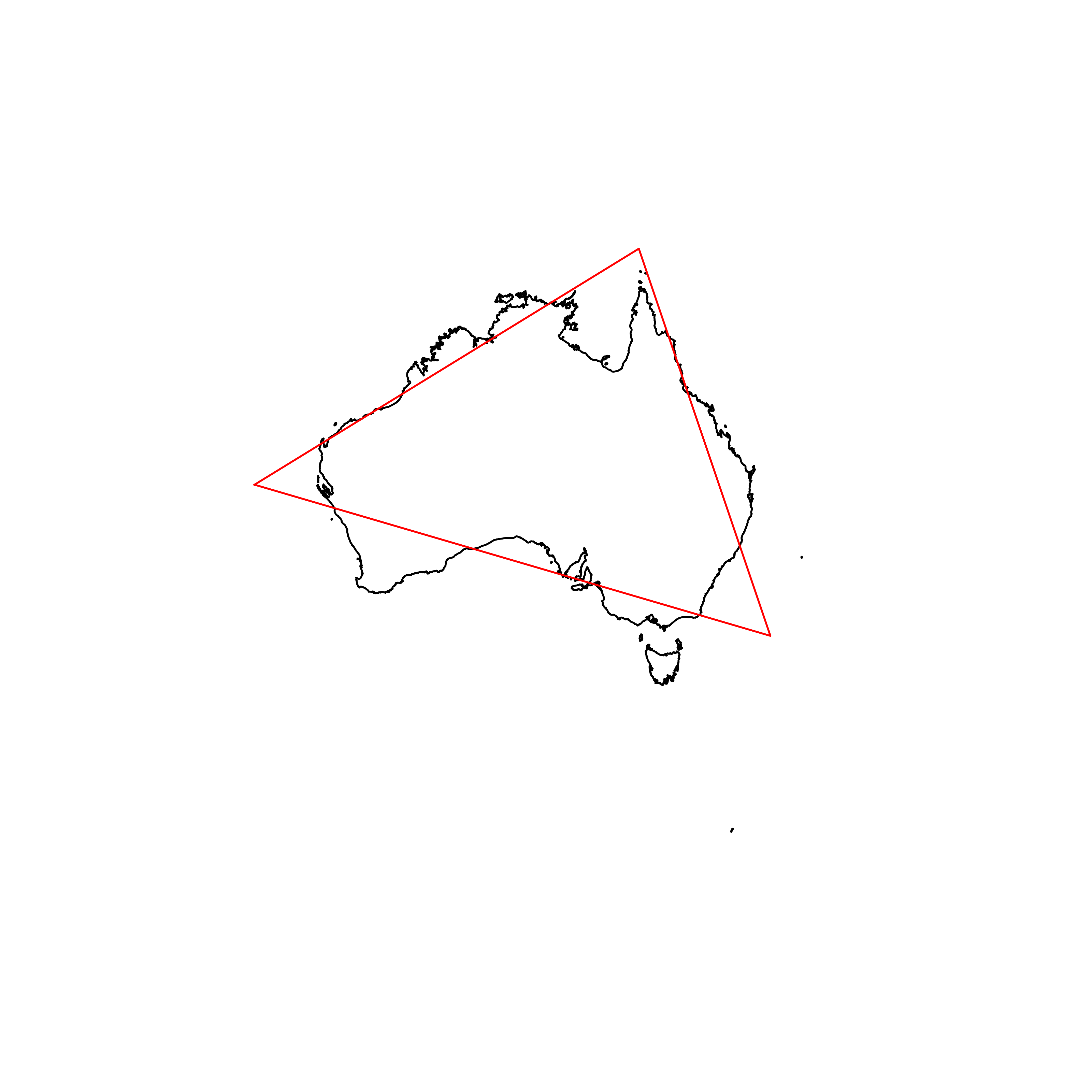 |
| 84 | Cyprus | 0.844447 | 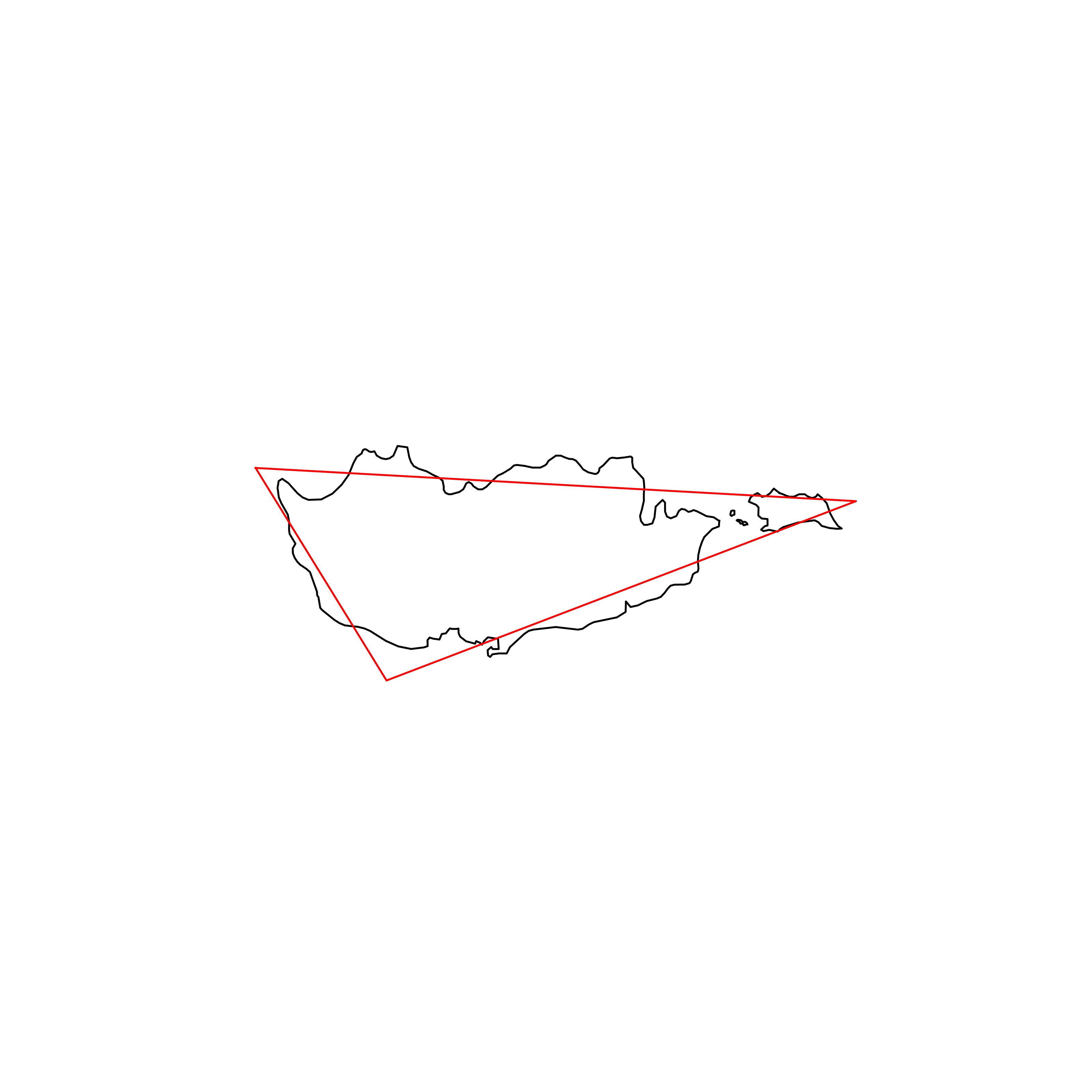 |
| 85 | United Arab Emirates | 0.844364 | 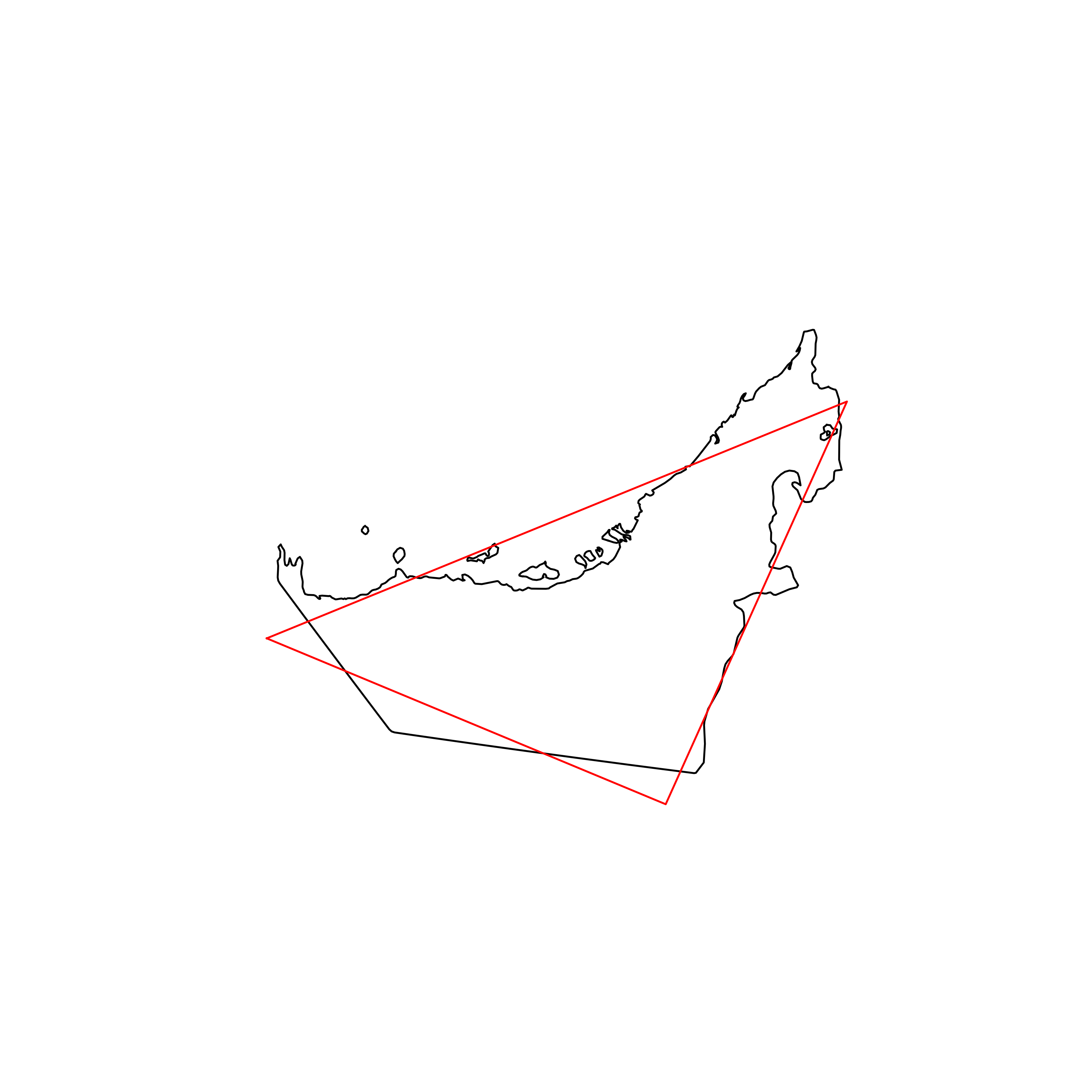 |
| 86 | Montenegro | 0.842538 | 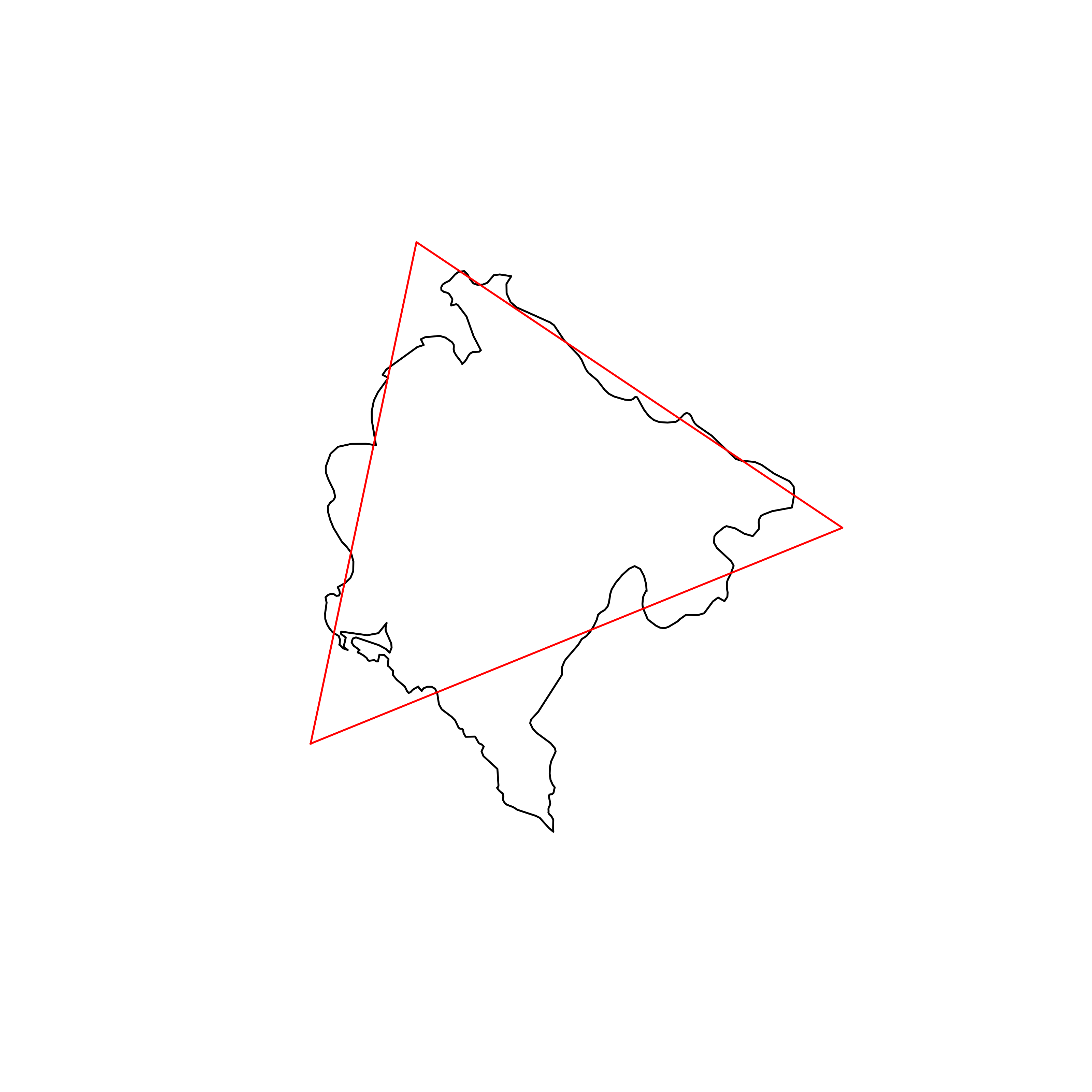 |
| 87 | Macedonia | 0.842095 | 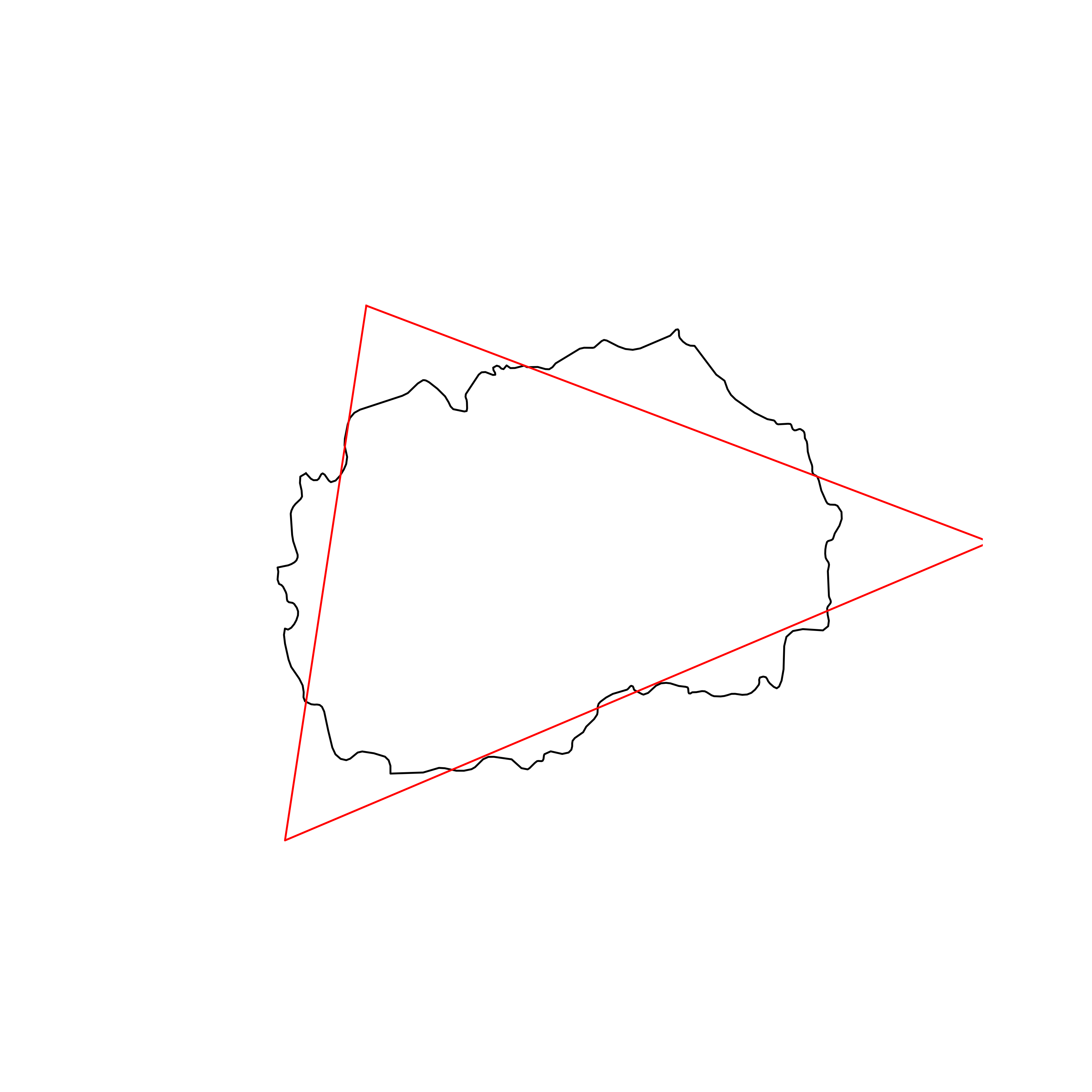 |
| 88 | Ireland | 0.841491 | 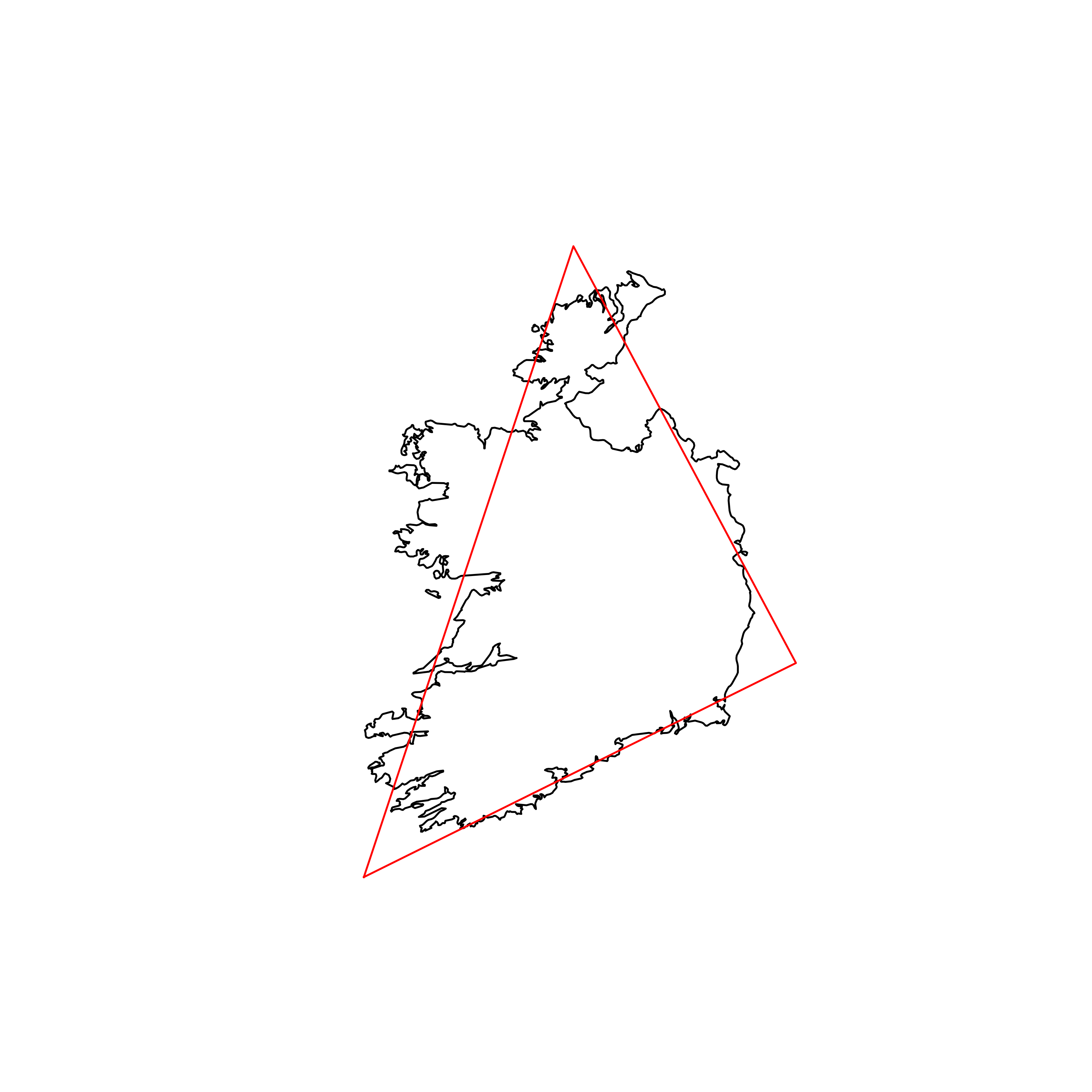 |
| 89 | Jamaica | 0.840451 |  |
| 90 | Senegal | 0.840054 | 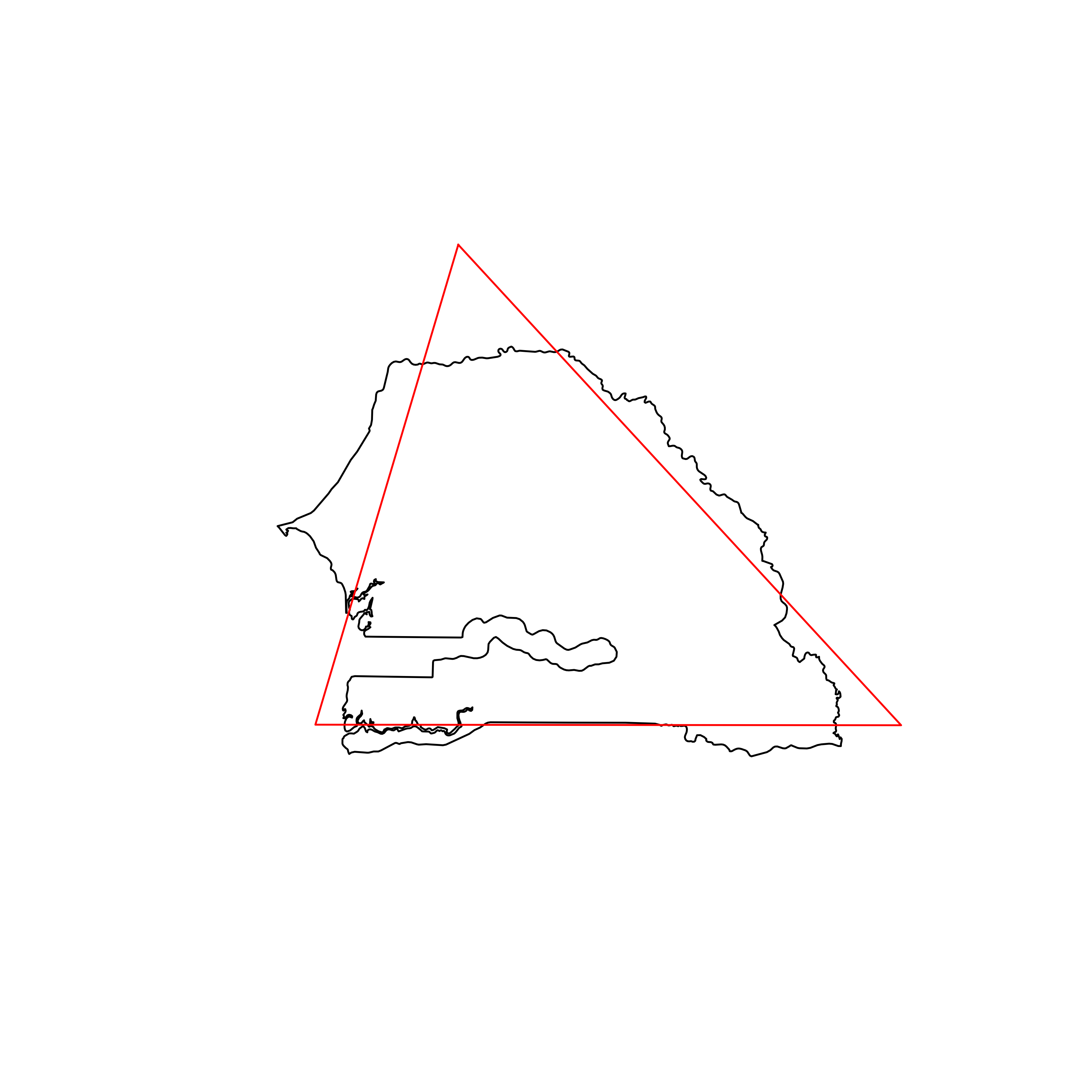 |
| 91 | Suriname | 0.839448 | 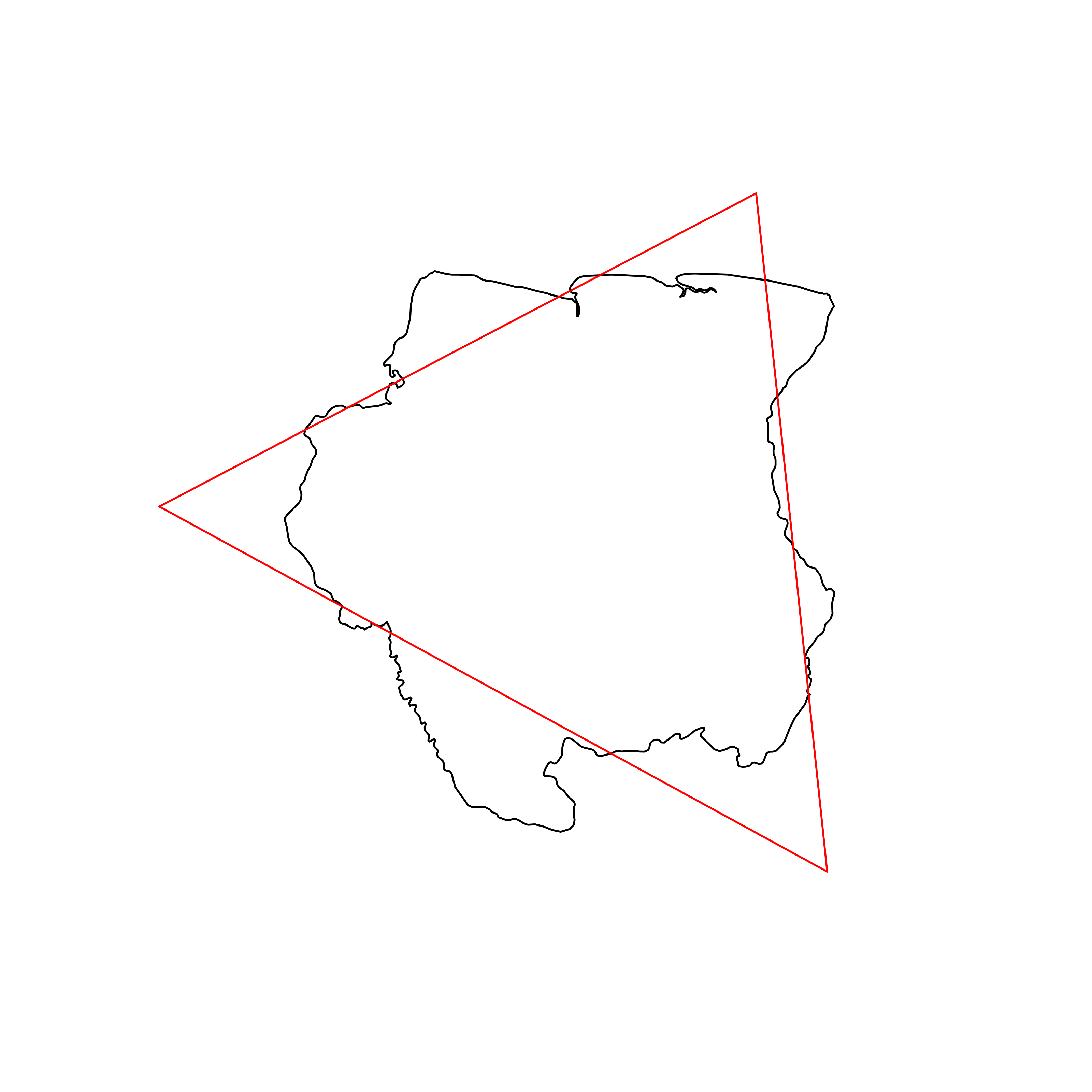 |
| 92 | Turkey | 0.838539 | 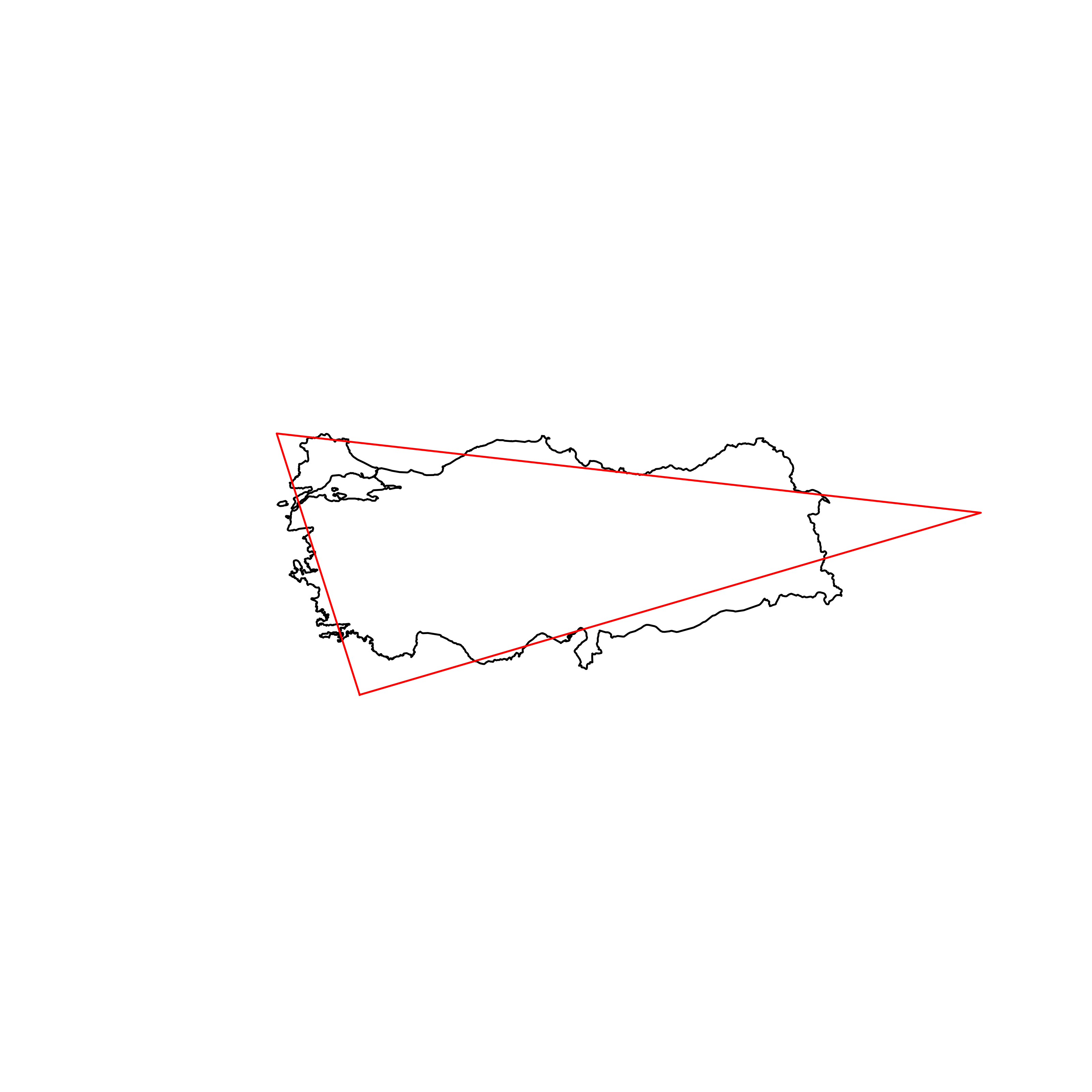 |
| 93 | Pakistan | 0.838210 | 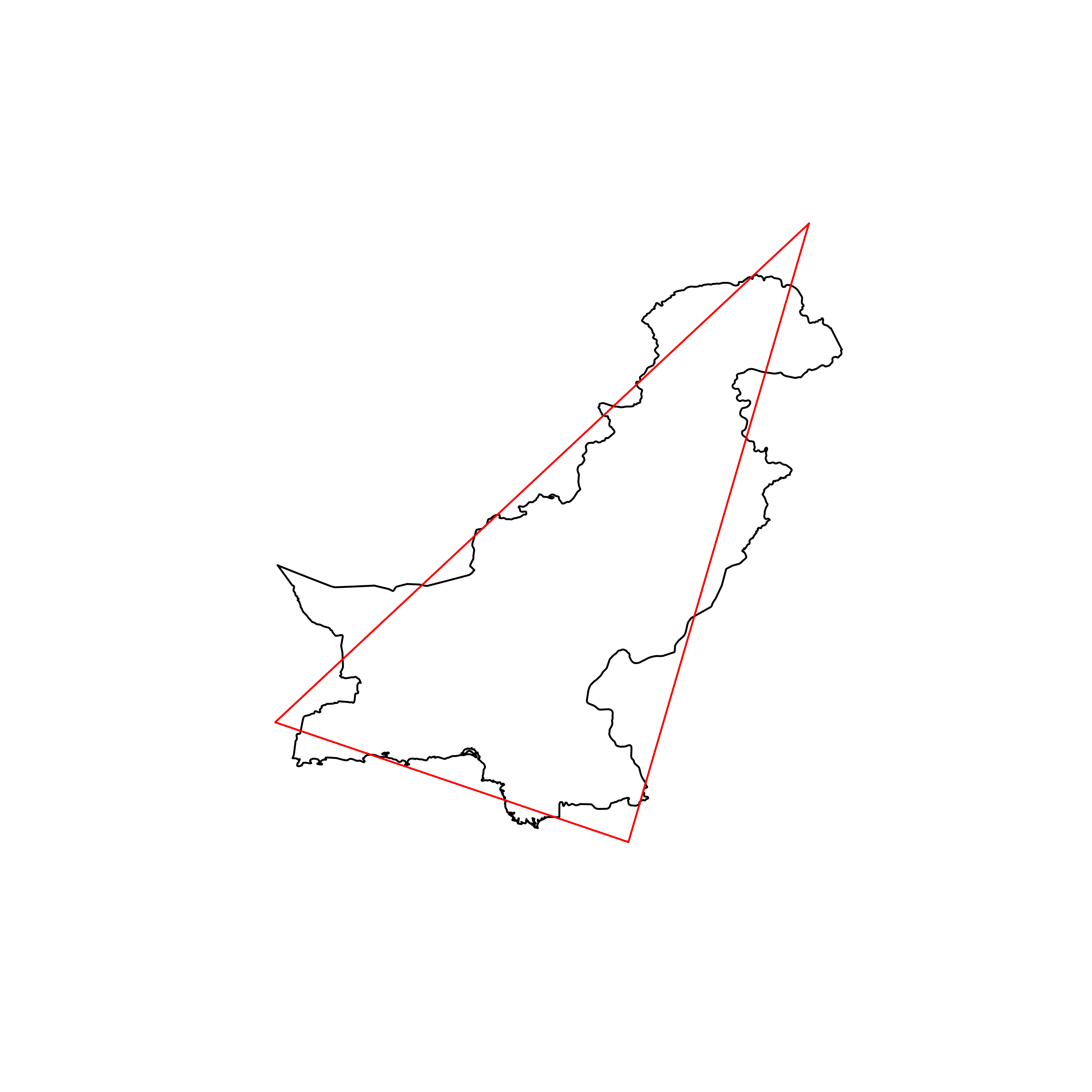 |
| 94 | Nauru | 0.838165 | 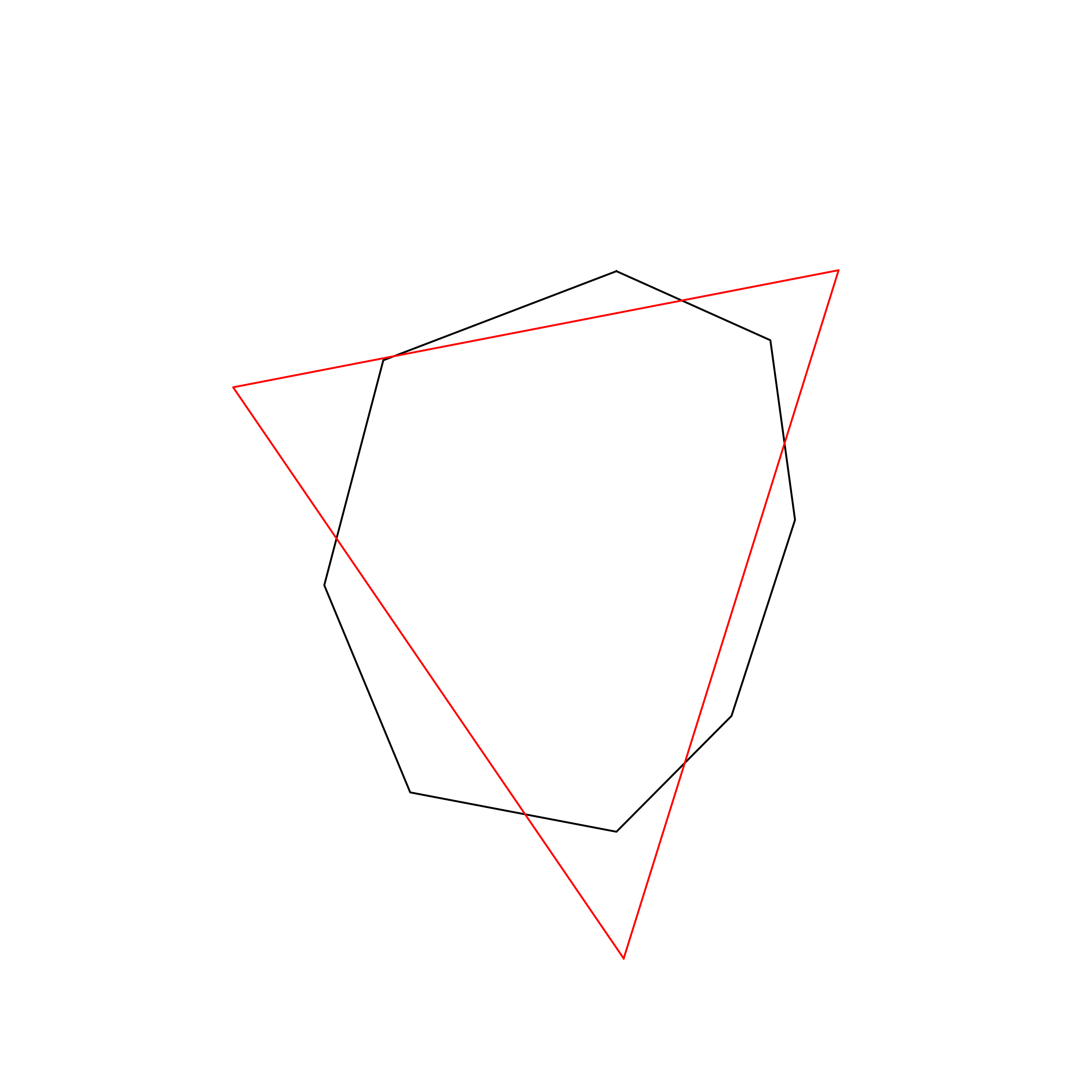 |
| 95 | Iceland | 0.837977 | 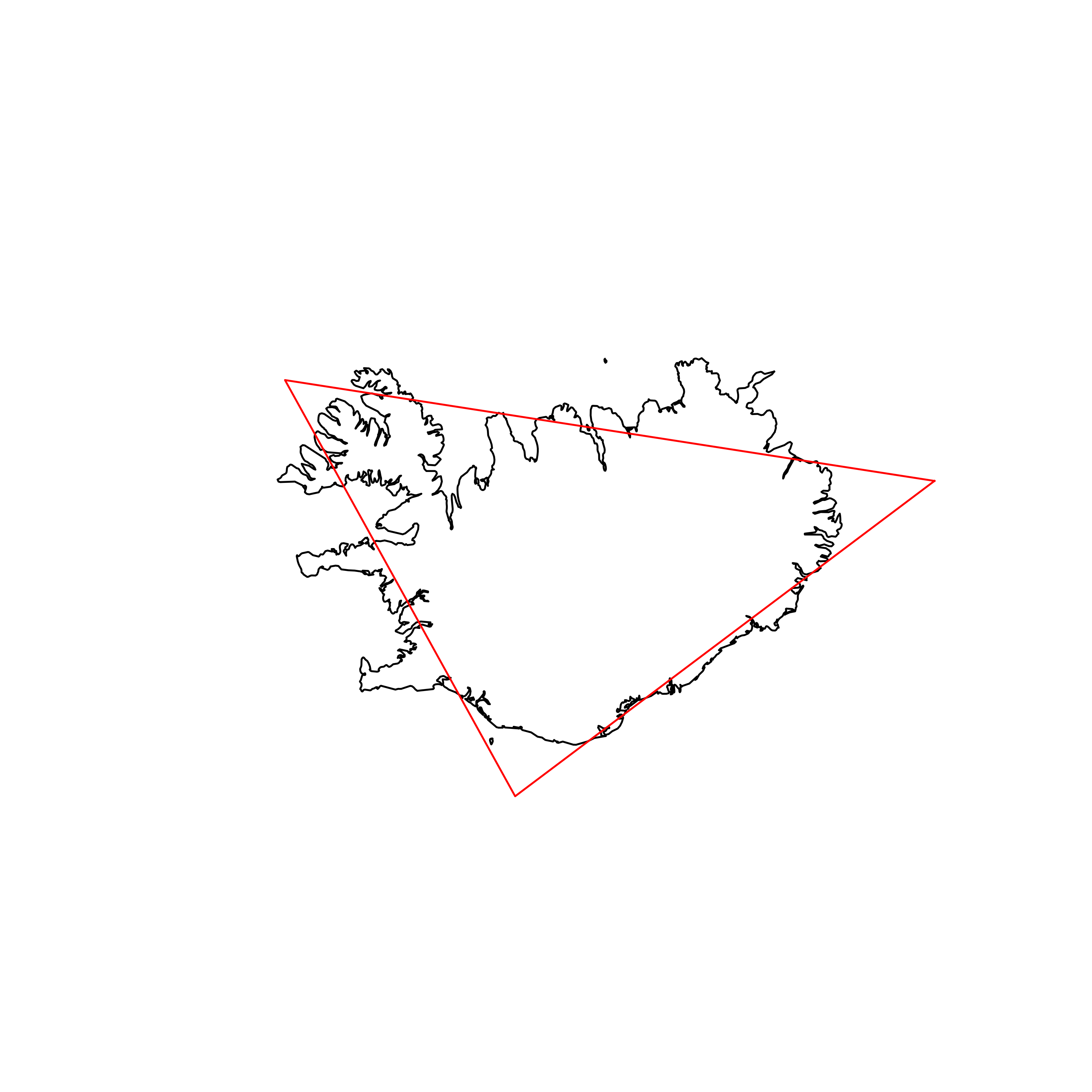 |
| 96 | Qatar | 0.837840 | 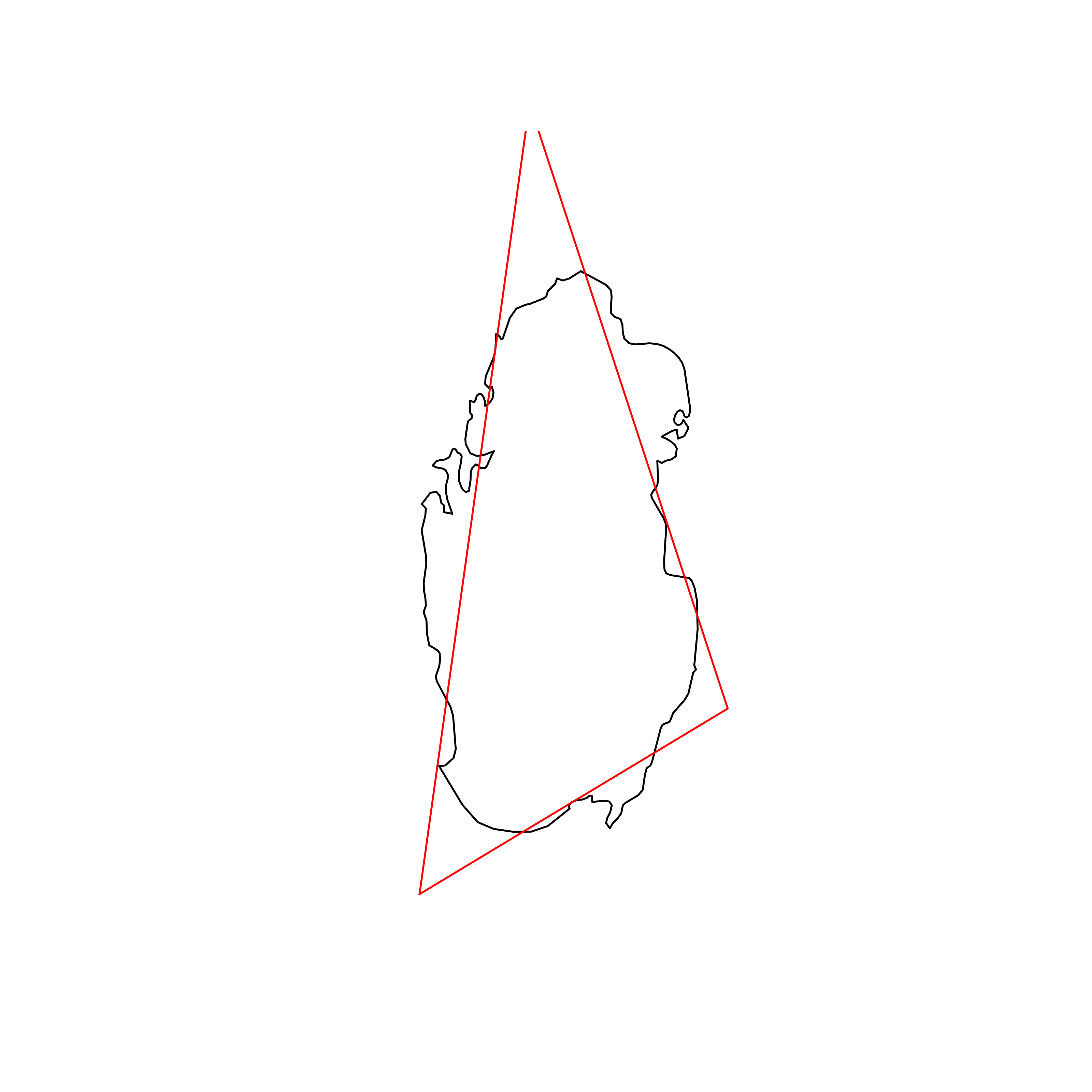 |
| 97 | Mali | 0.837820 | 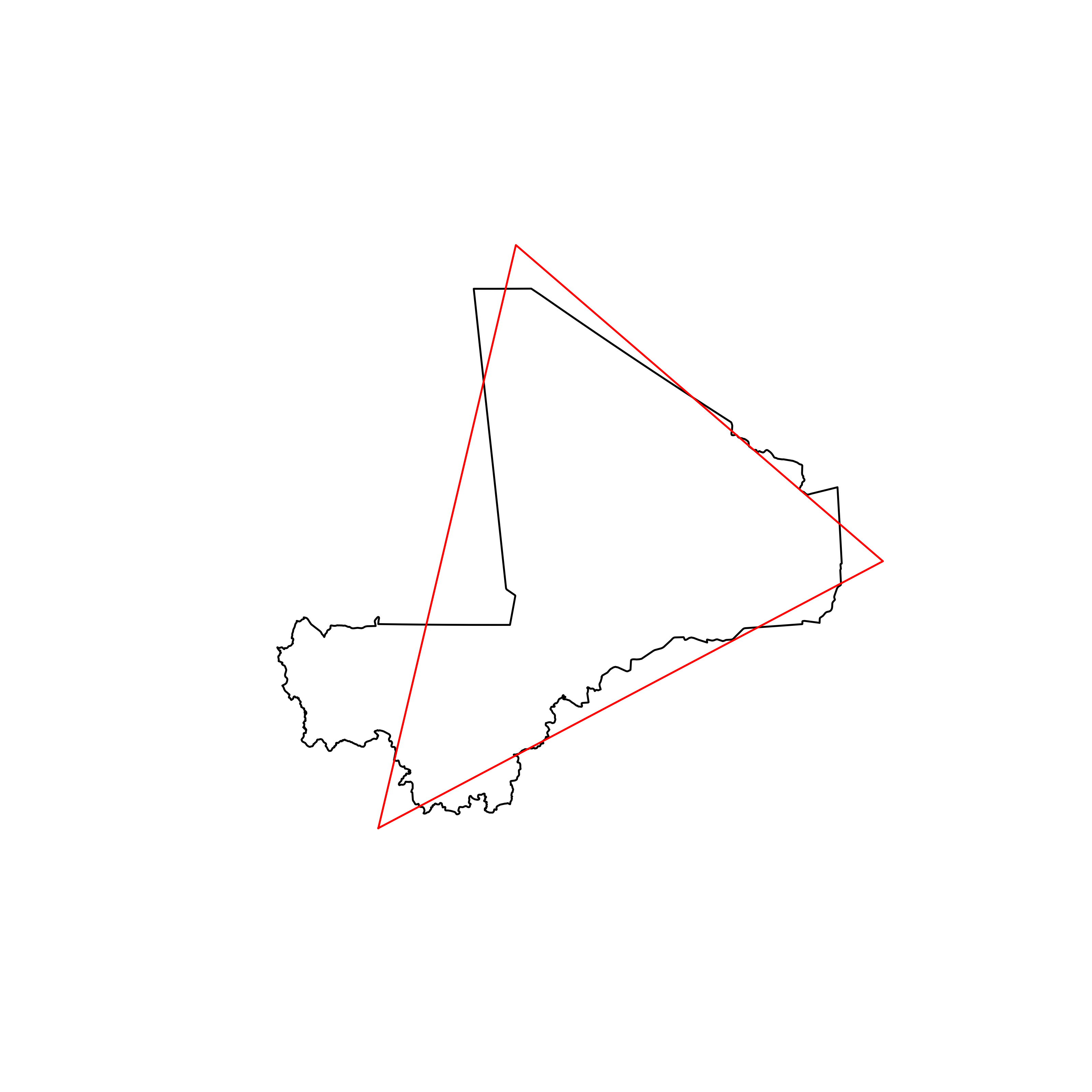 |
| 98 | Sudan | 0.837108 | 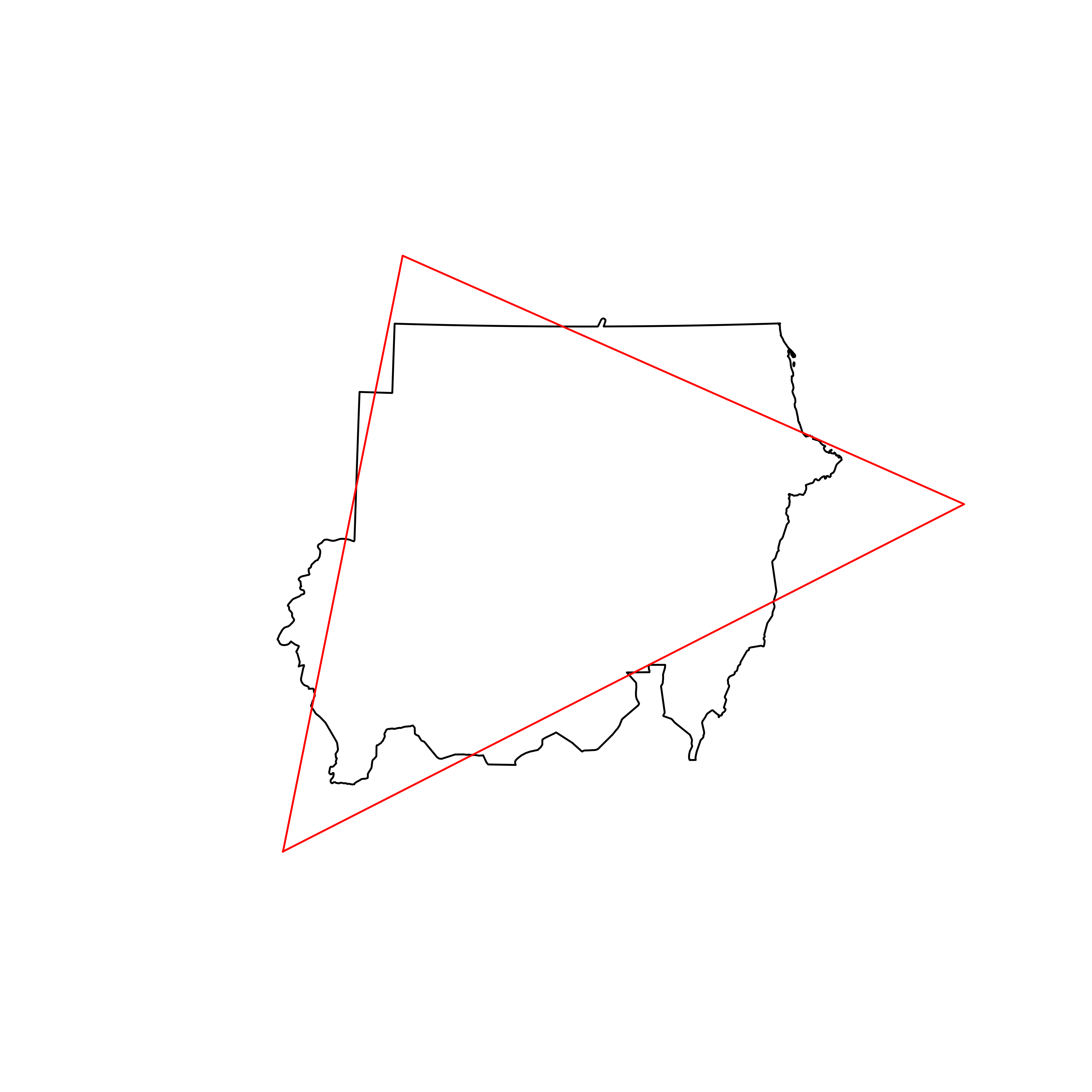 |
| 99 | Albania | 0.836750 | 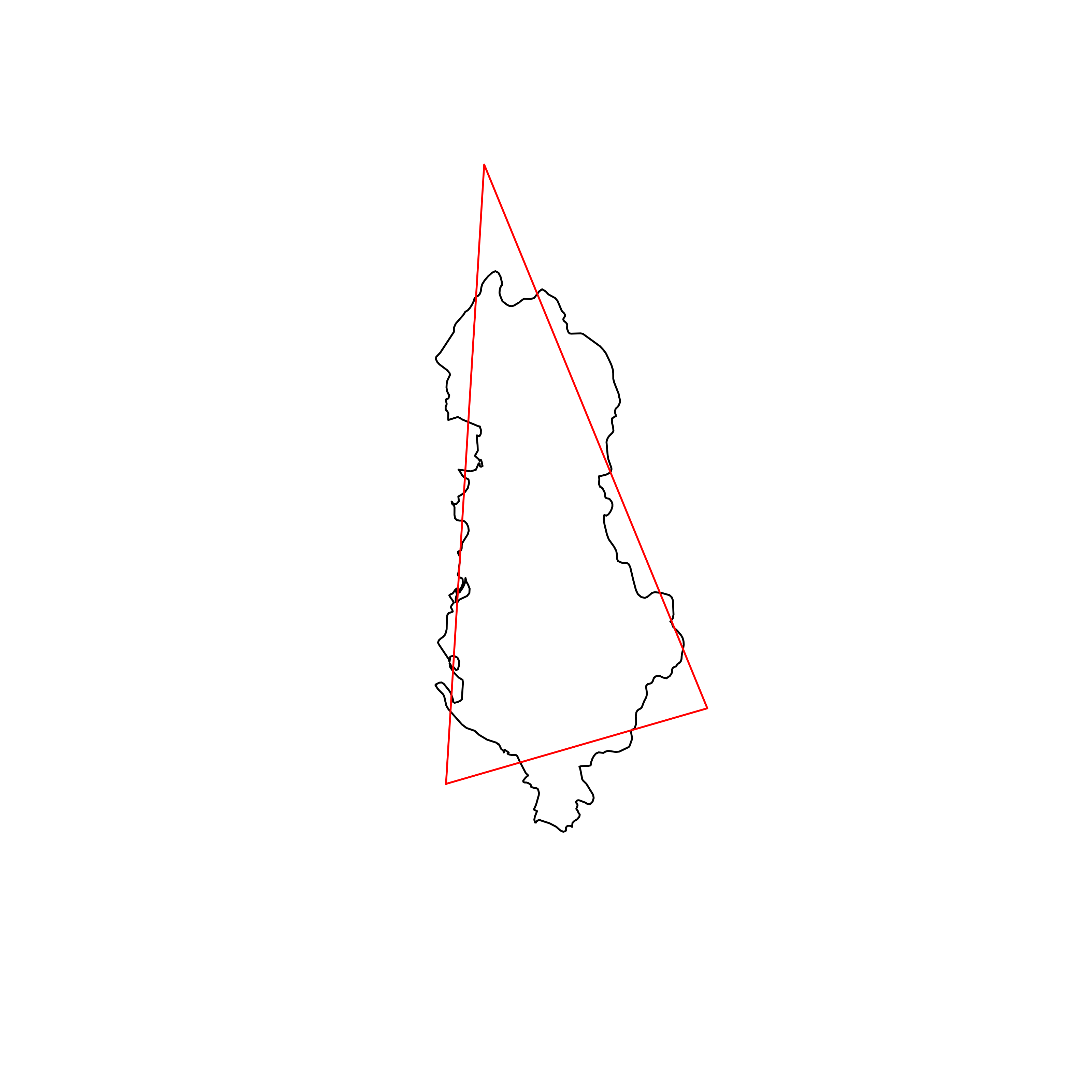 |
| 100 | Czechia | 0.836644 | 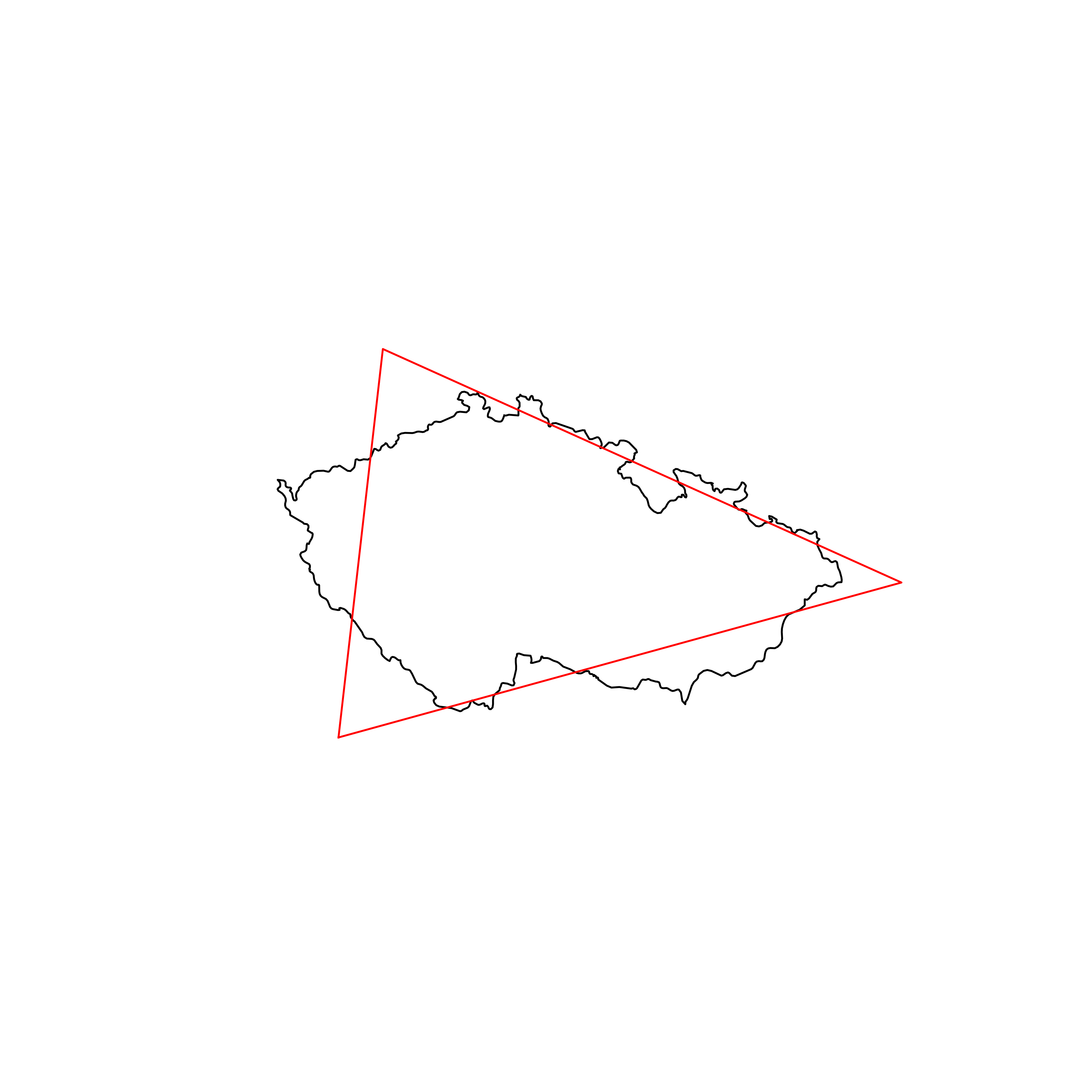 |
| 101 | Togo | 0.836207 | 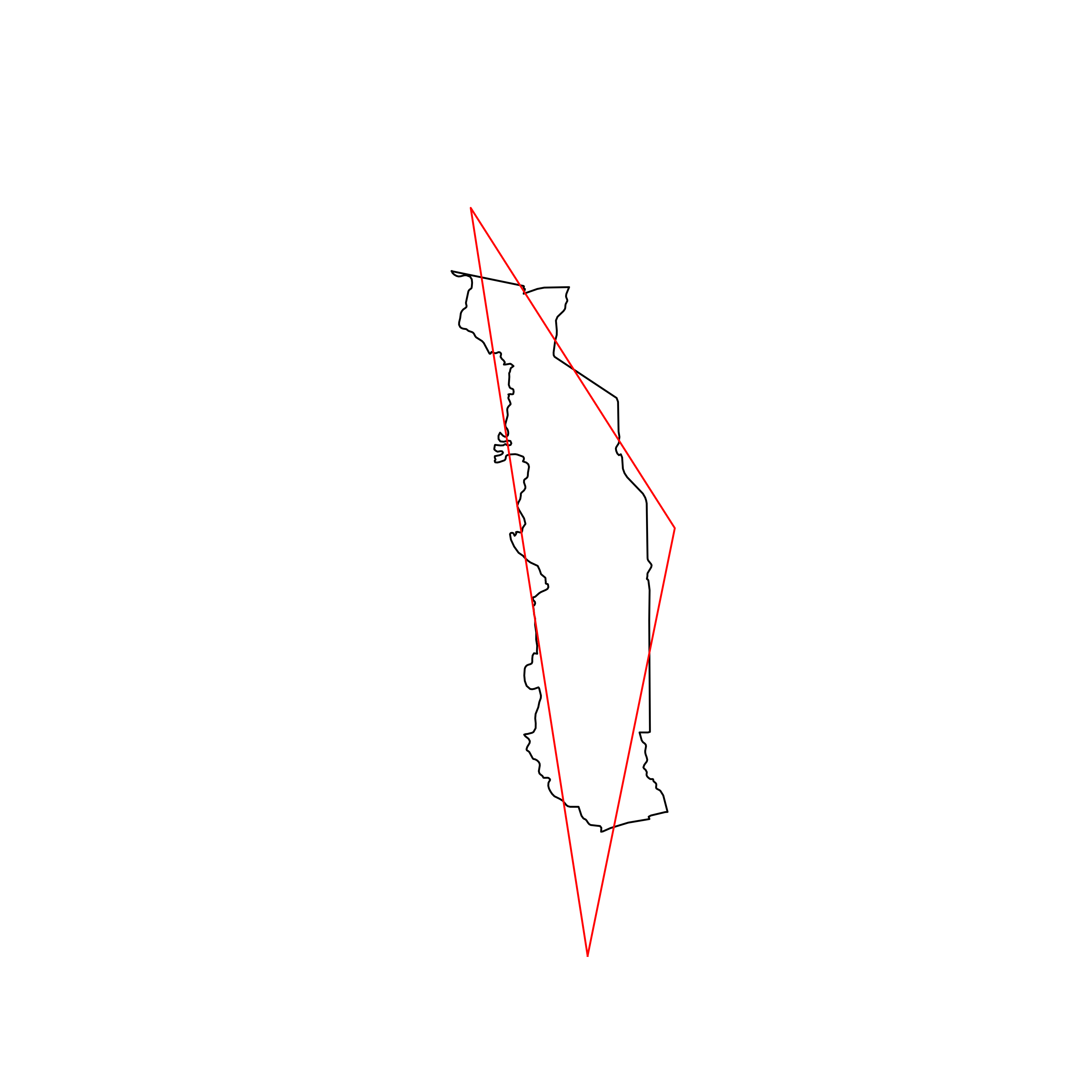 |
| 102 | Iran | 0.835827 | 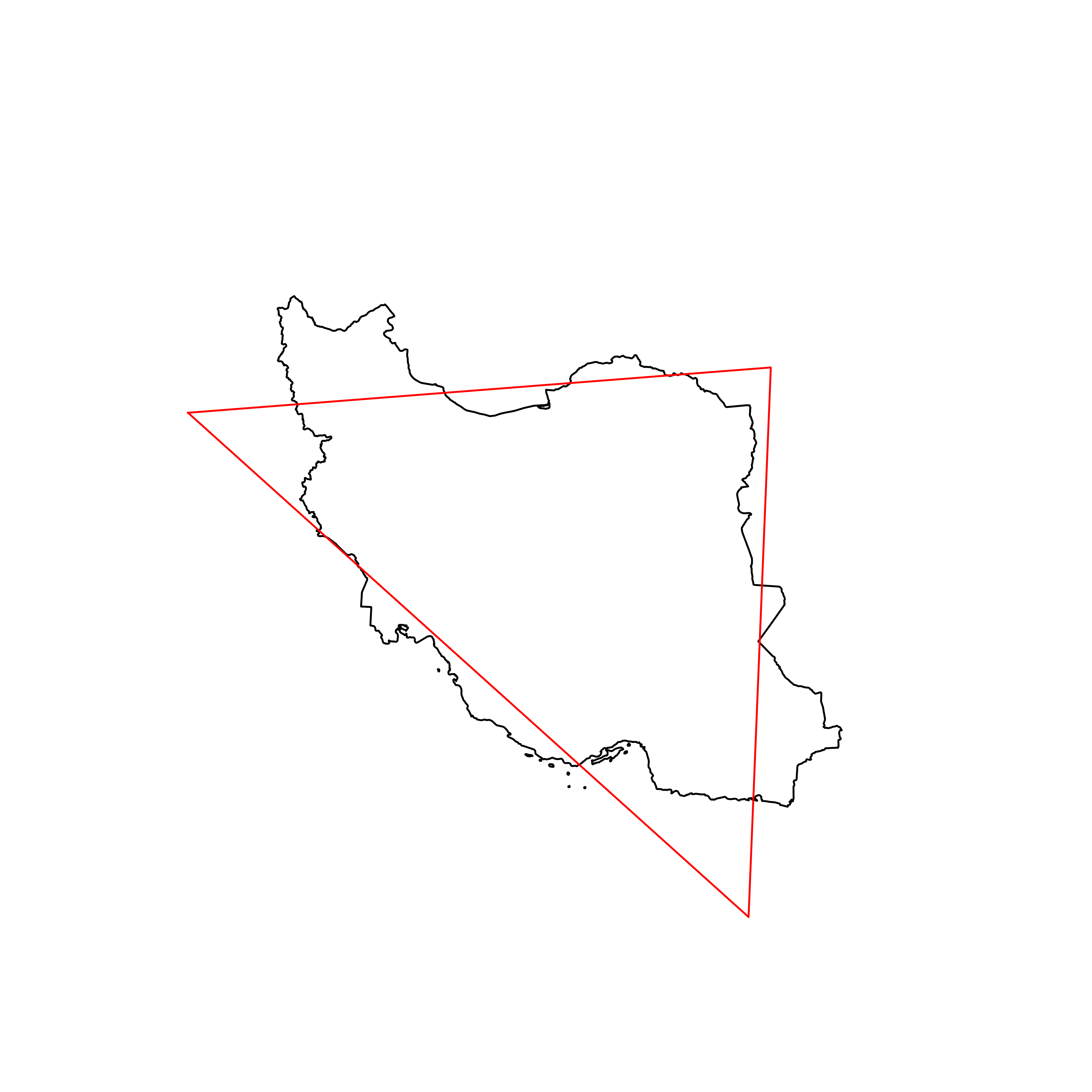 |
| 103 | Sierra Leone | 0.835686 | 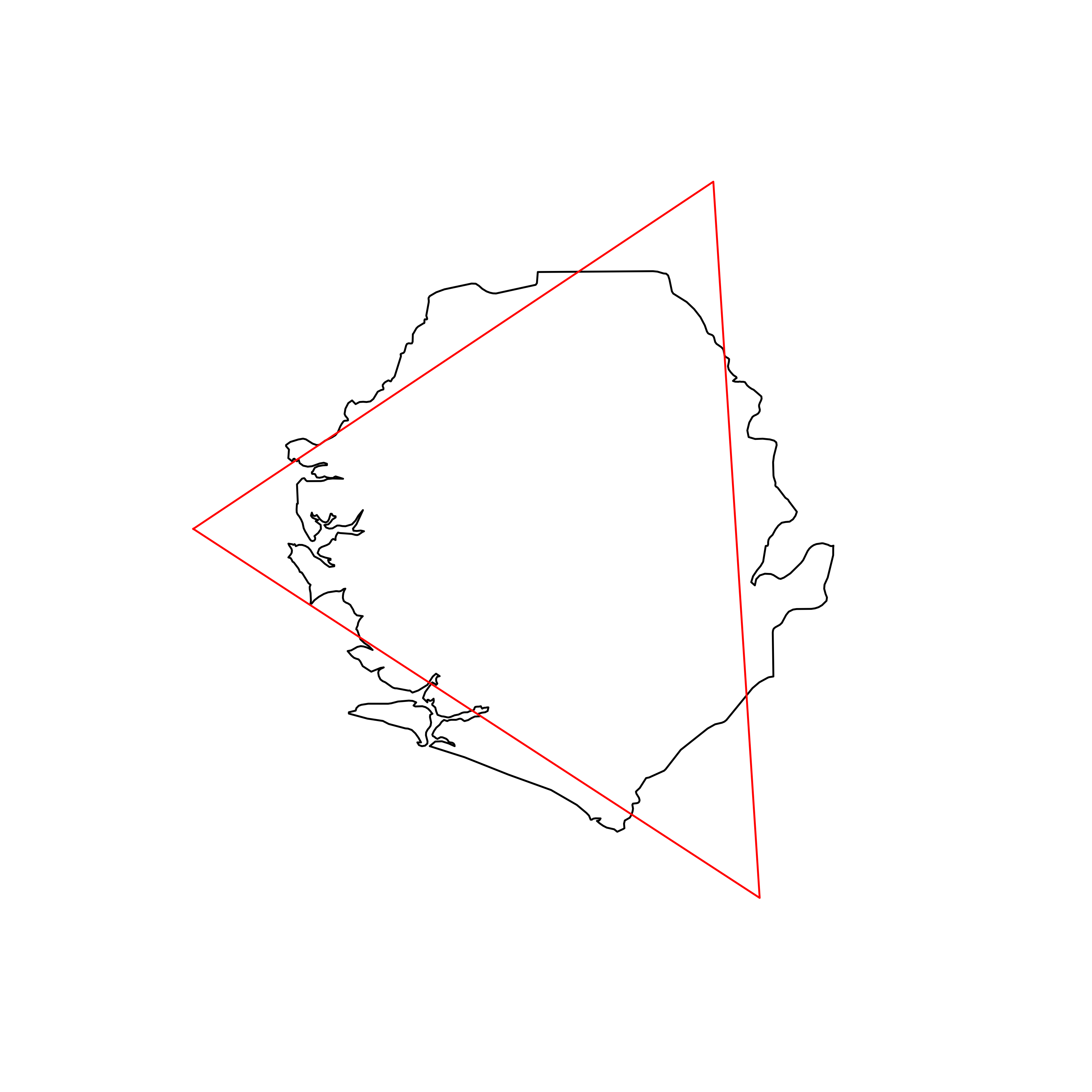 |
| 104 | Kosovo | 0.834849 | 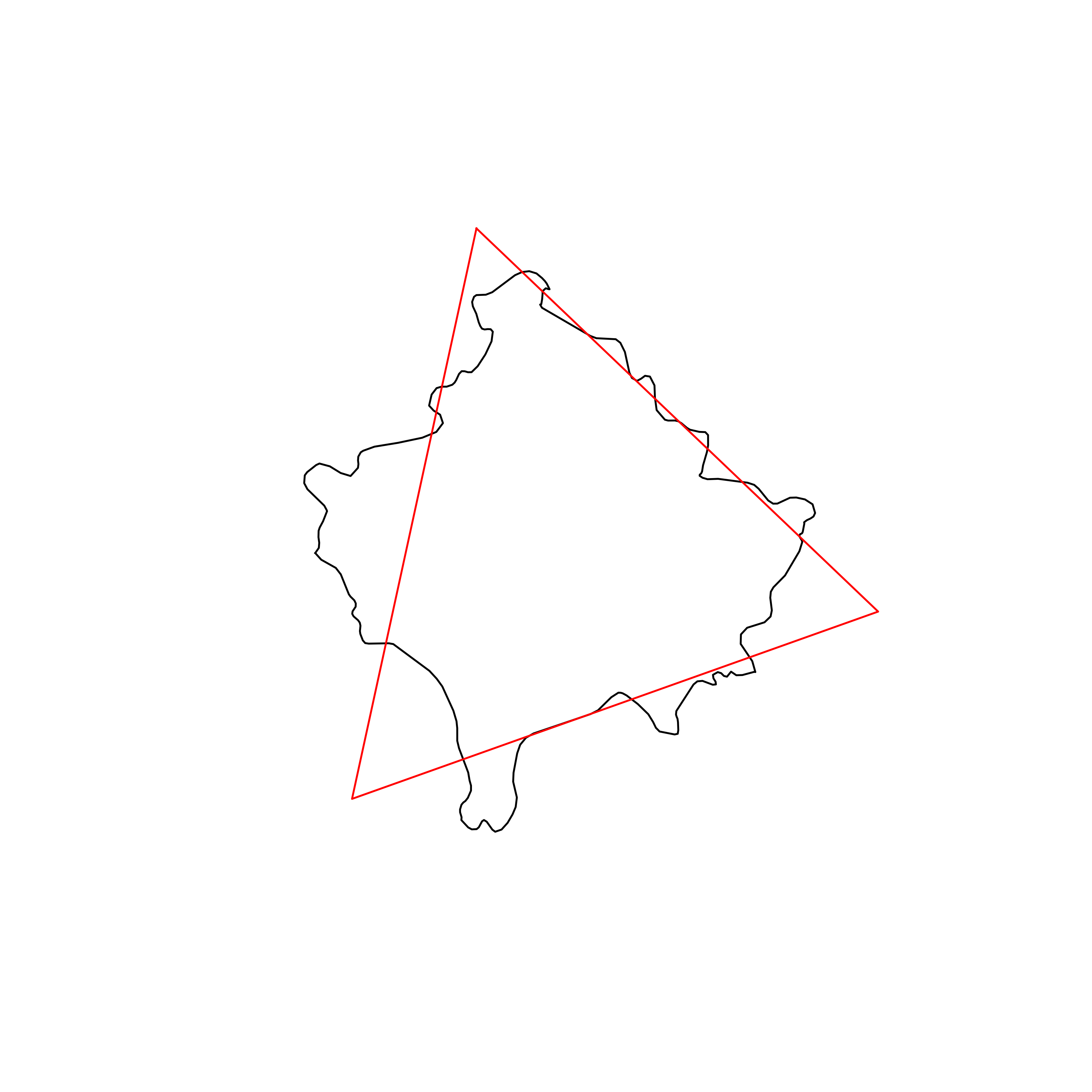 |
| 105 | eSwatini | 0.834460 | 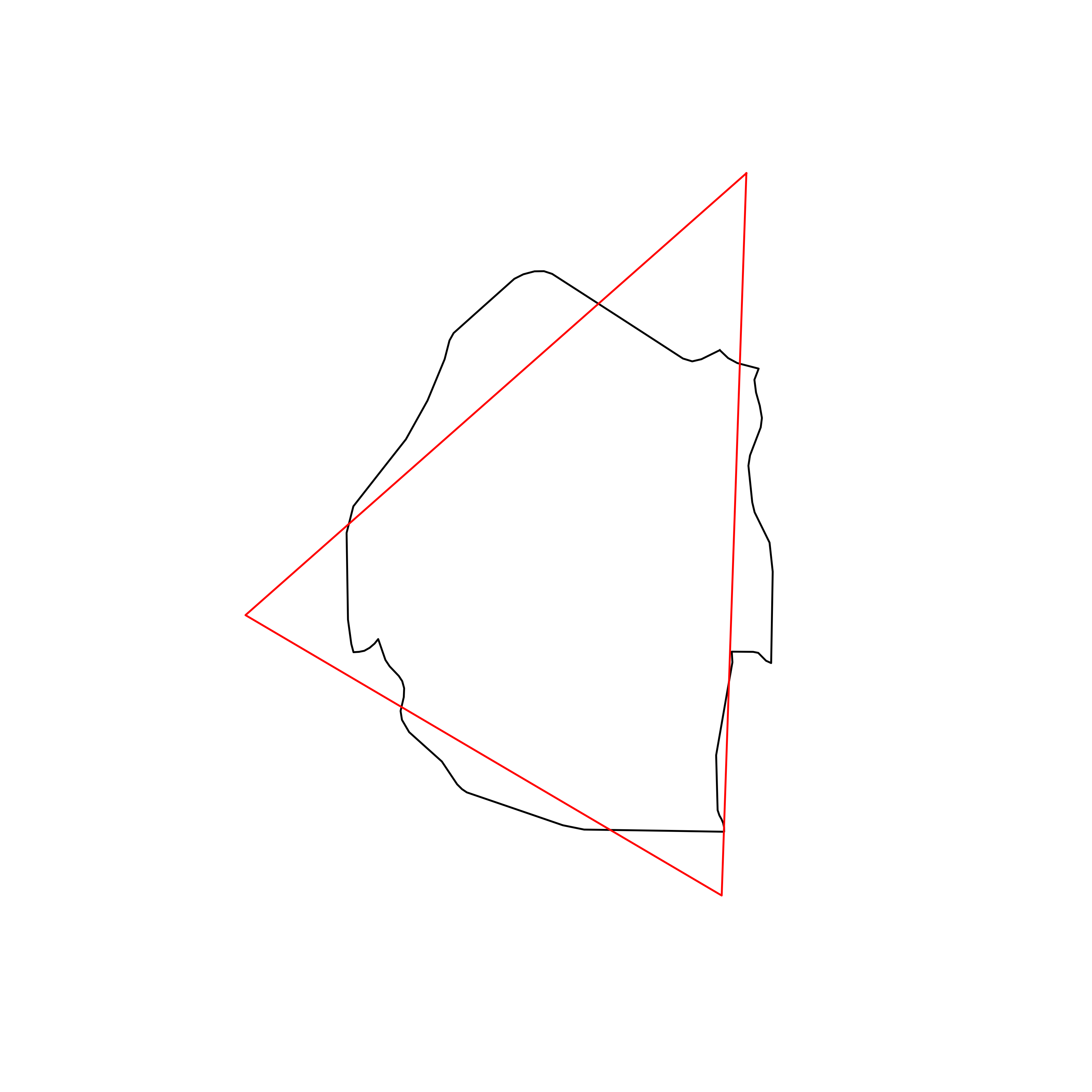 |
| 106 | Gabon | 0.834010 | 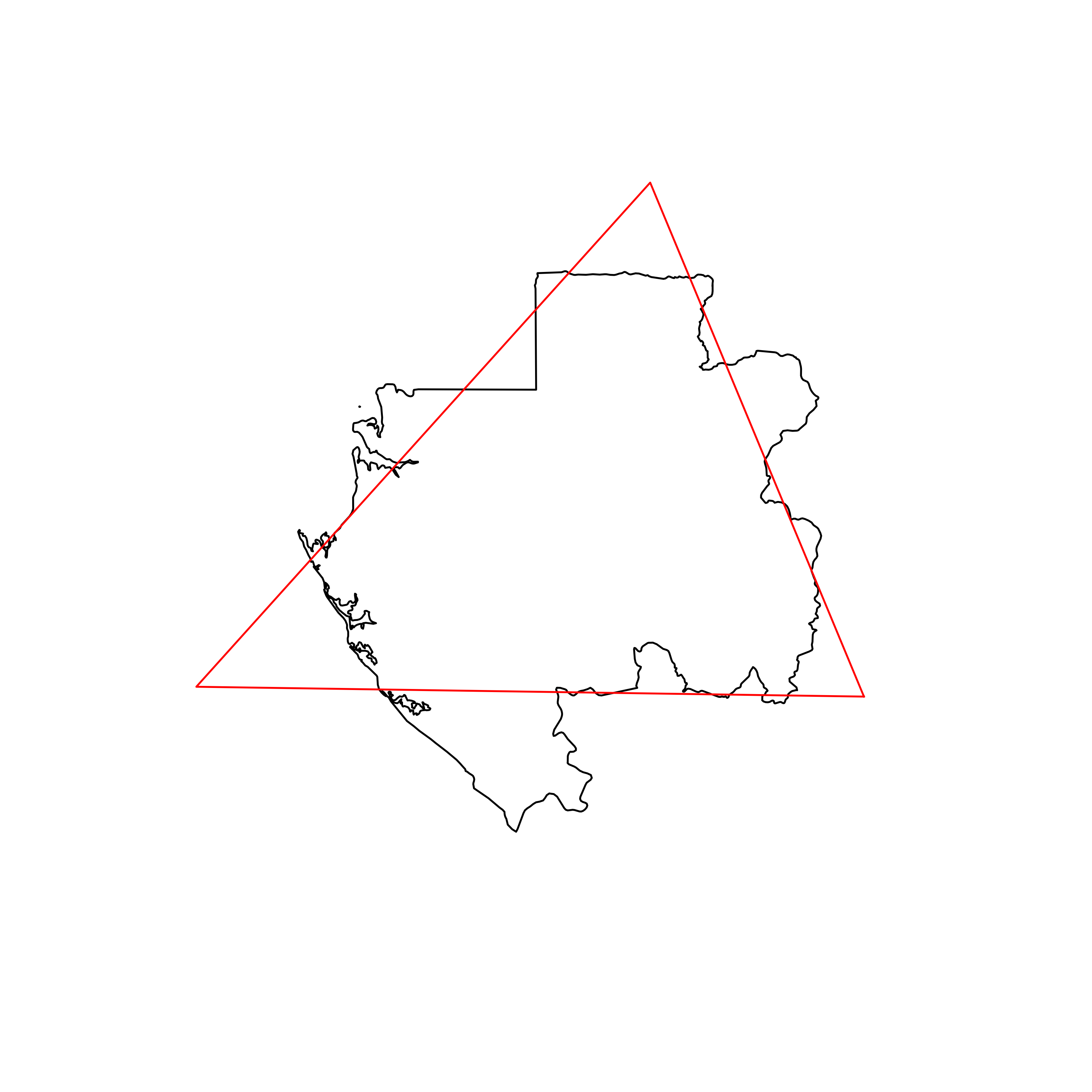 |
| 107 | Bulgaria | 0.833776 | 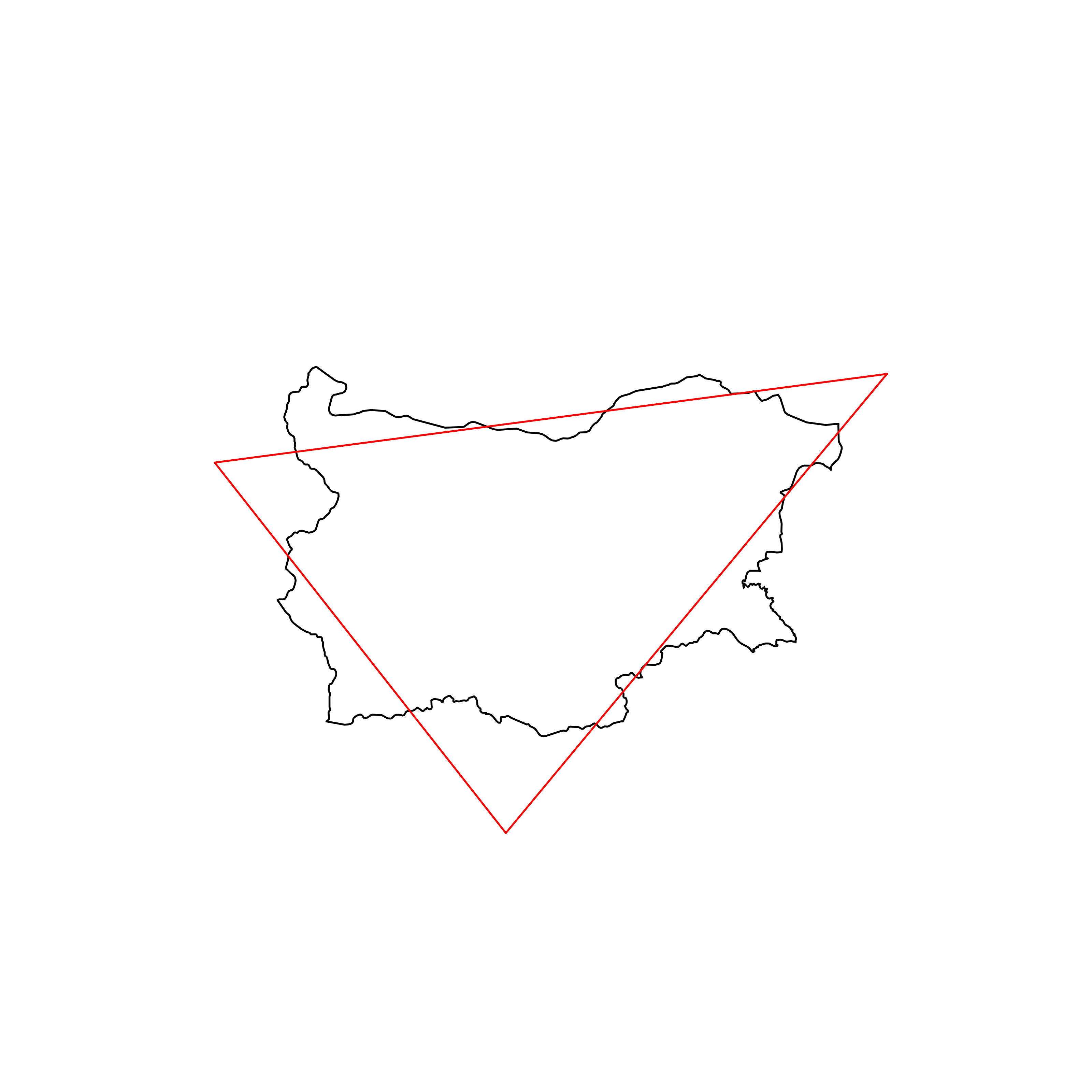 |
| 108 | Angola | 0.832625 | 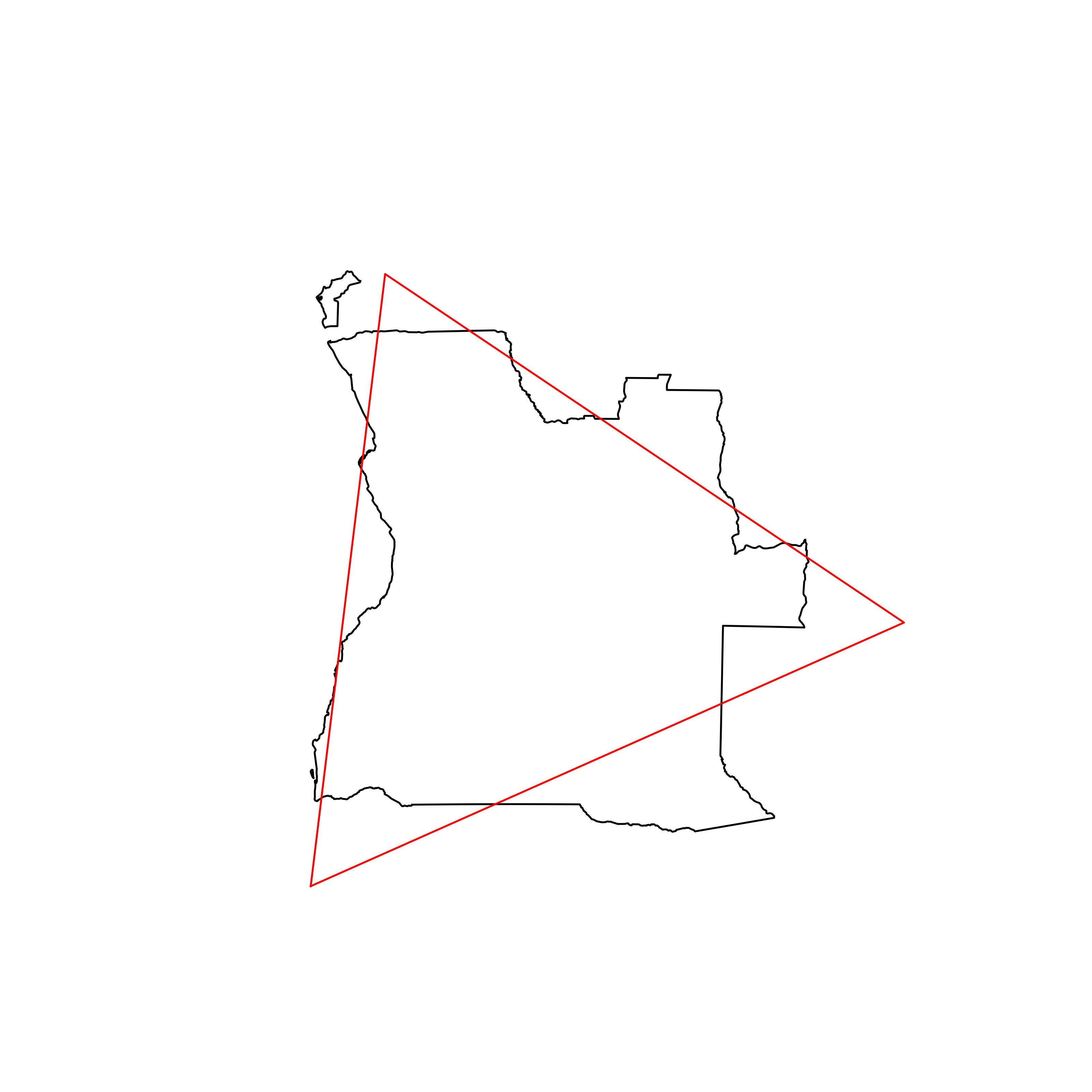 |
| 109 | Oman | 0.832474 | 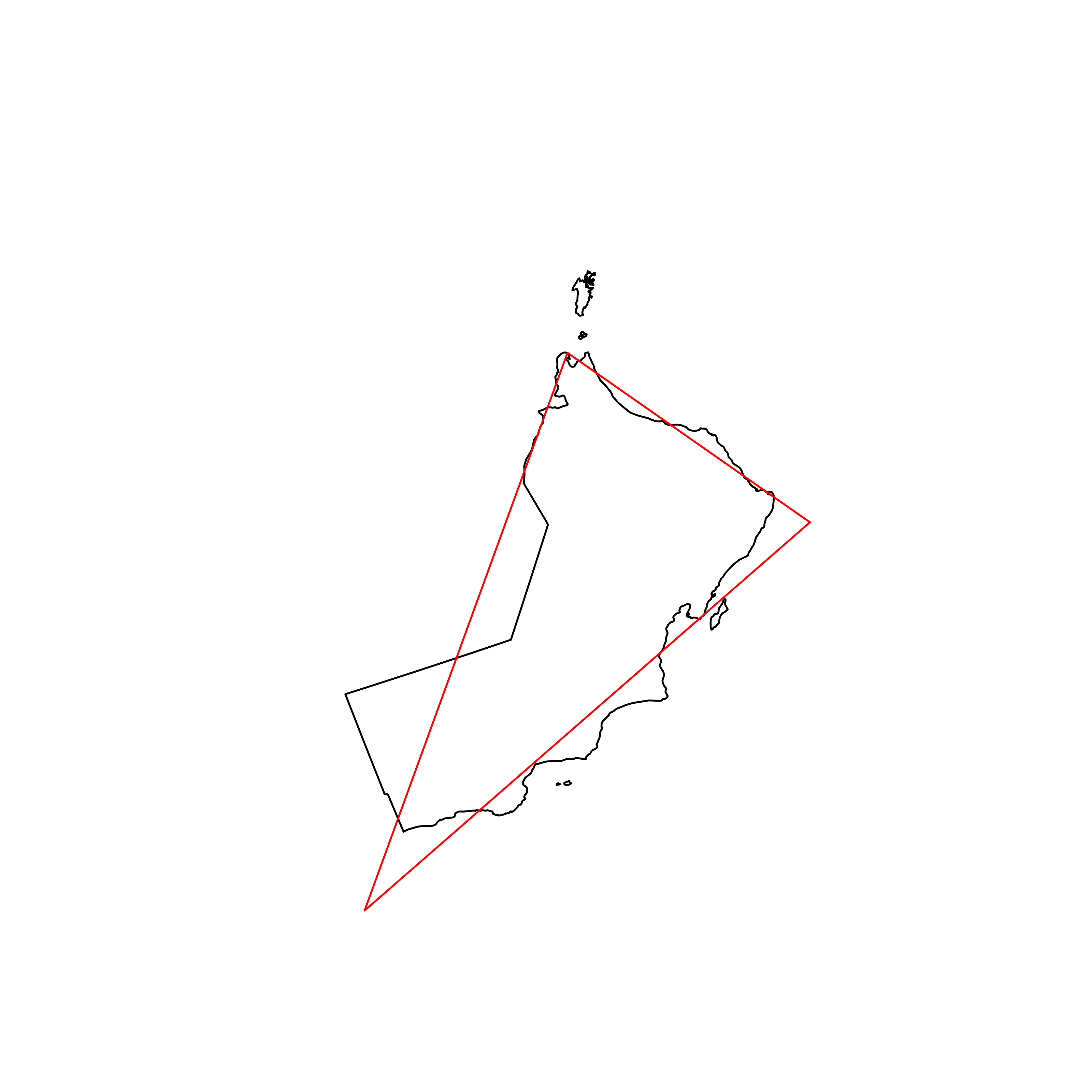 |
| 110 | Lesotho | 0.832316 | 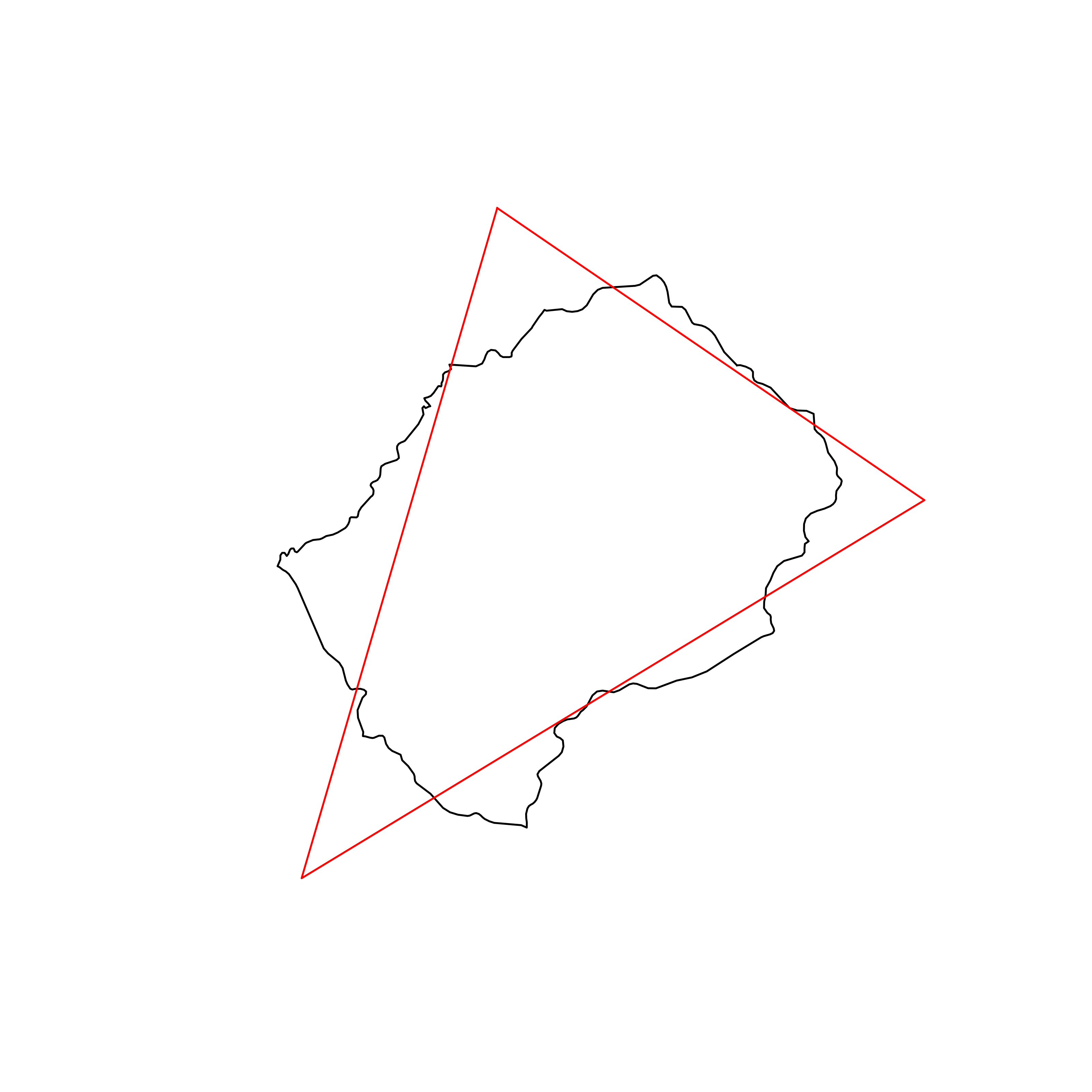 |
| 111 | Germany | 0.832018 | 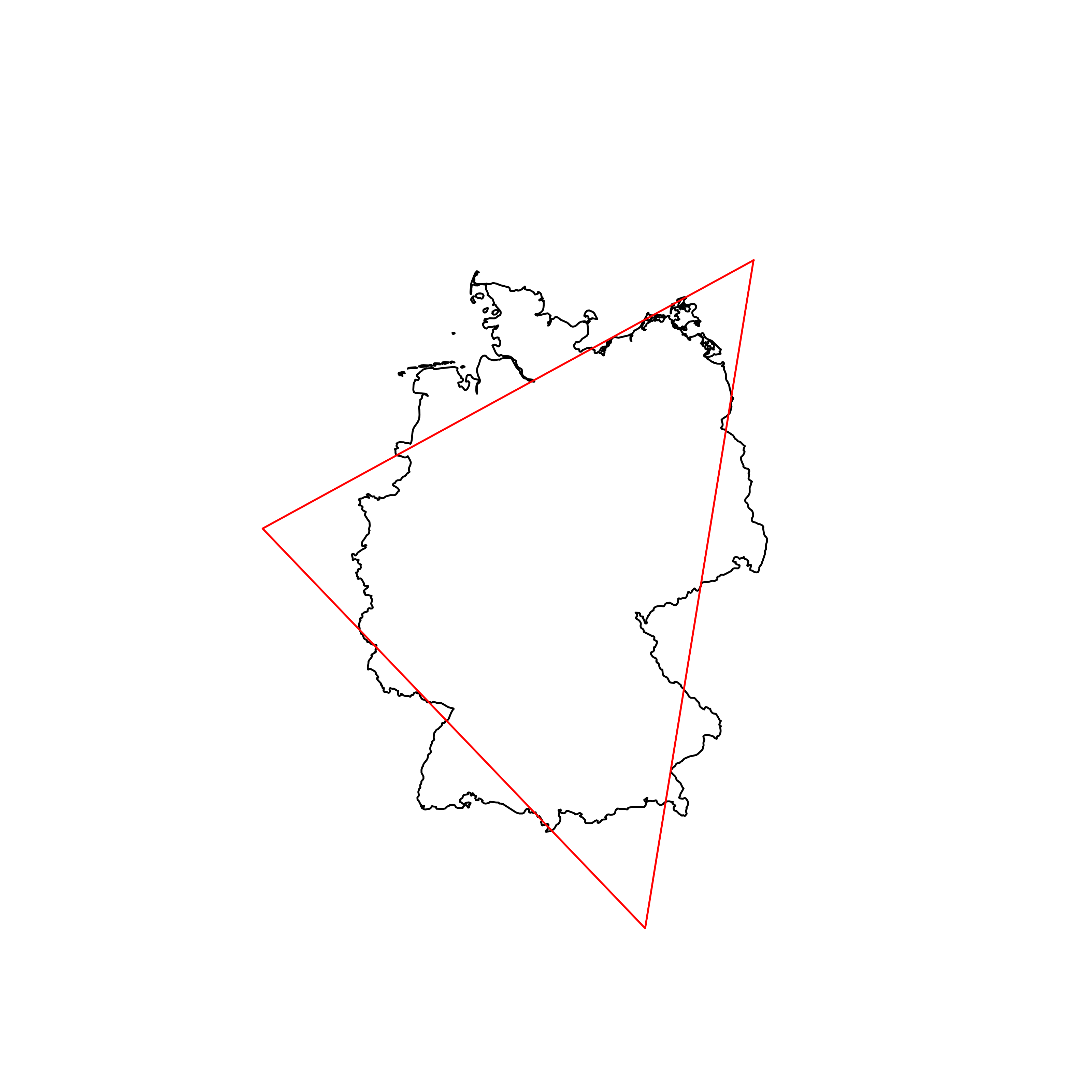 |
| 112 | Rwanda | 0.831329 | 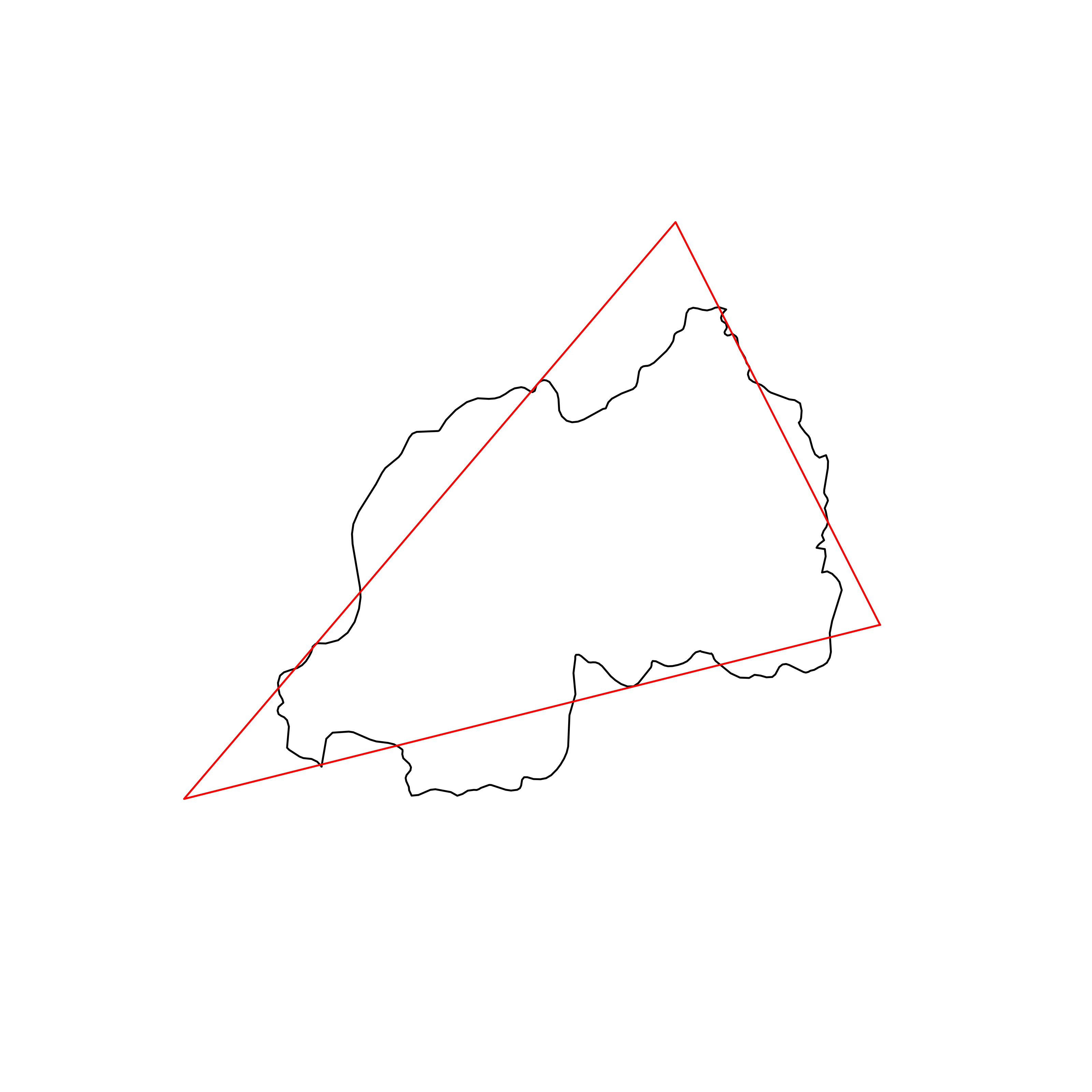 |
| 113 | Switzerland | 0.830879 | 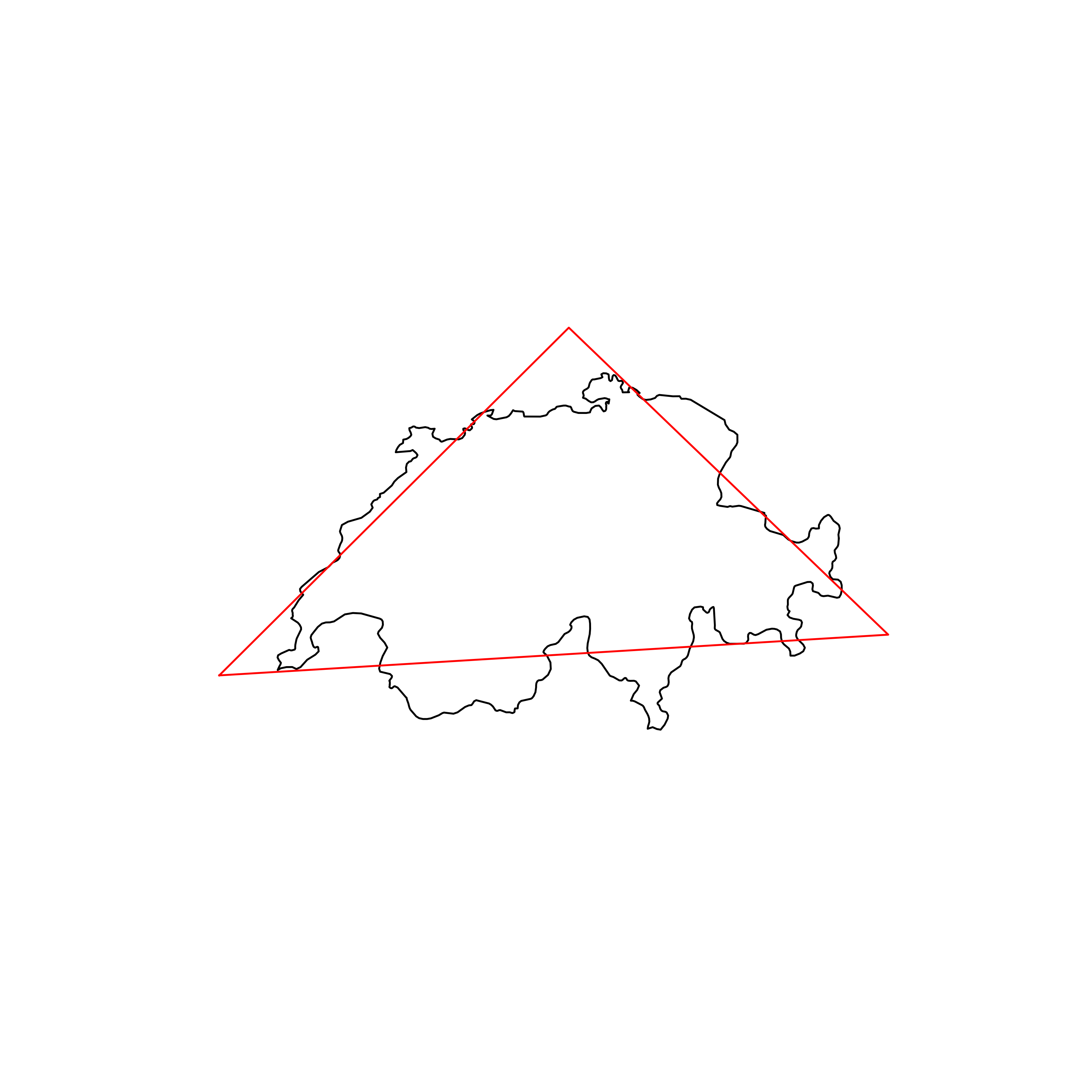 |
| 114 | Belize | 0.830612 | 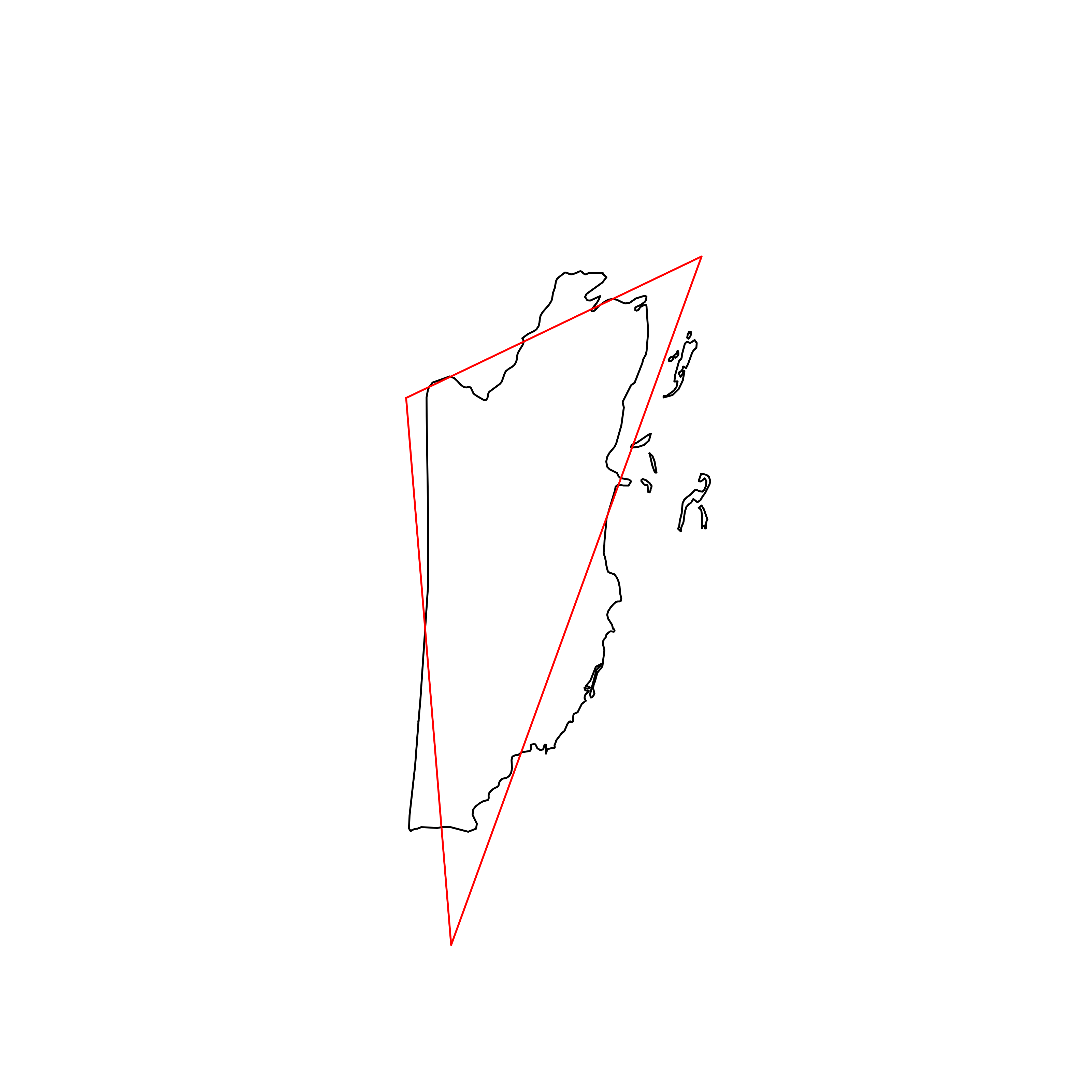 |
| 115 | Guatemala | 0.830442 | 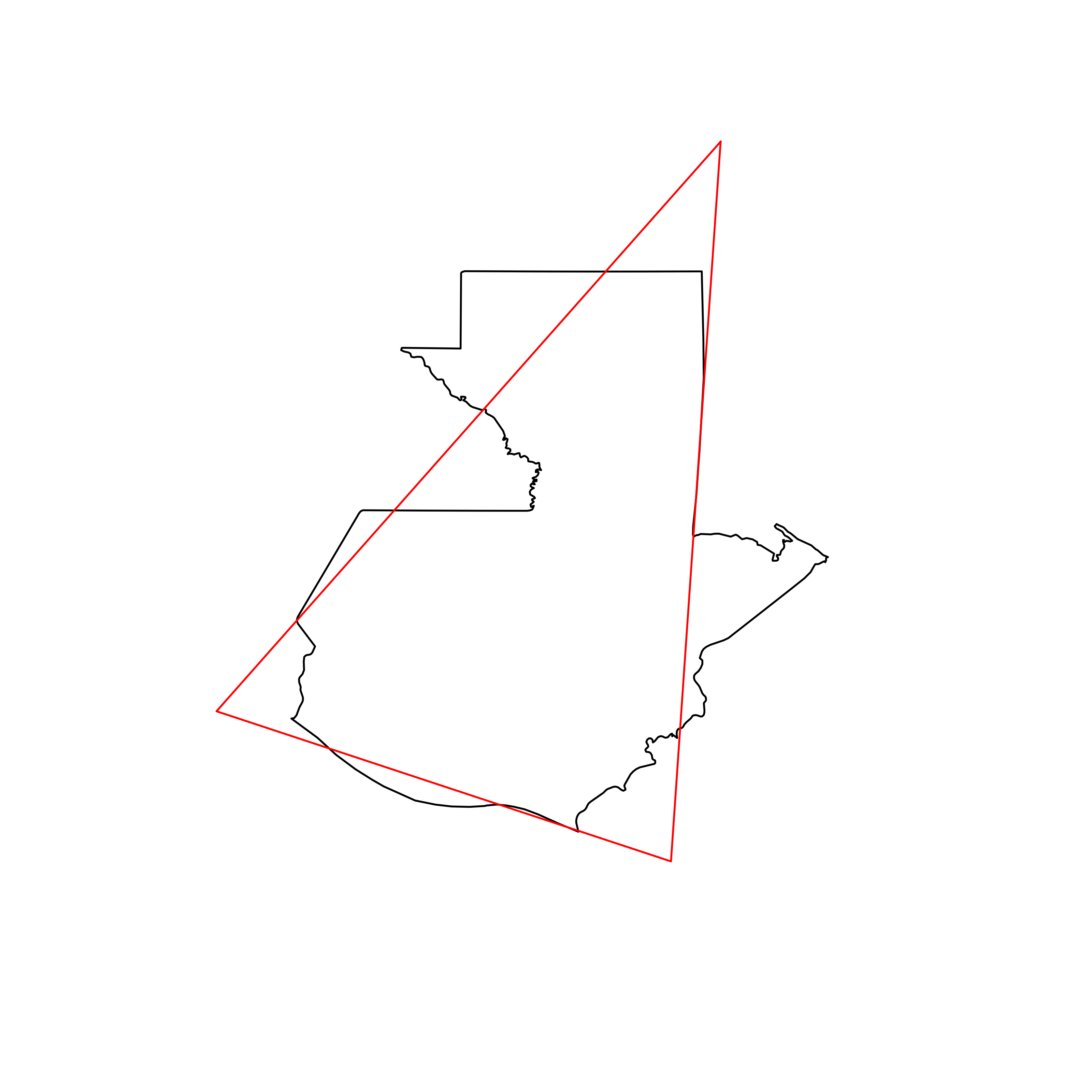 |
| 116 | Turkmenistan | 0.830046 | 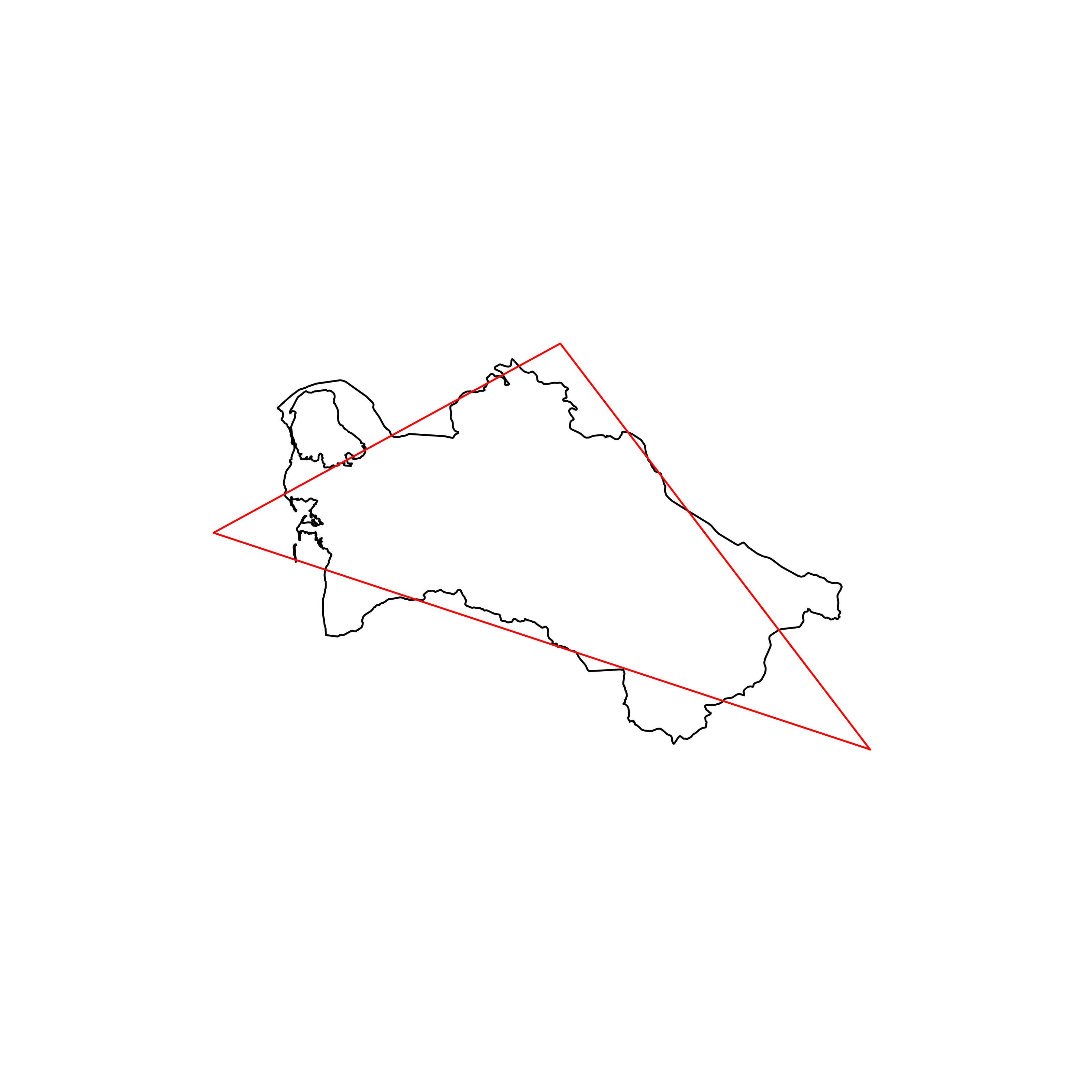 |
| 117 | Peru | 0.829379 | 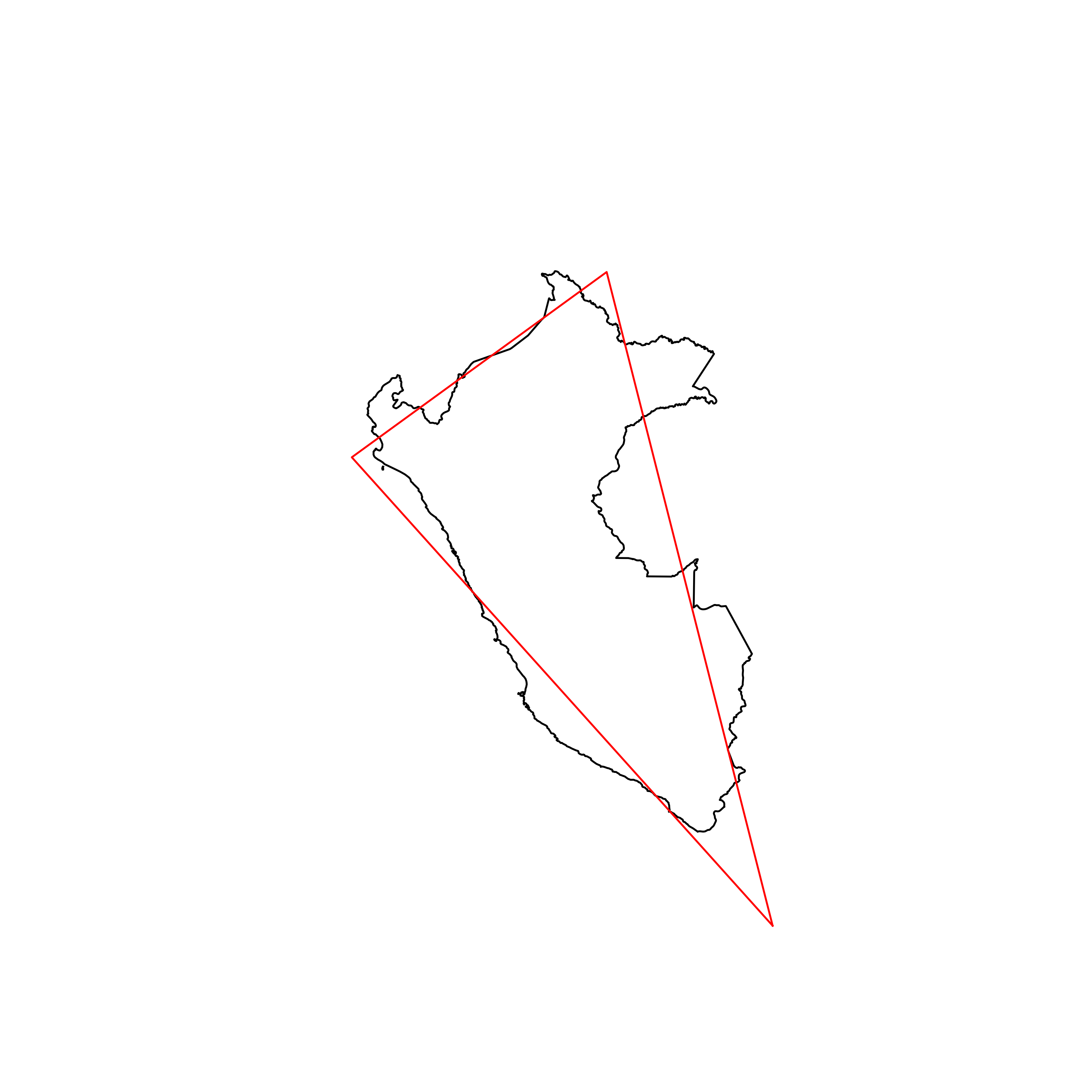 |
| 118 | Moldova | 0.829254 | 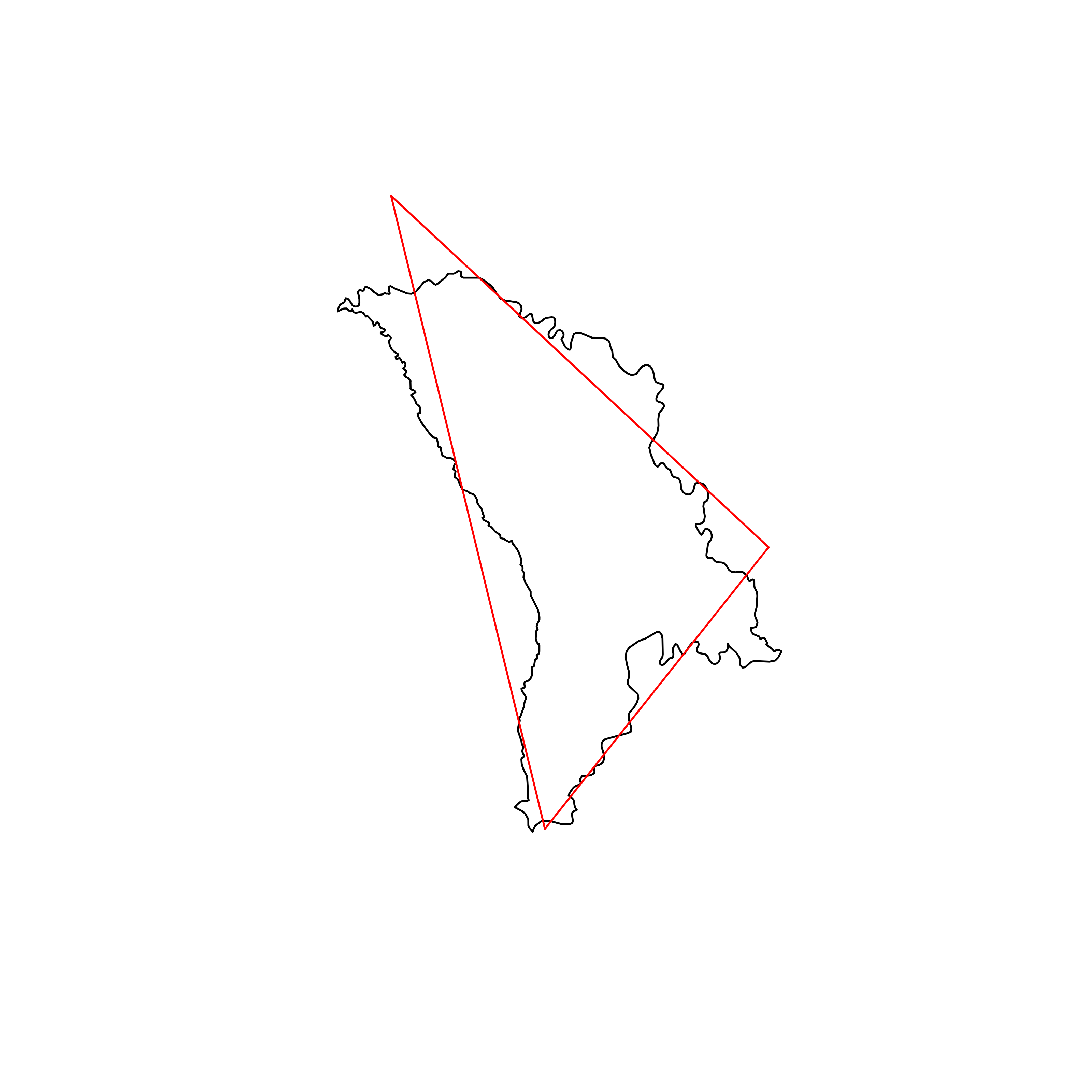 |
| 119 | Myanmar | 0.827051 | 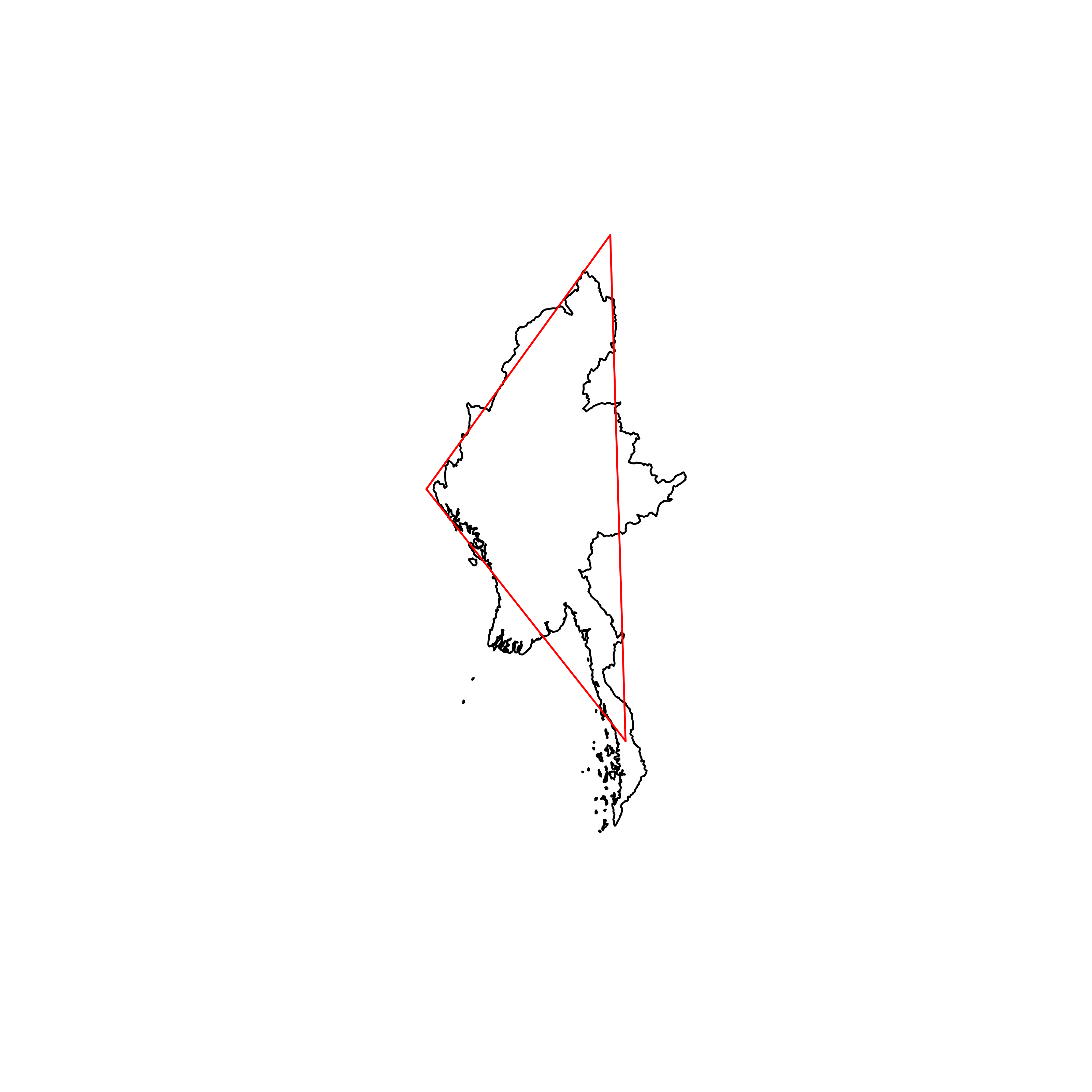 |
| 120 | China | 0.825111 |  |
| 121 | Kazakhstan | 0.825079 | 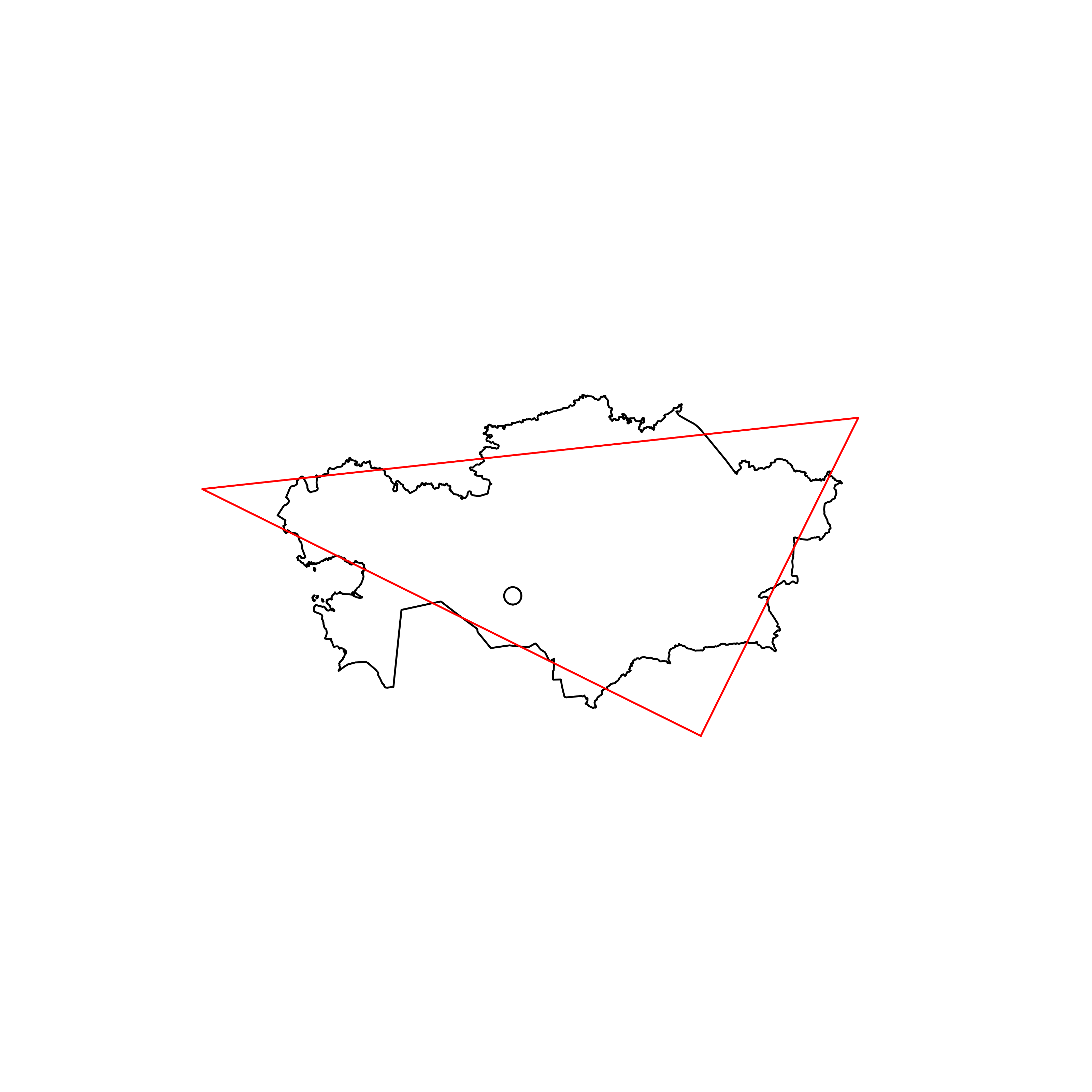 |
| 122 | Saint Vincent and the Grenadines | 0.824970 | 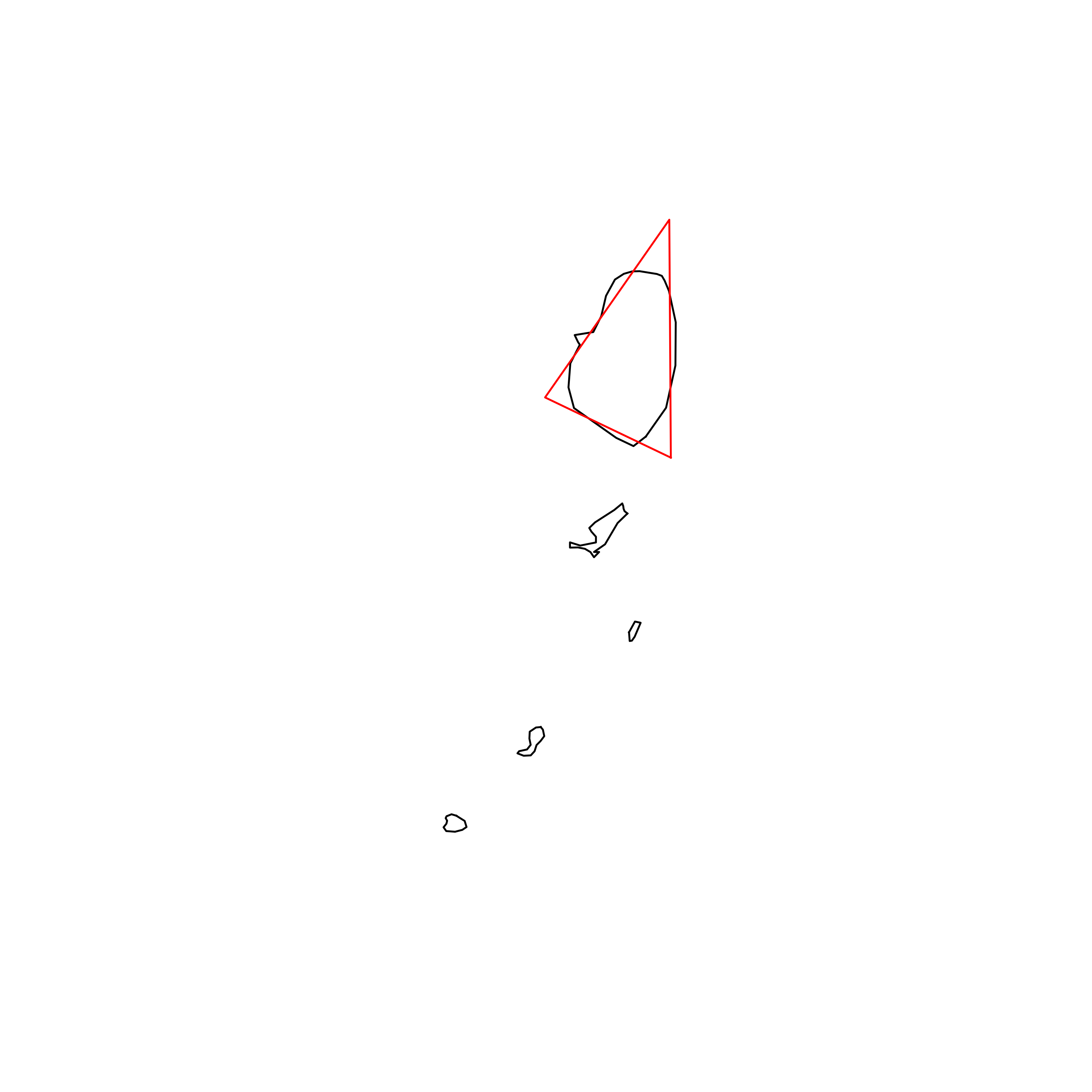 |
| 123 | Latvia | 0.824709 | 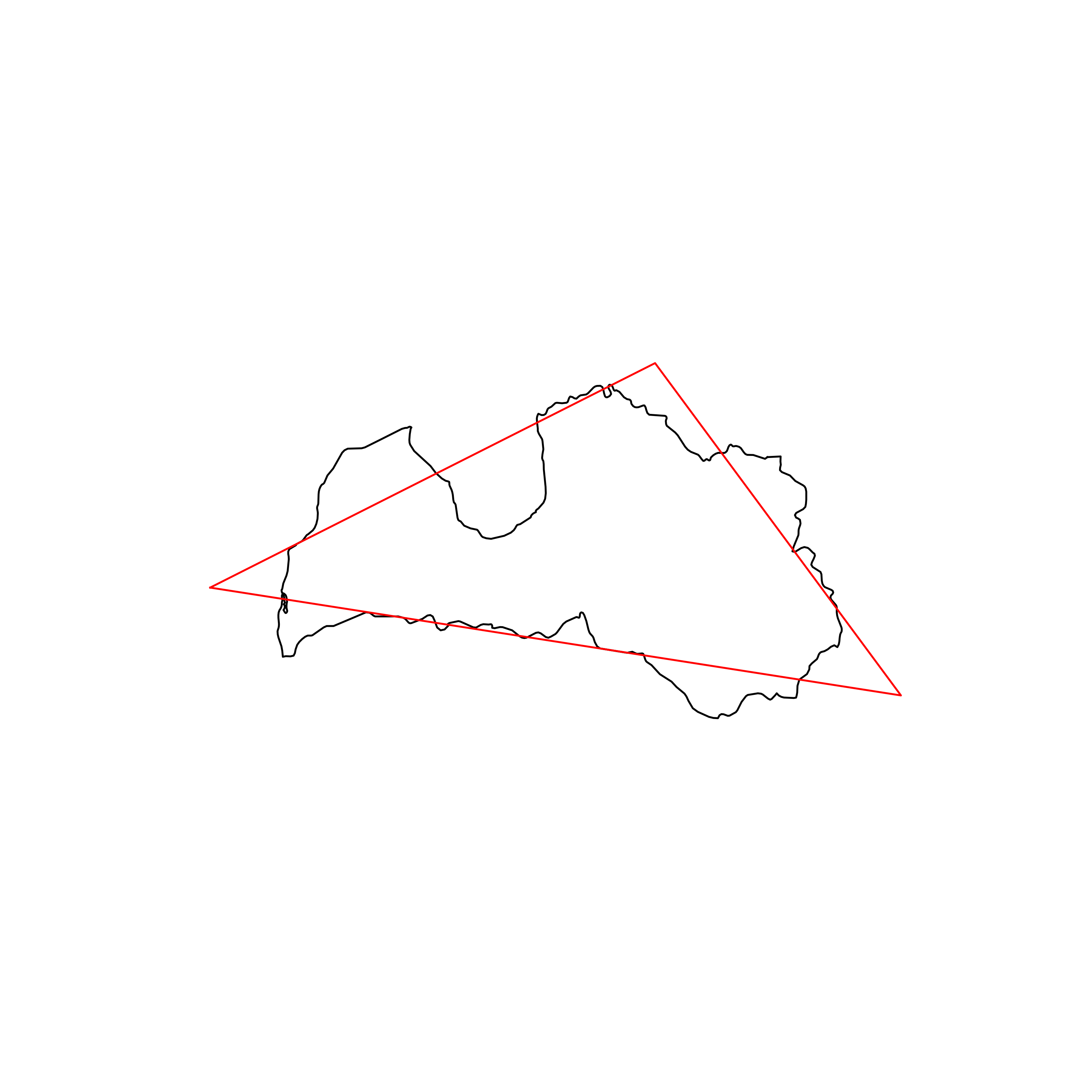 |
| 124 | Djibouti | 0.824624 | 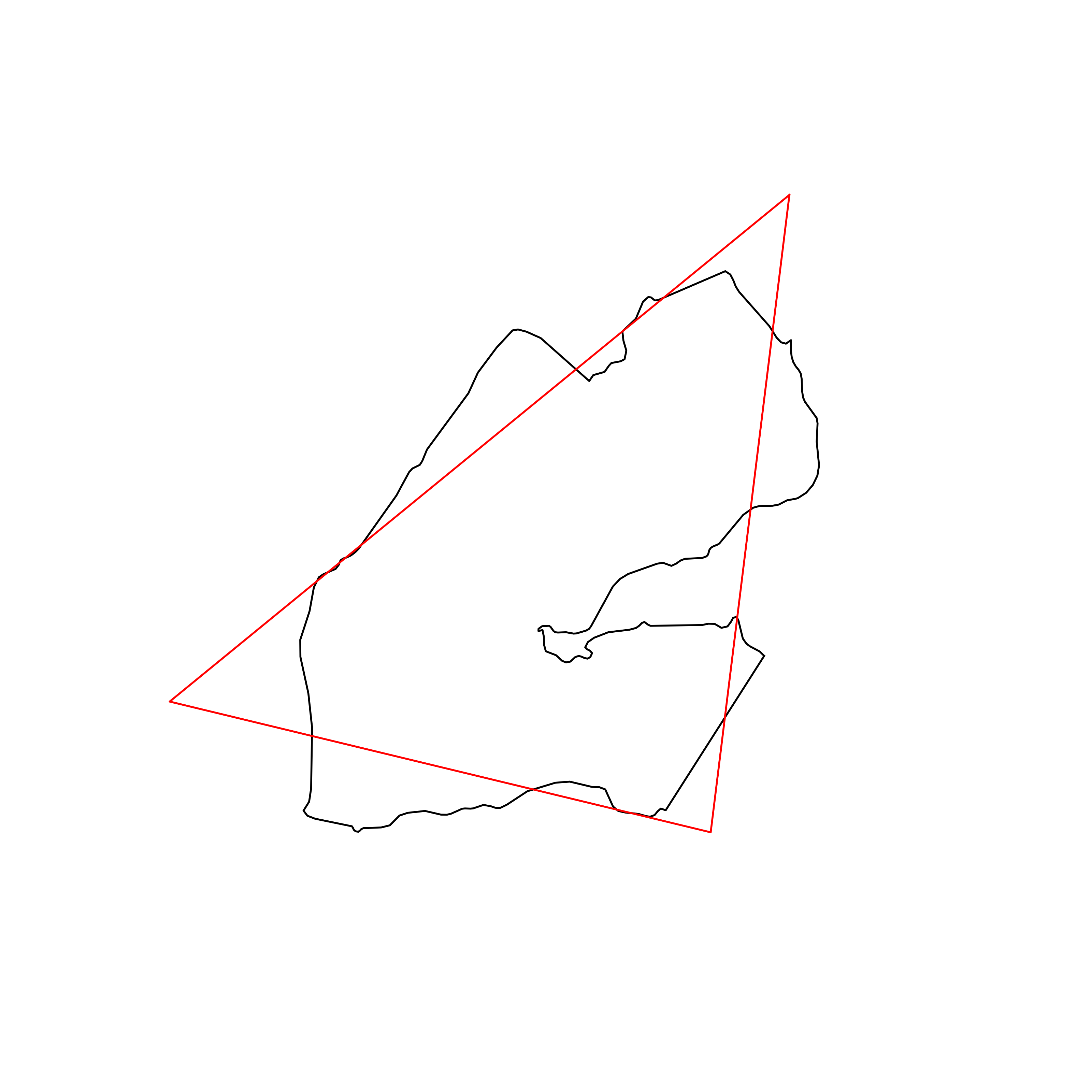 |
| 125 | Equatorial Guinea | 0.819325 | 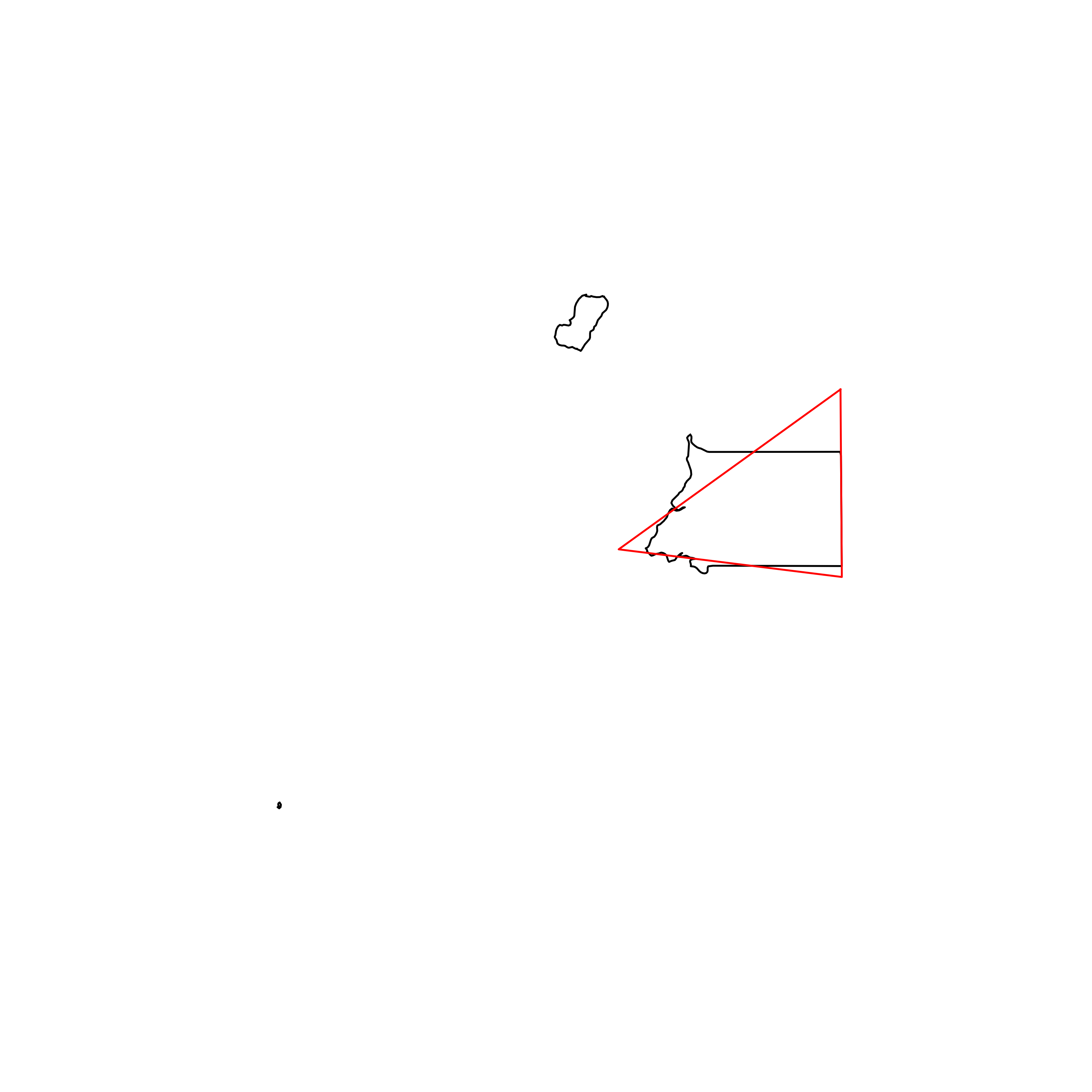 |
| 126 | Jordan | 0.818978 |  |
| 127 | Netherlands | 0.818781 |  |
| 128 | Paraguay | 0.816157 | 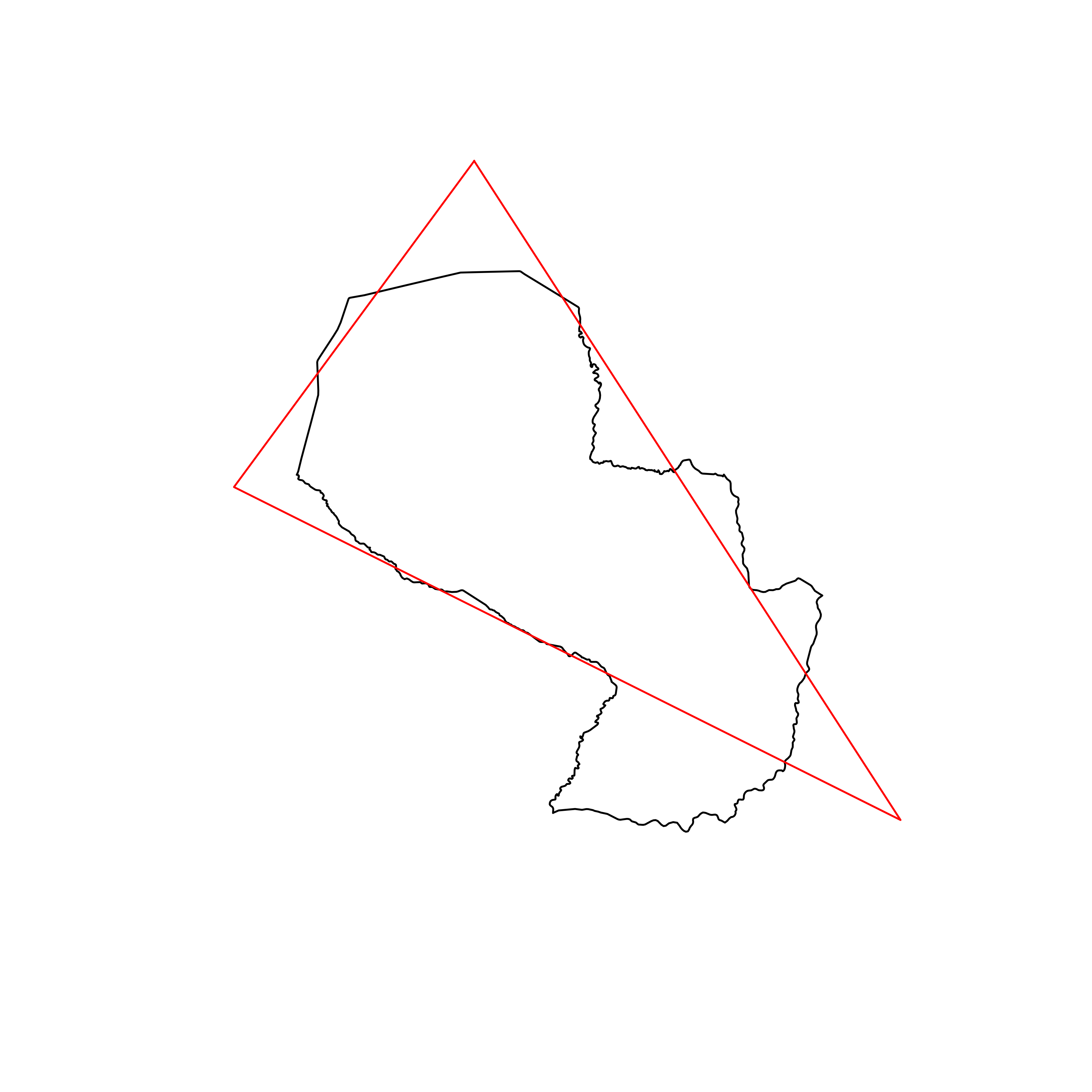 |
| 129 | Guinea-Bissau | 0.815927 | 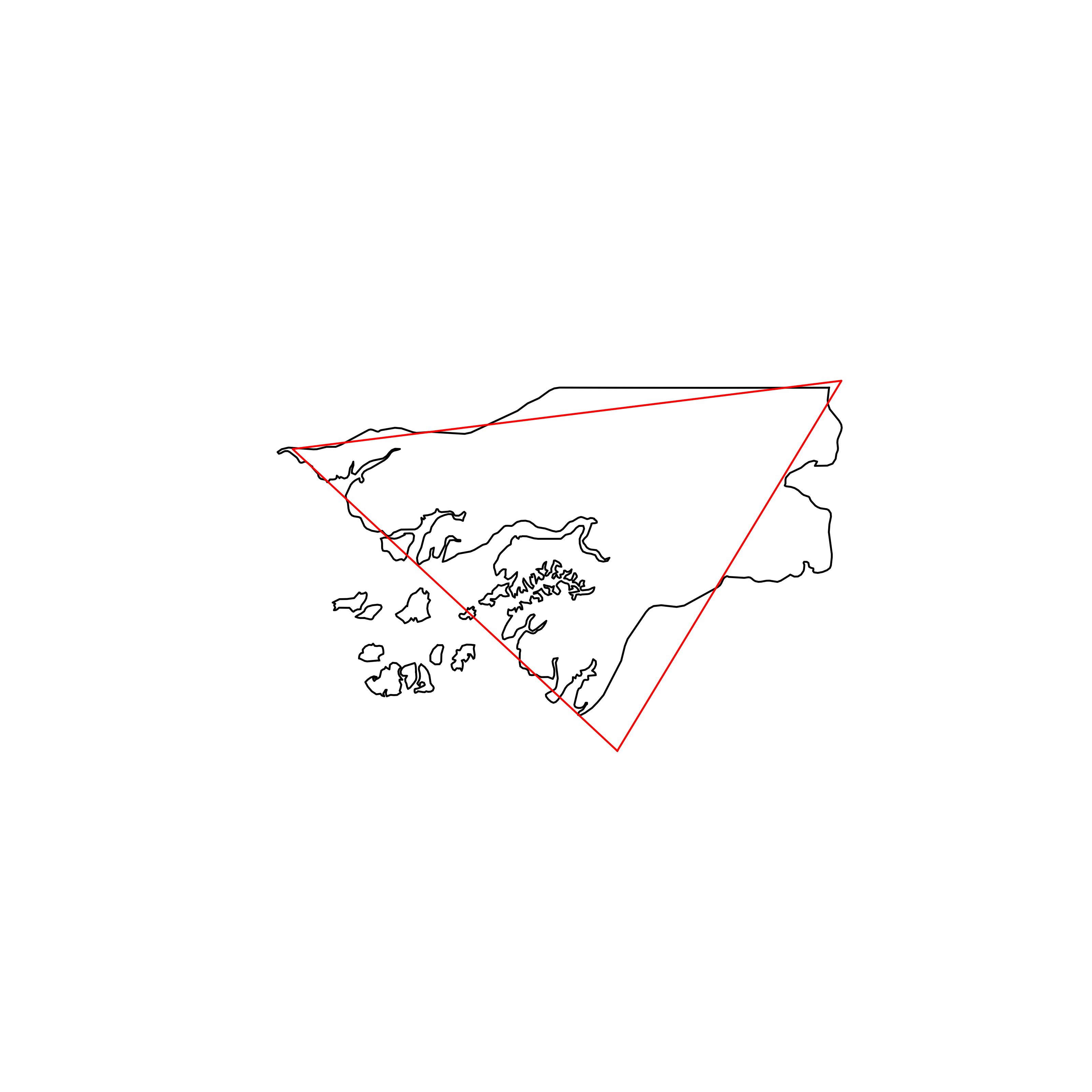 |
| 130 | India | 0.814979 | 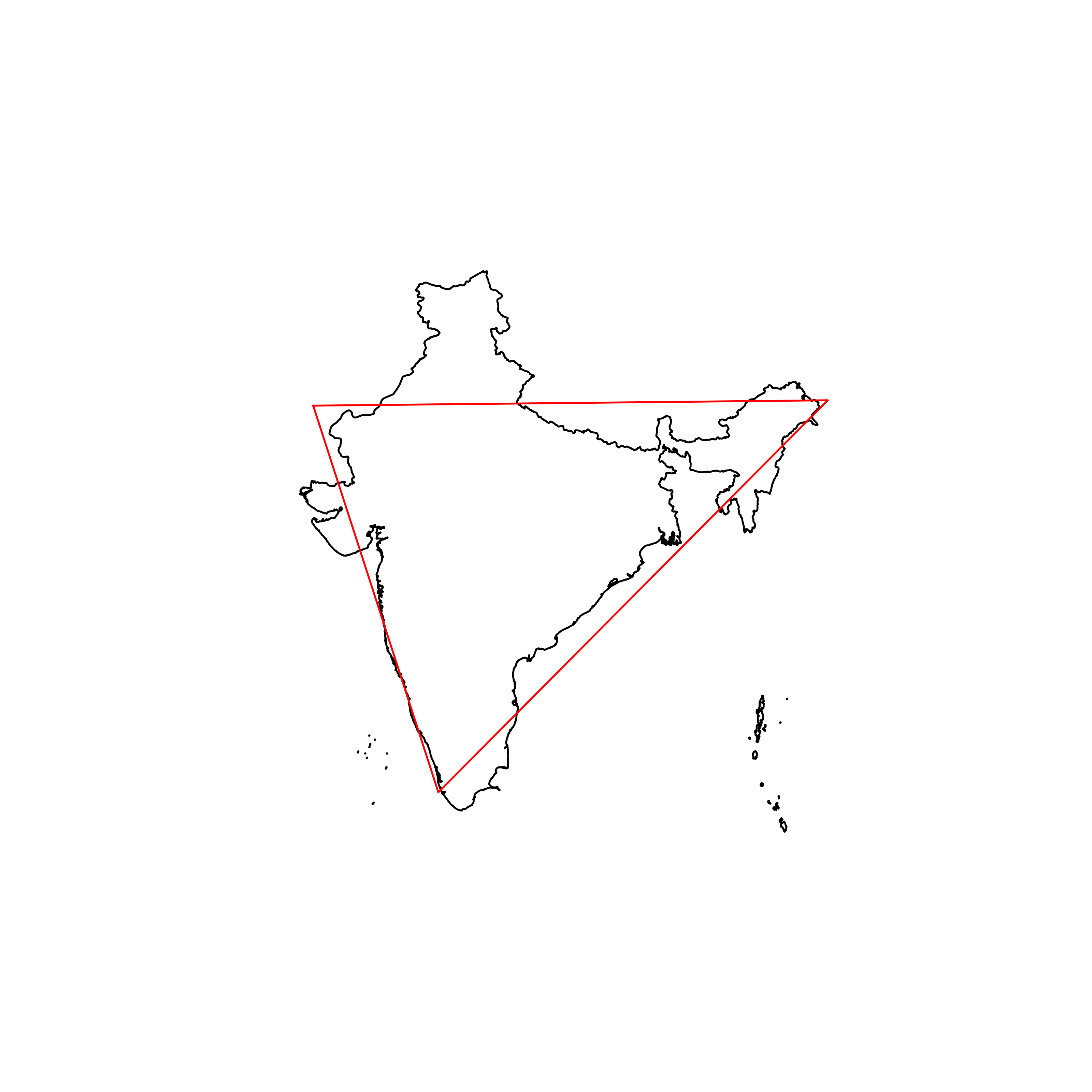 |
| 131 | Costa Rica | 0.814253 | 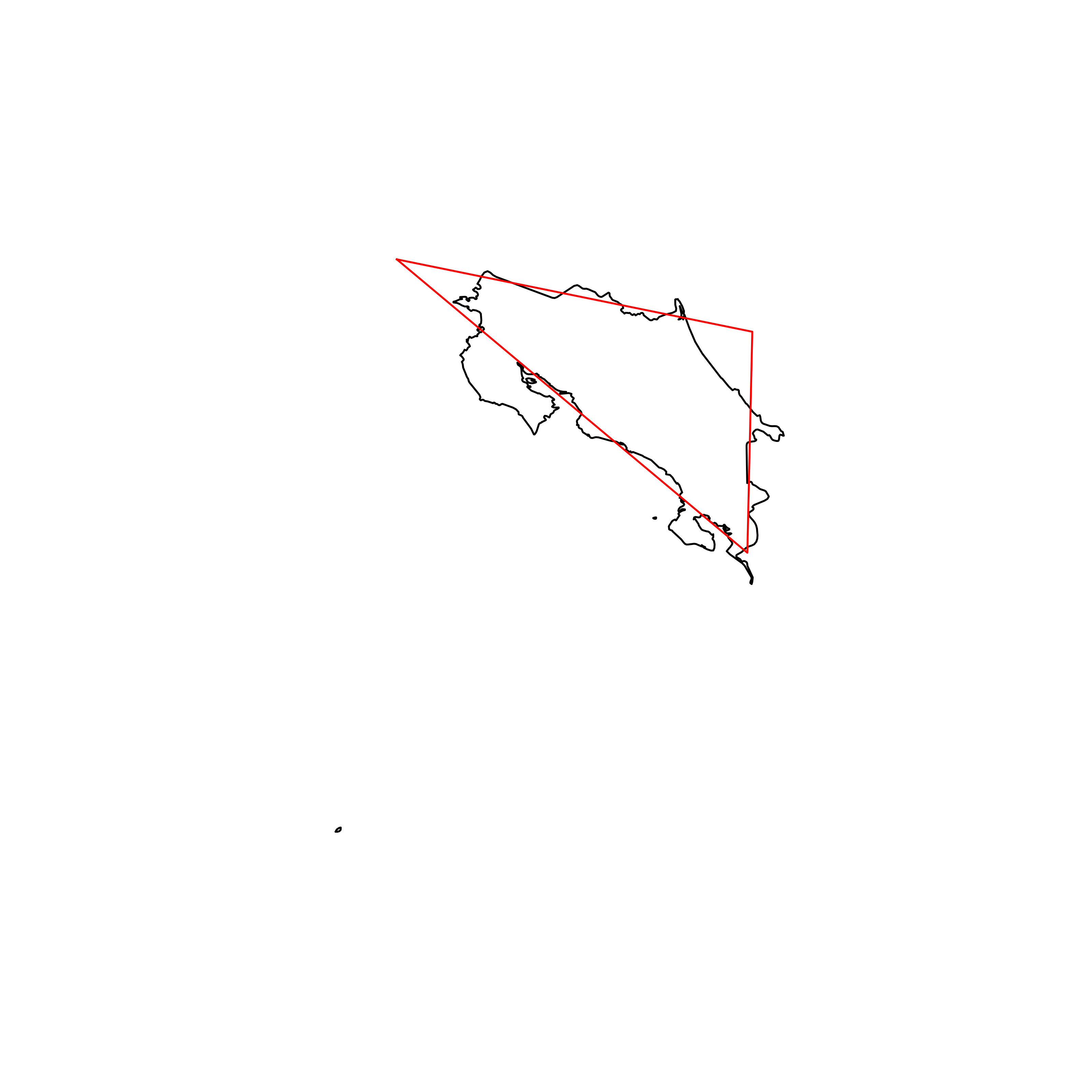 |
| 132 | Ukraine | 0.813770 | 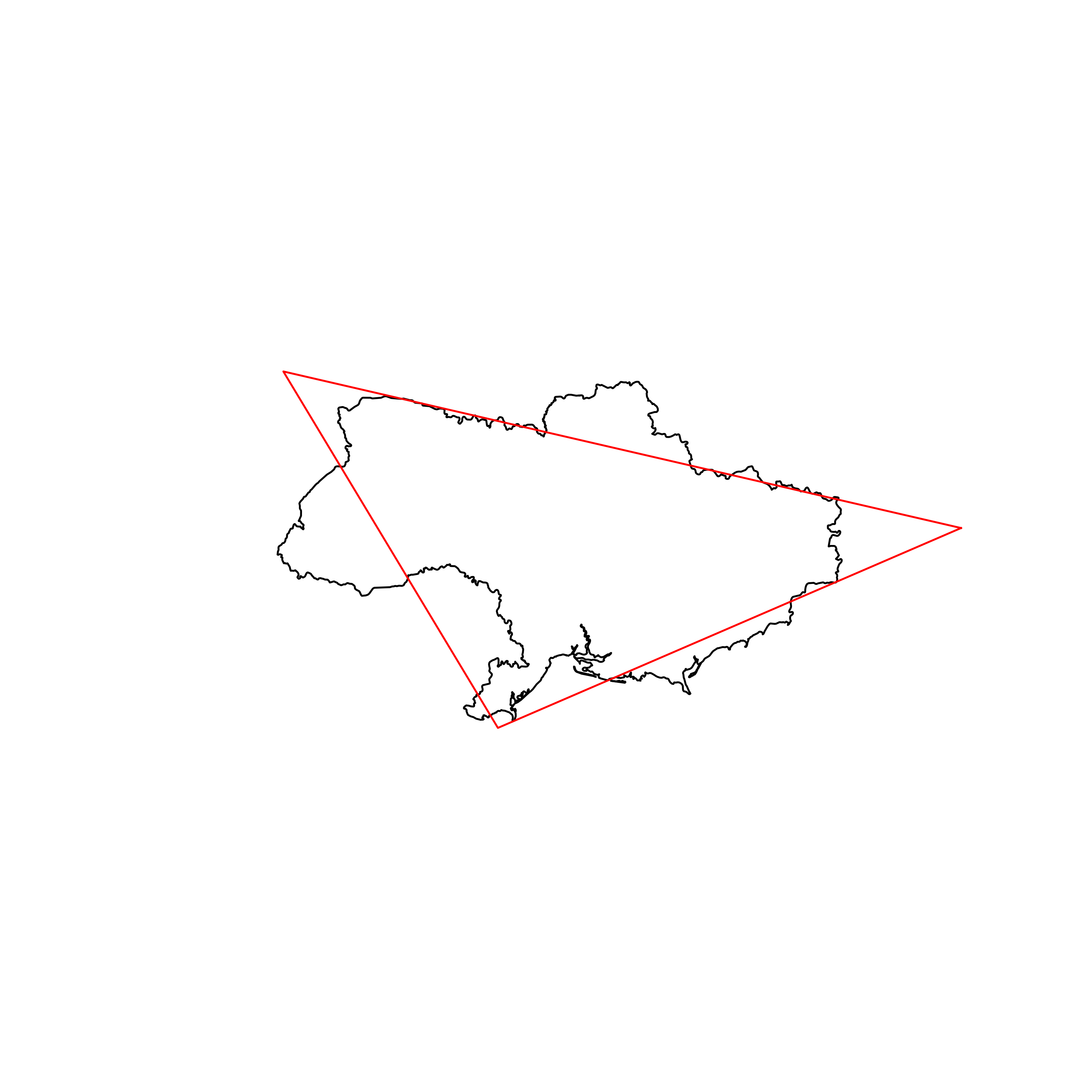 |
| 133 | Colombia | 0.813659 | 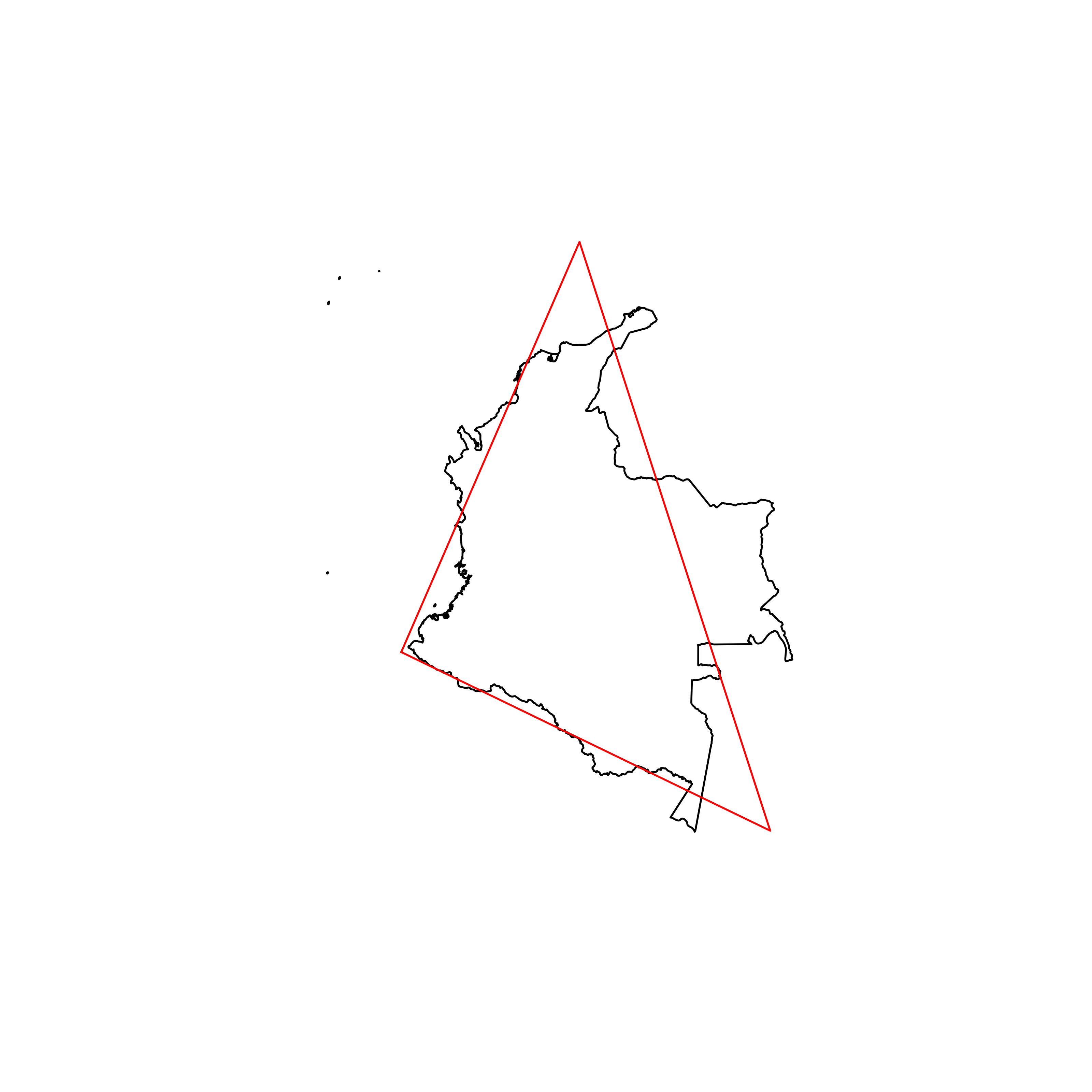 |
| 134 | Grenada | 0.812532 | 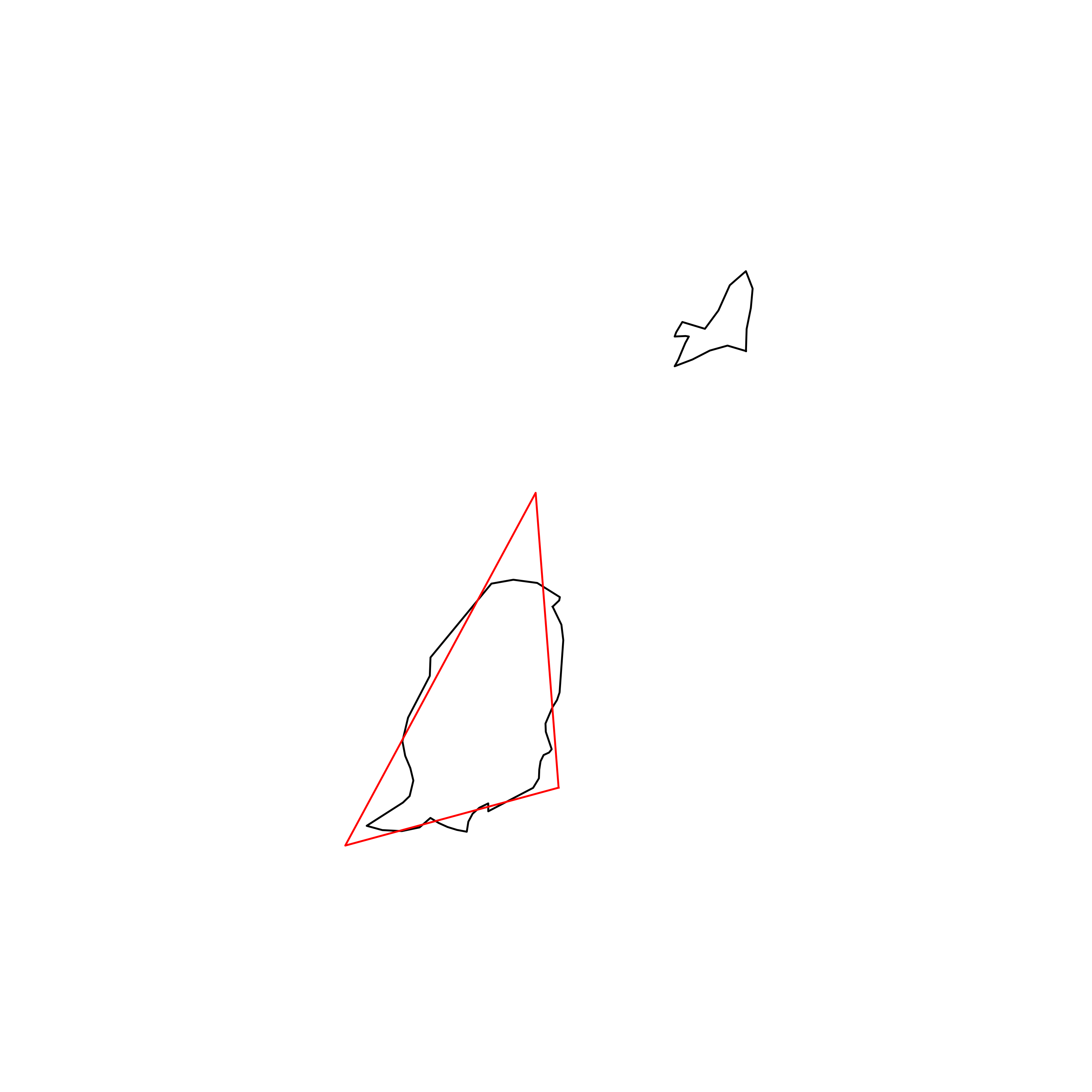 |
| 135 | Egypt | 0.812297 | 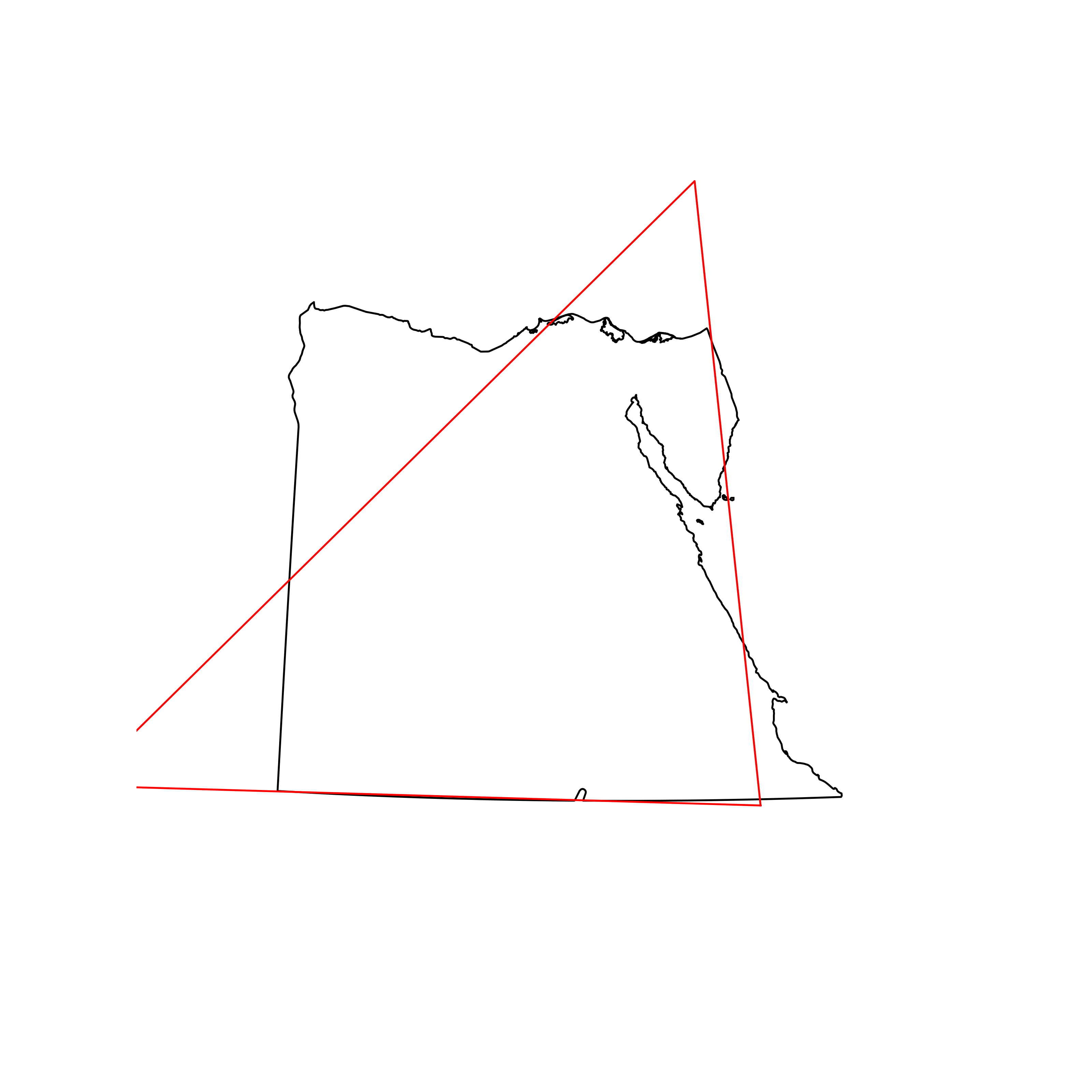 |
| 136 | Portugal | 0.811106 |  |
| 137 | Republic of the Congo | 0.811063 | 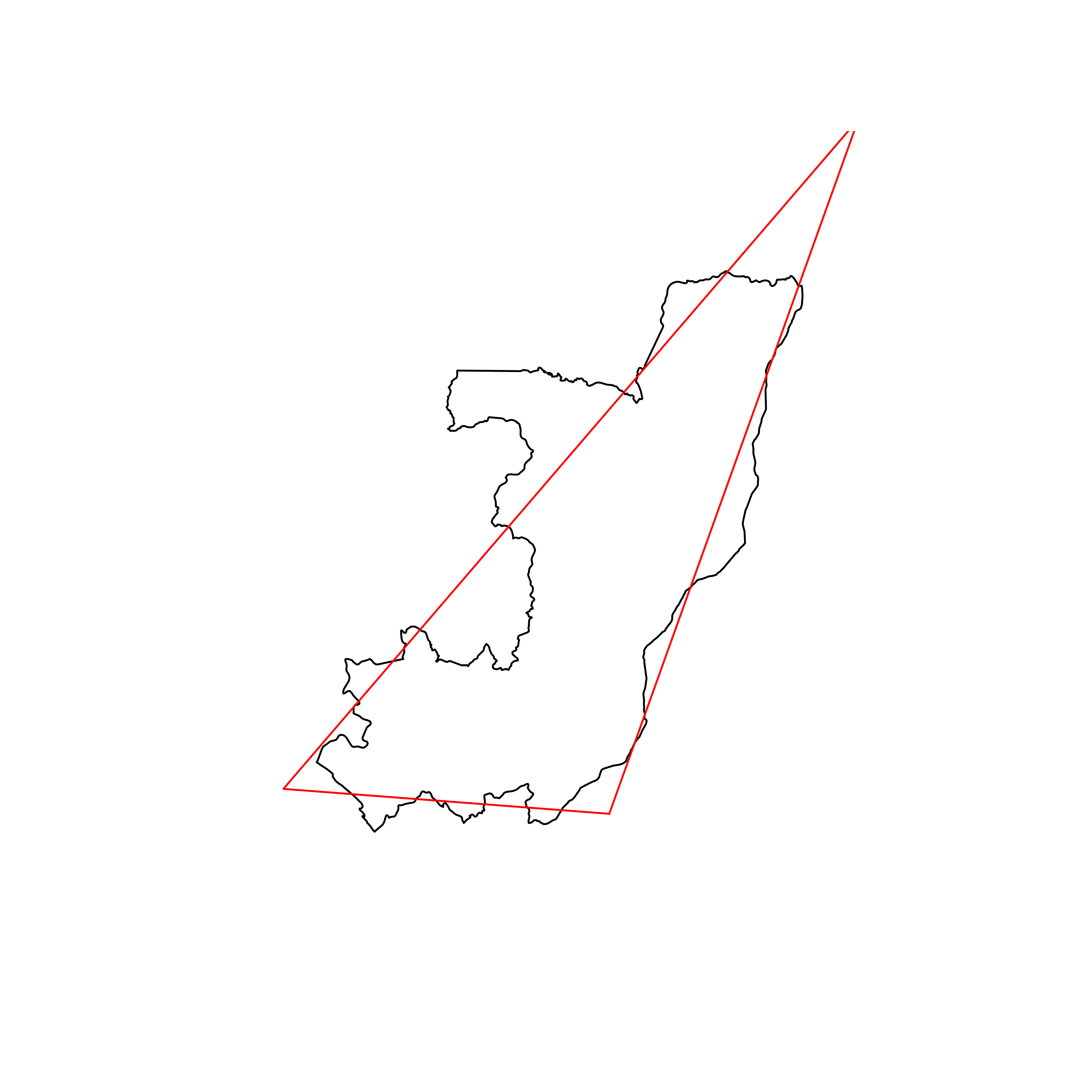 |
| 138 | Tunisia | 0.807452 | 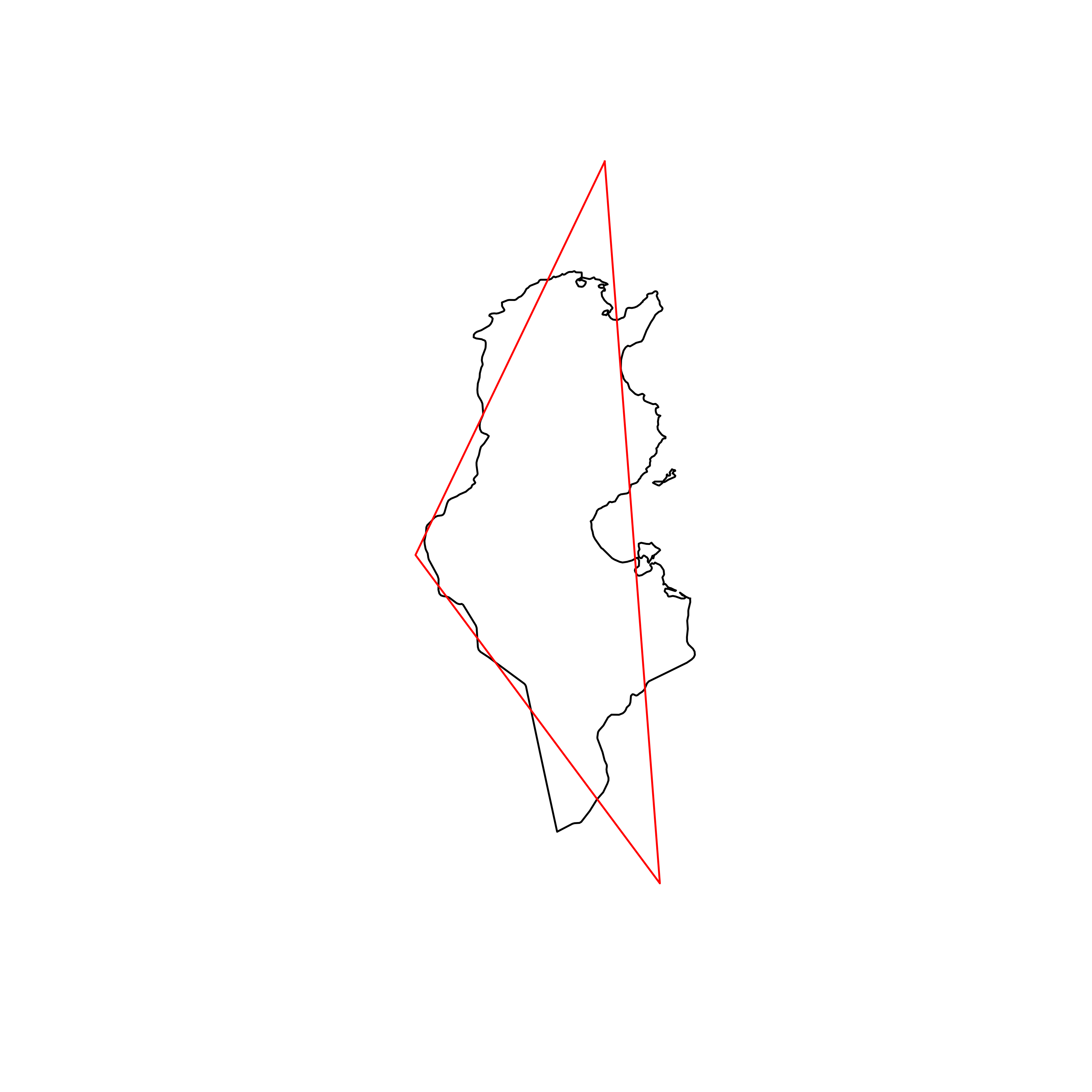 |
| 139 | Trinidad and Tobago | 0.804956 | 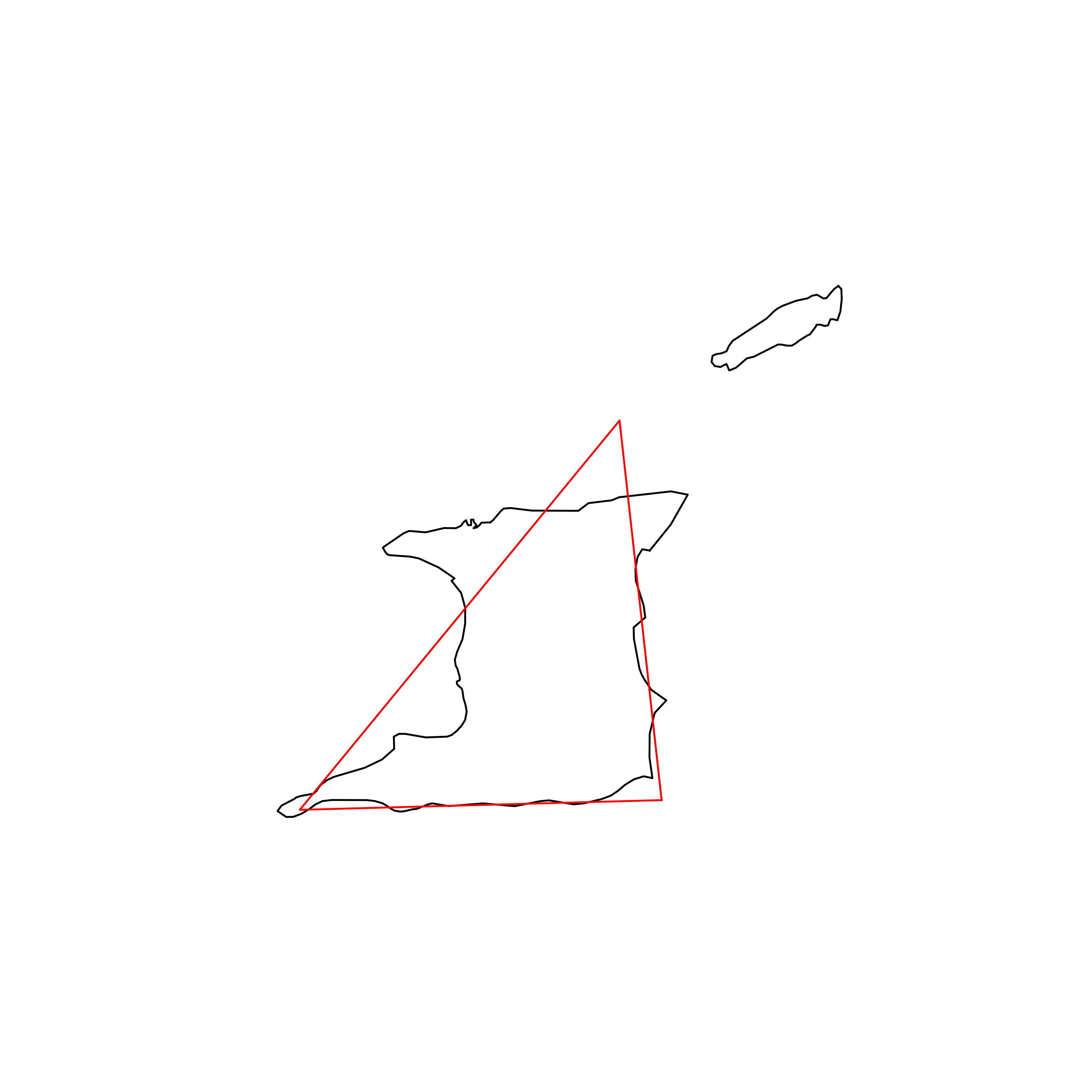 |
| 140 | Sweden | 0.804381 | 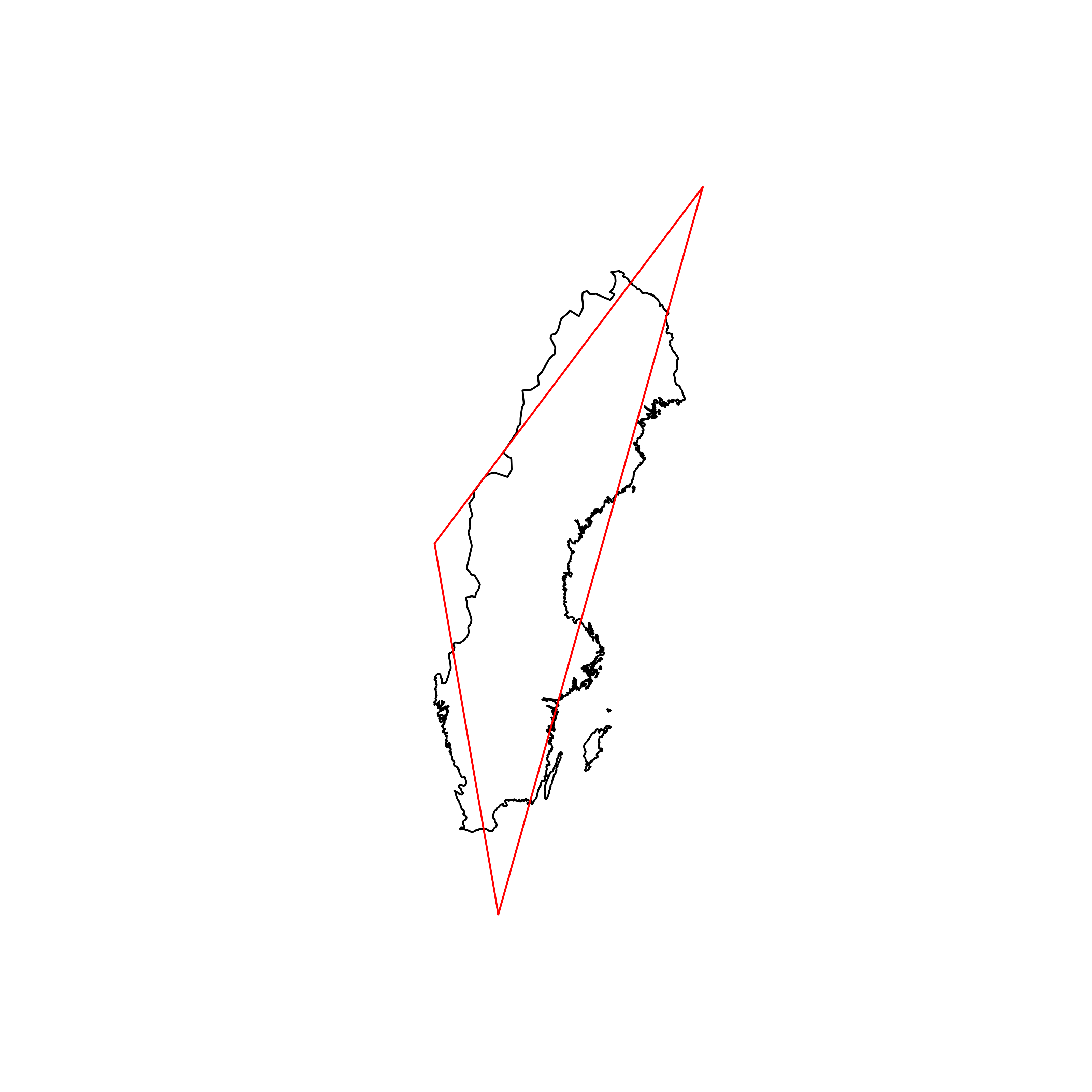 |
| 141 | Somalia | 0.802796 | 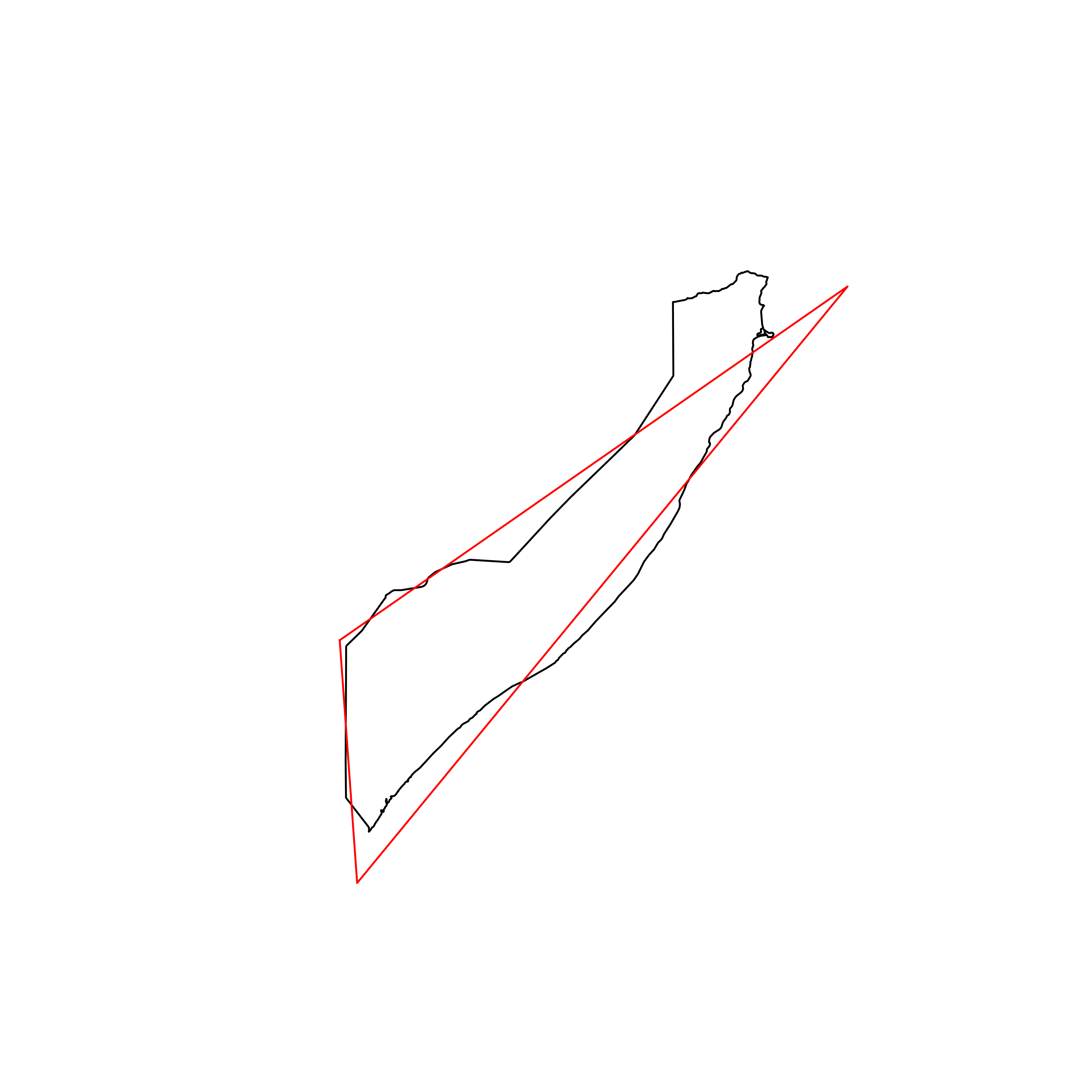 |
| 142 | Malawi | 0.802539 | 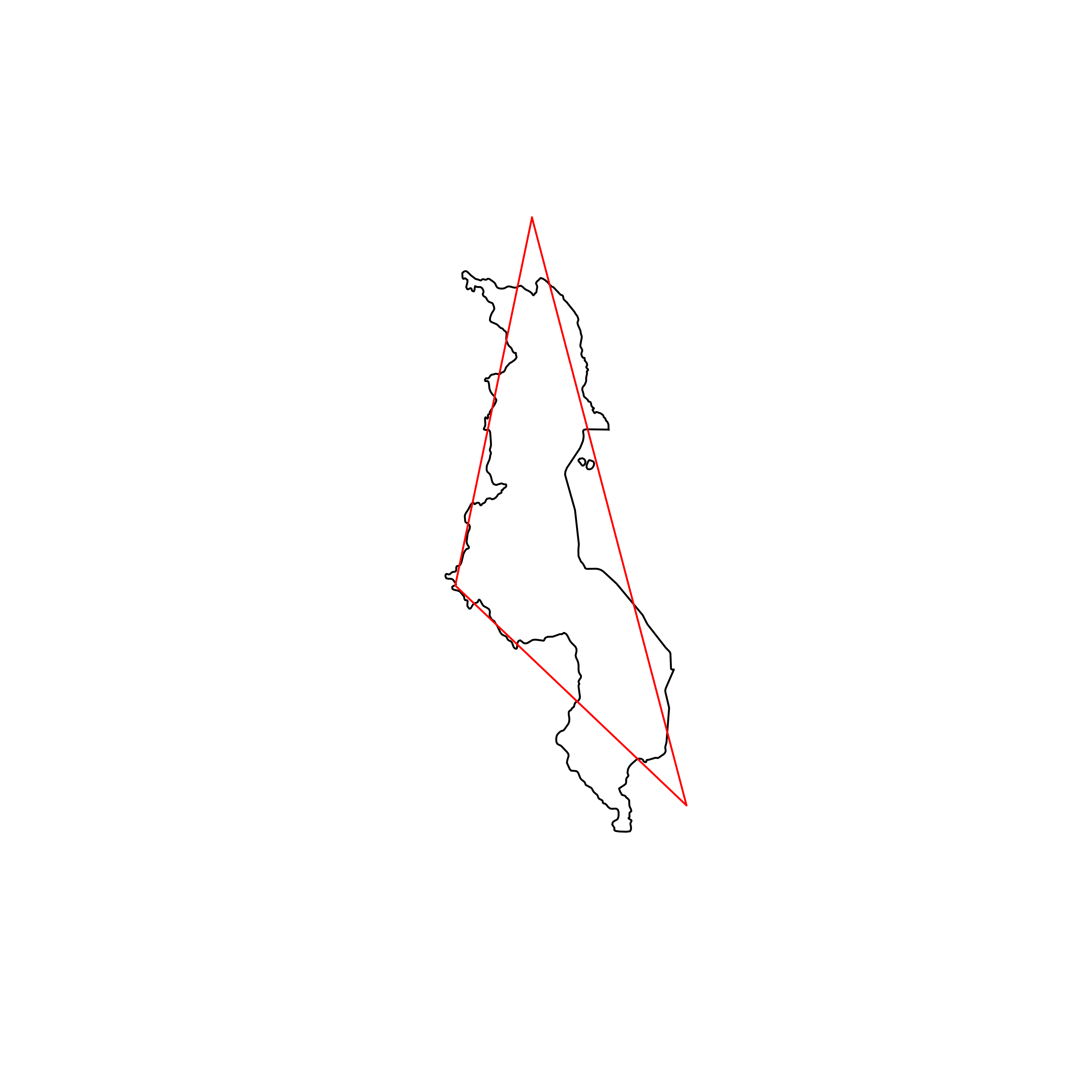 |
| 143 | Russia | 0.800247 | 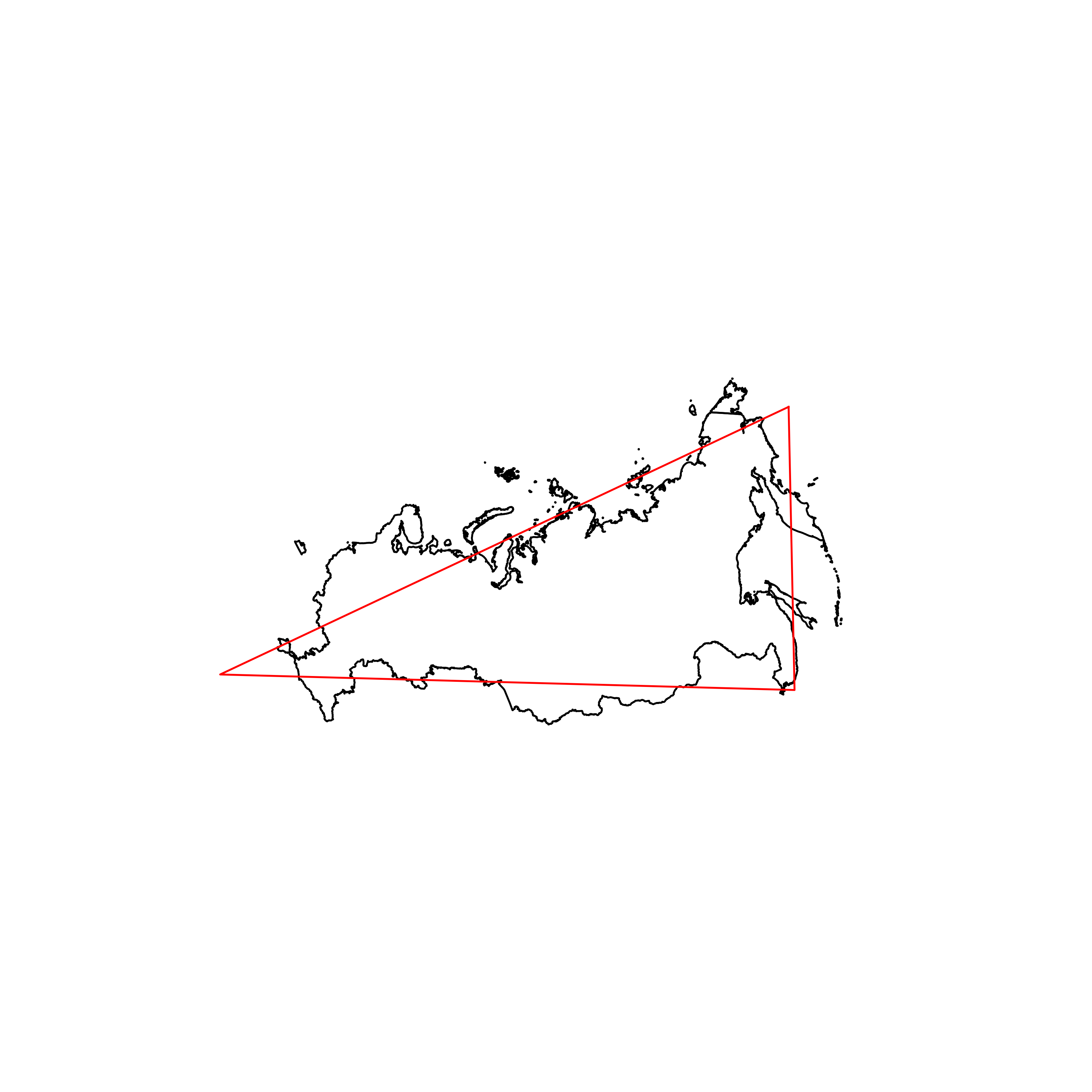 |
| 144 | Zambia | 0.799161 | 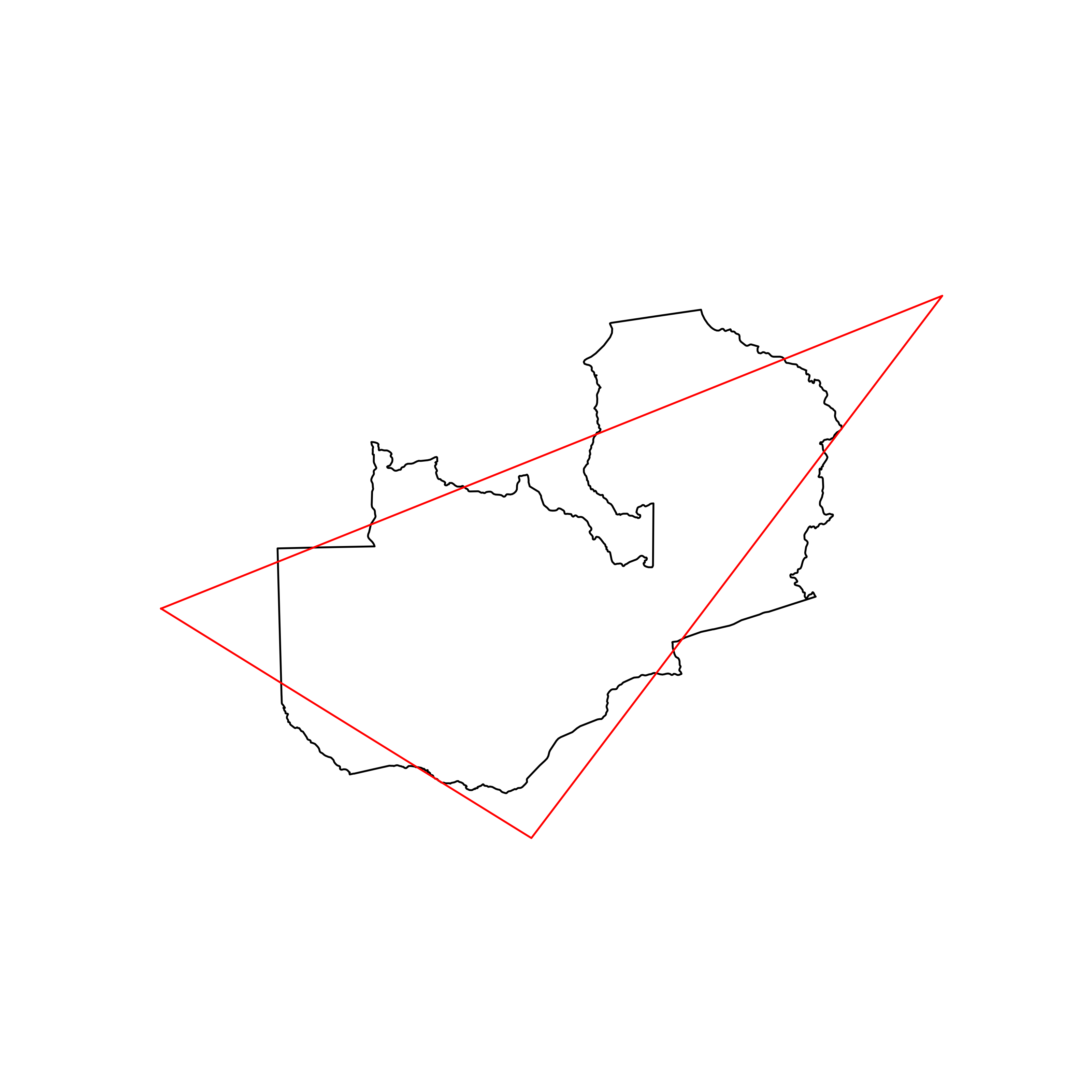 |
| 145 | Guyana | 0.798601 | 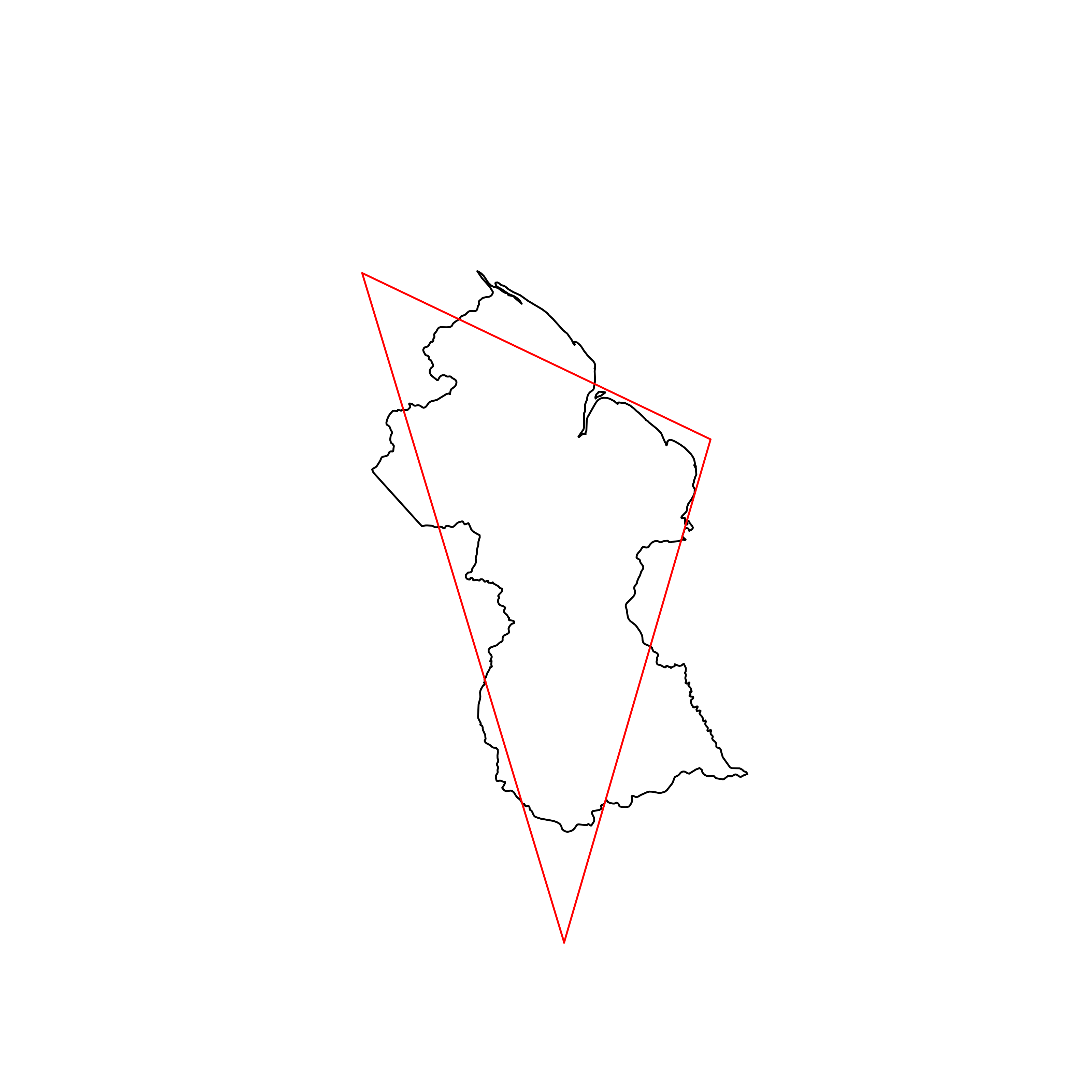 |
| 146 | Azerbaijan | 0.796271 | 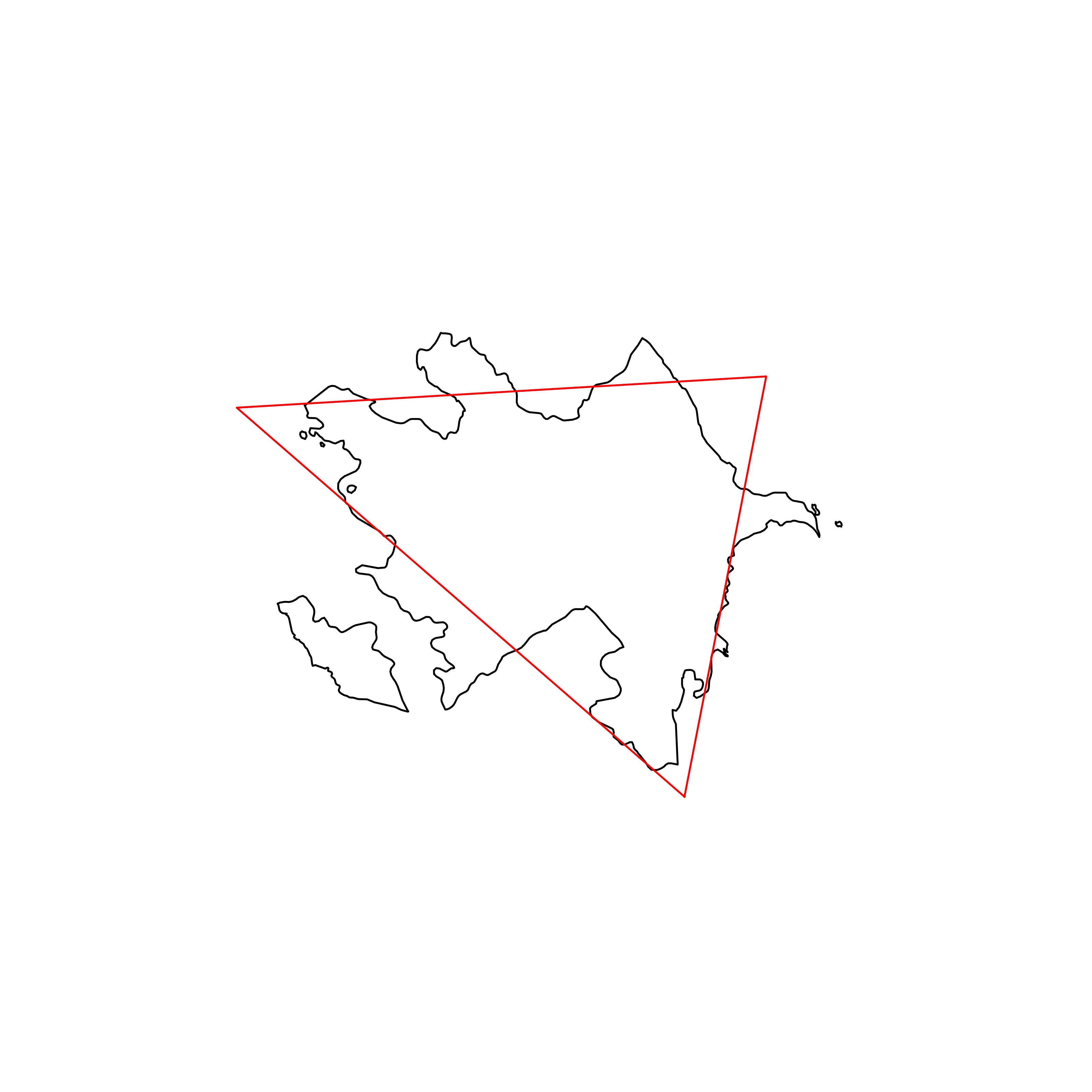 |
| 147 | Uzbekistan | 0.795089 |  |
| 148 | Thailand | 0.794683 | 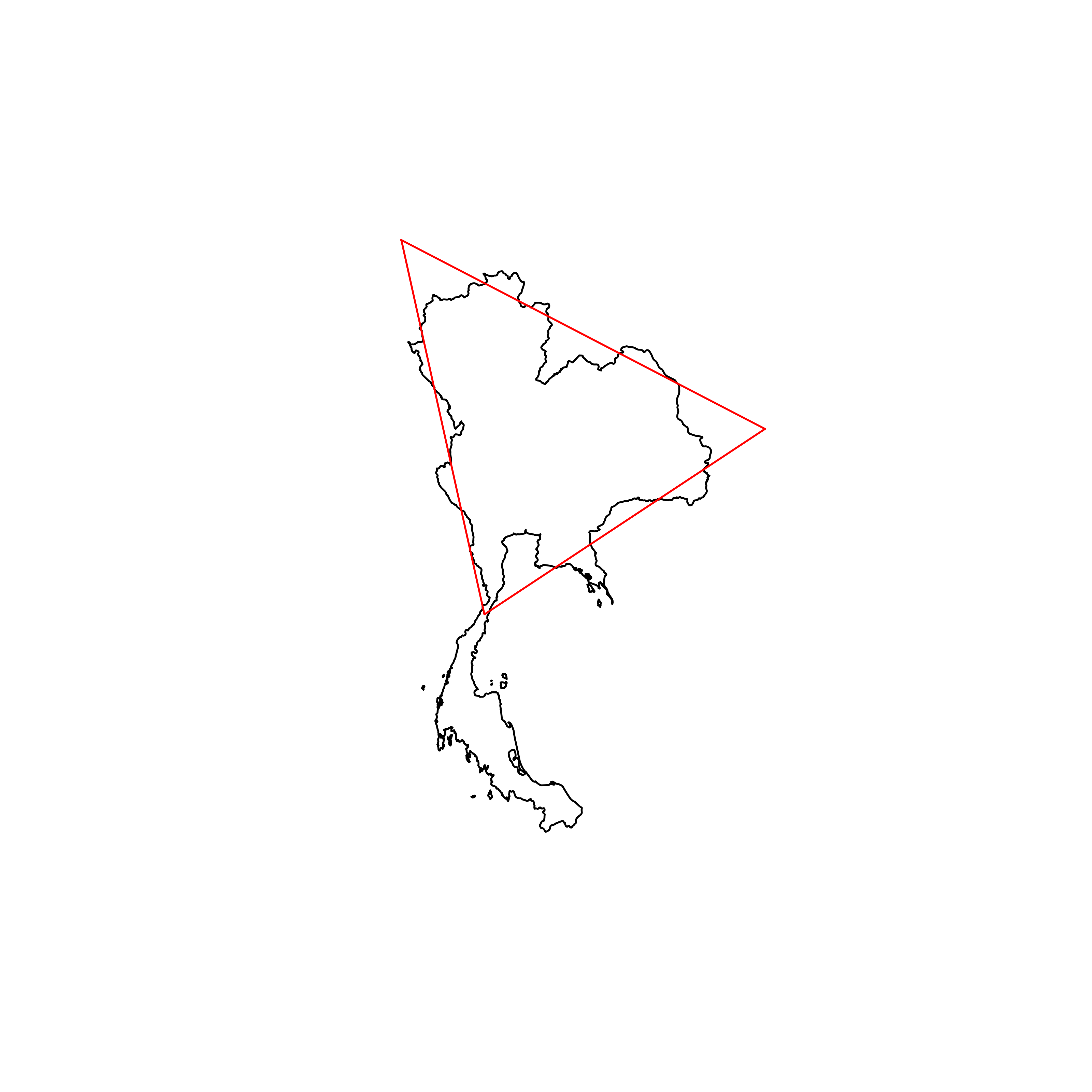 |
| 149 | São Tomé and Principe | 0.793244 |  |
| 150 | Bangladesh | 0.791780 |  |
| 151 | United Kingdom | 0.791691 | 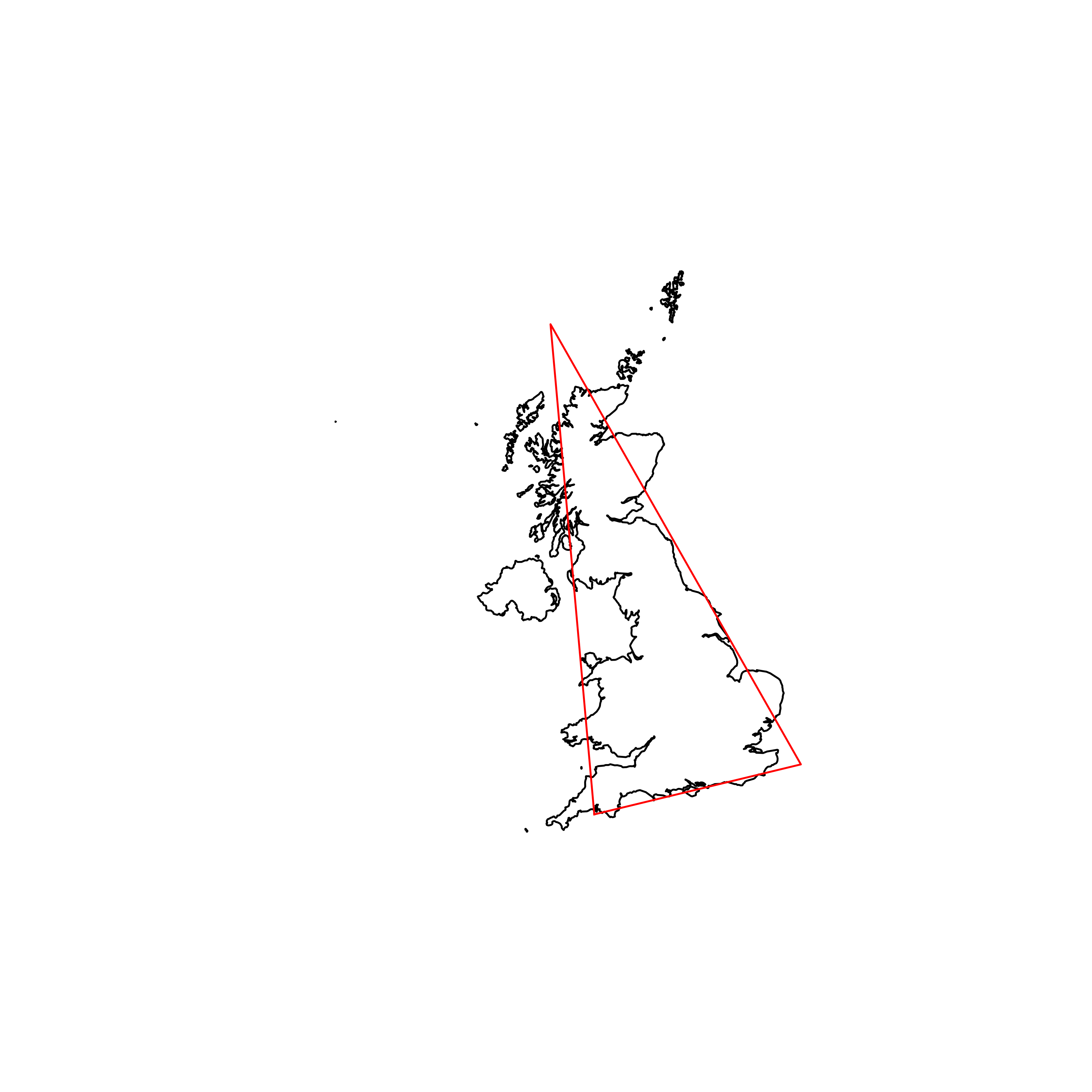 |
| 152 | Eritrea | 0.789674 | 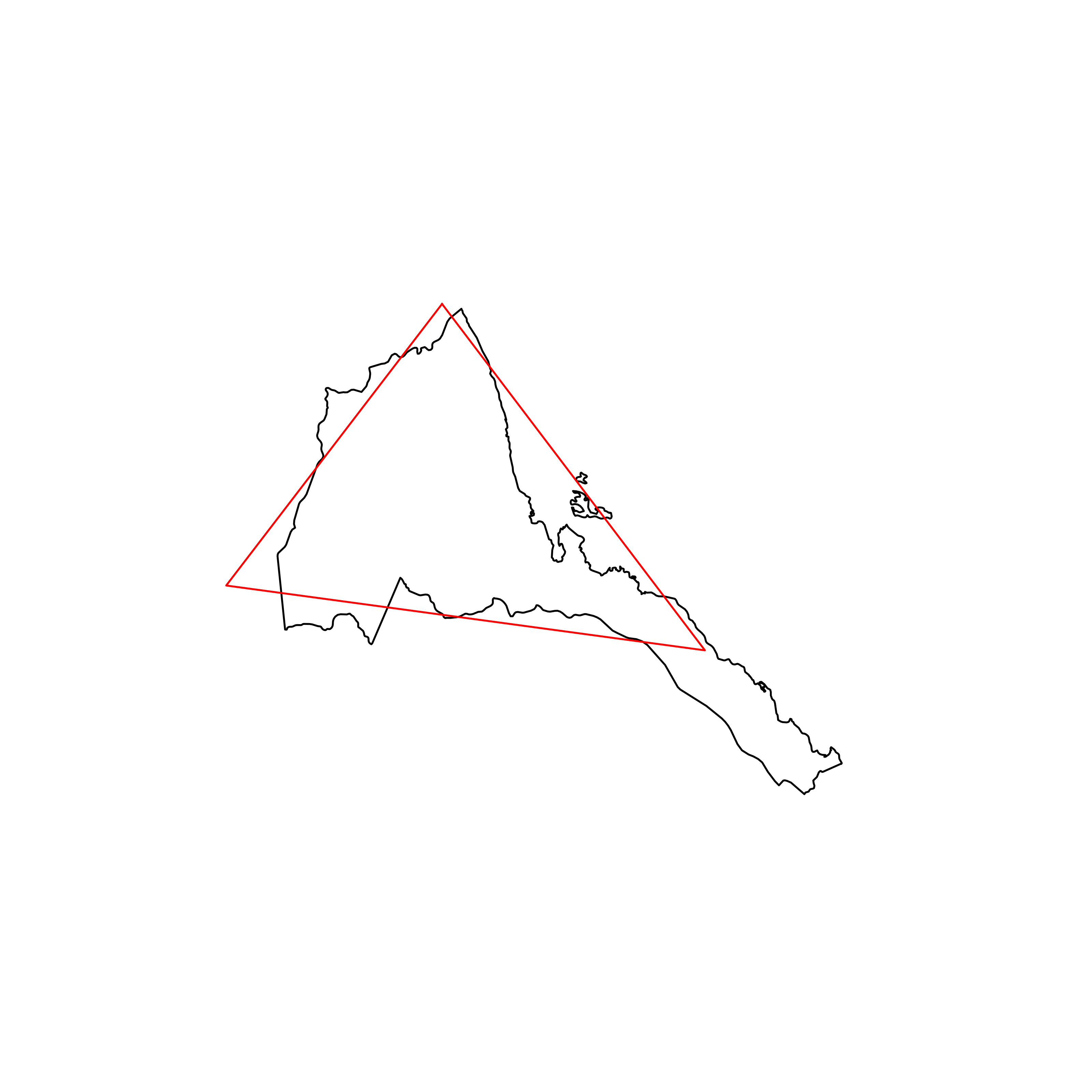 |
| 153 | Malta | 0.786289 | 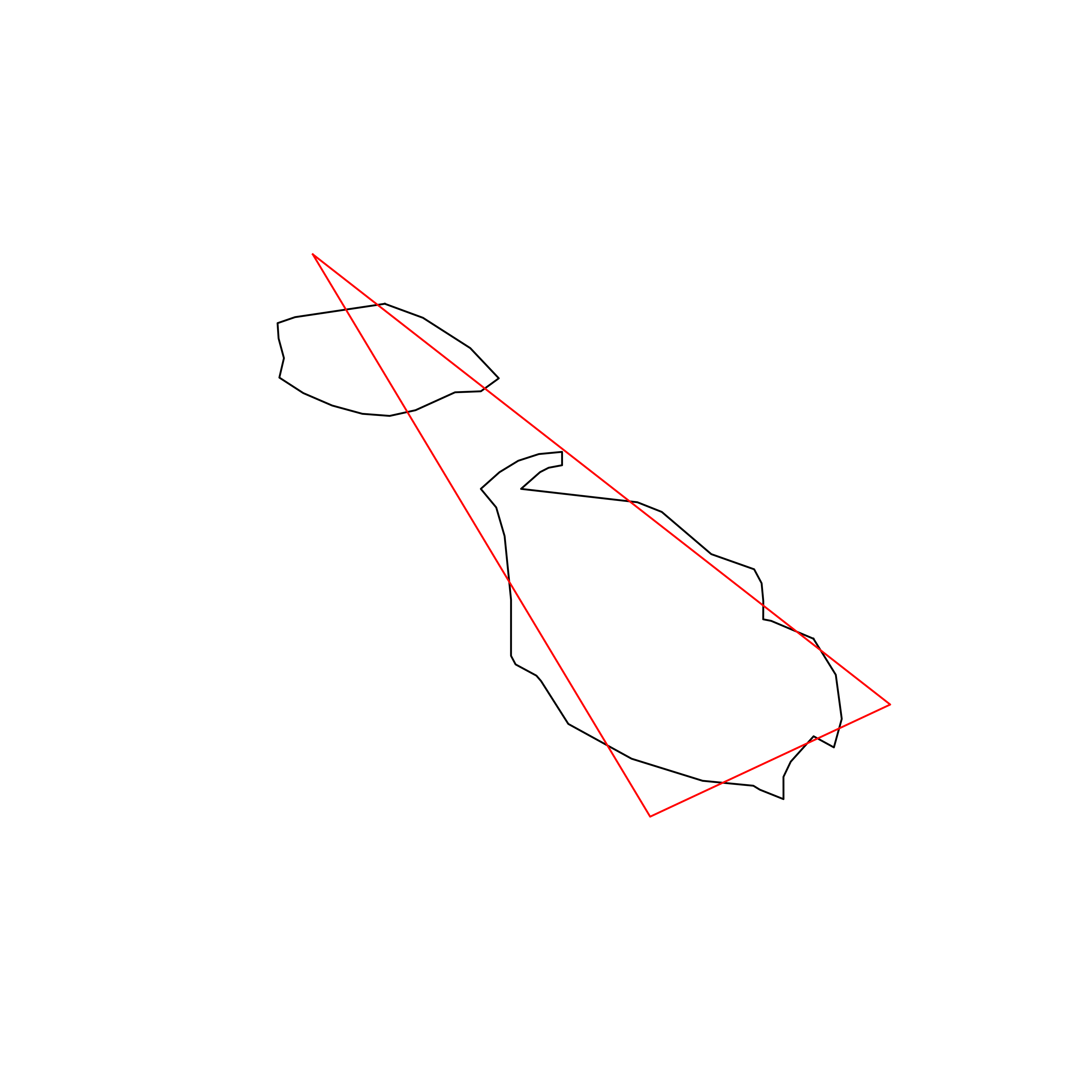 |
| 154 | Mozambique | 0.786196 | 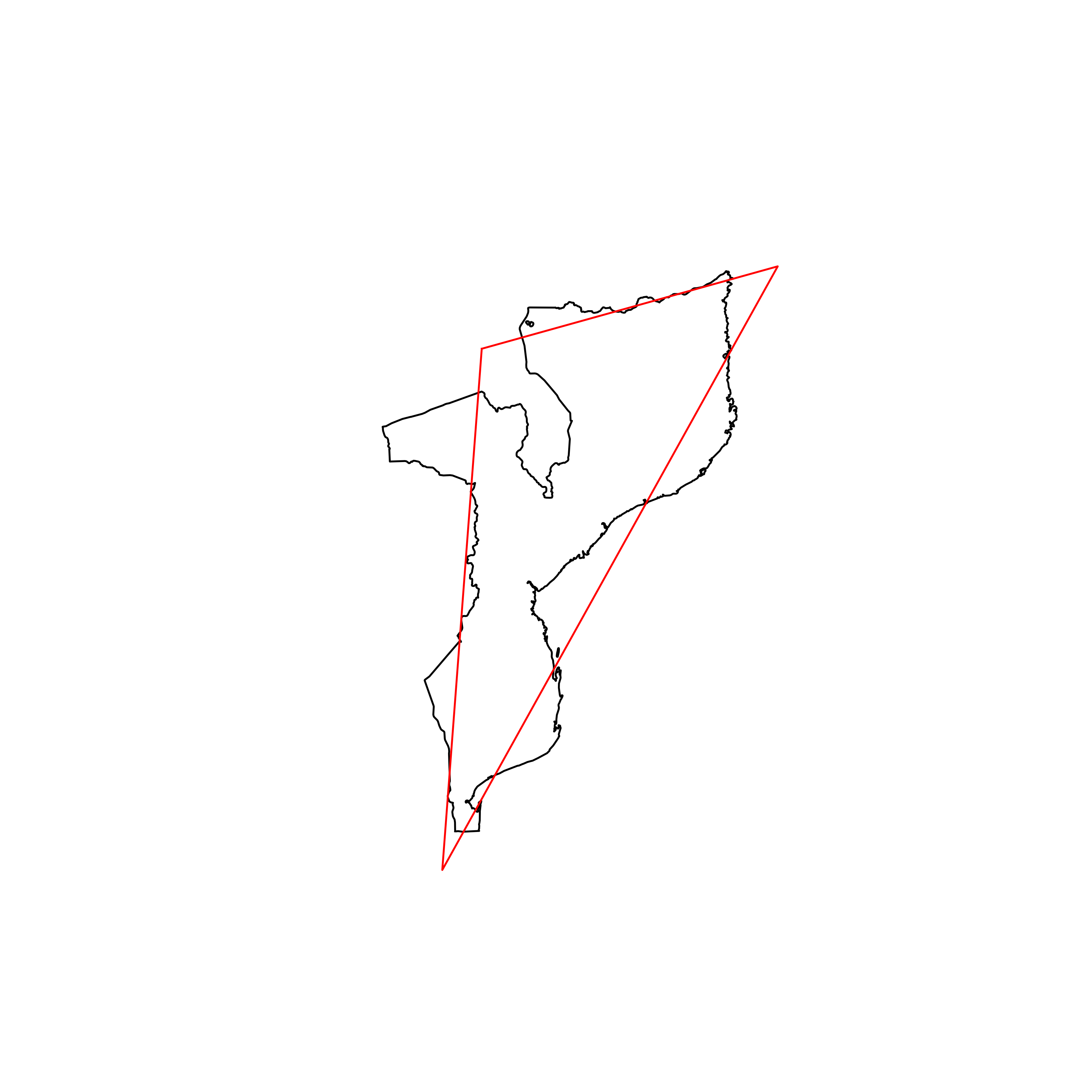 |
| 155 | Tajikistan | 0.785365 | 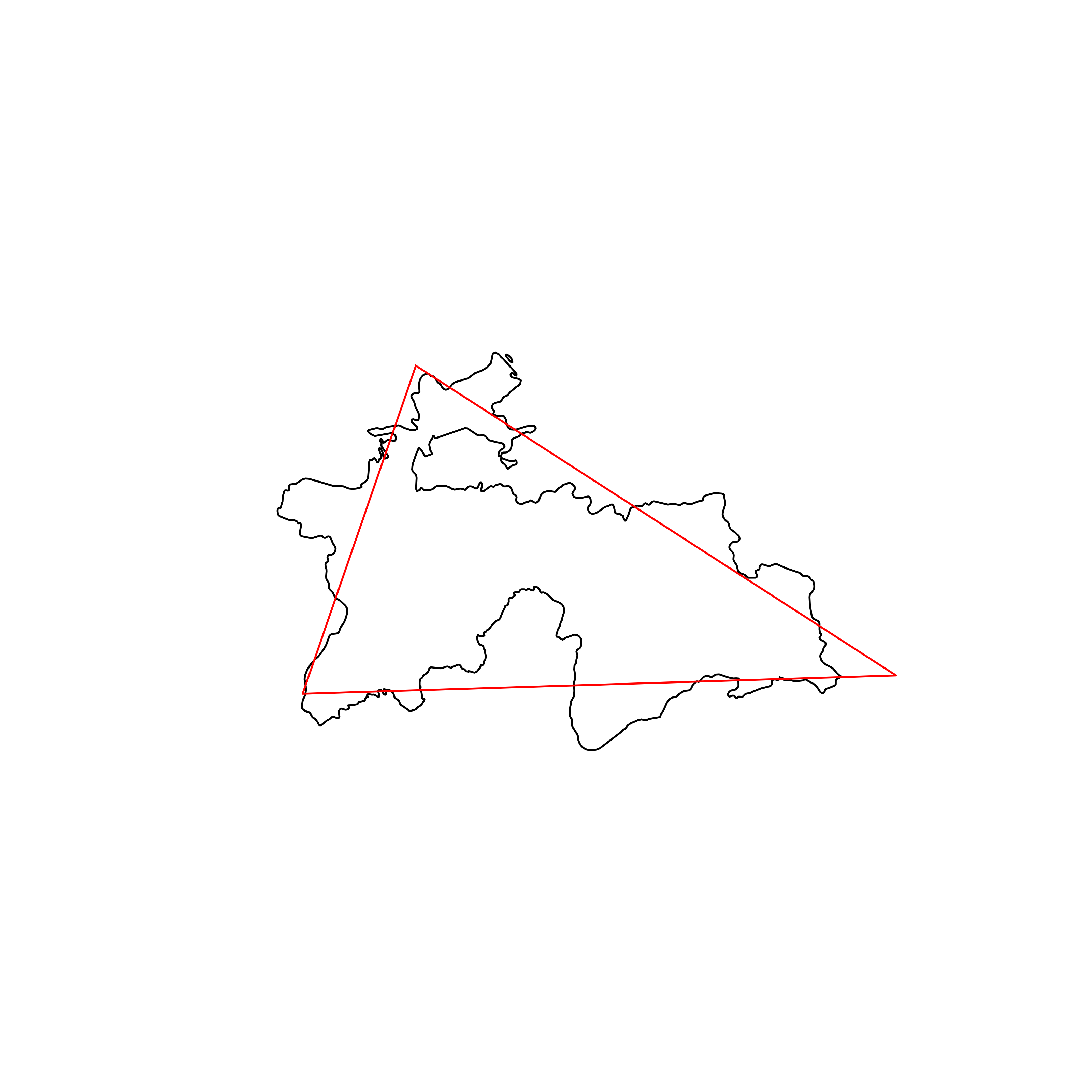 |
| 156 | Laos | 0.781655 | 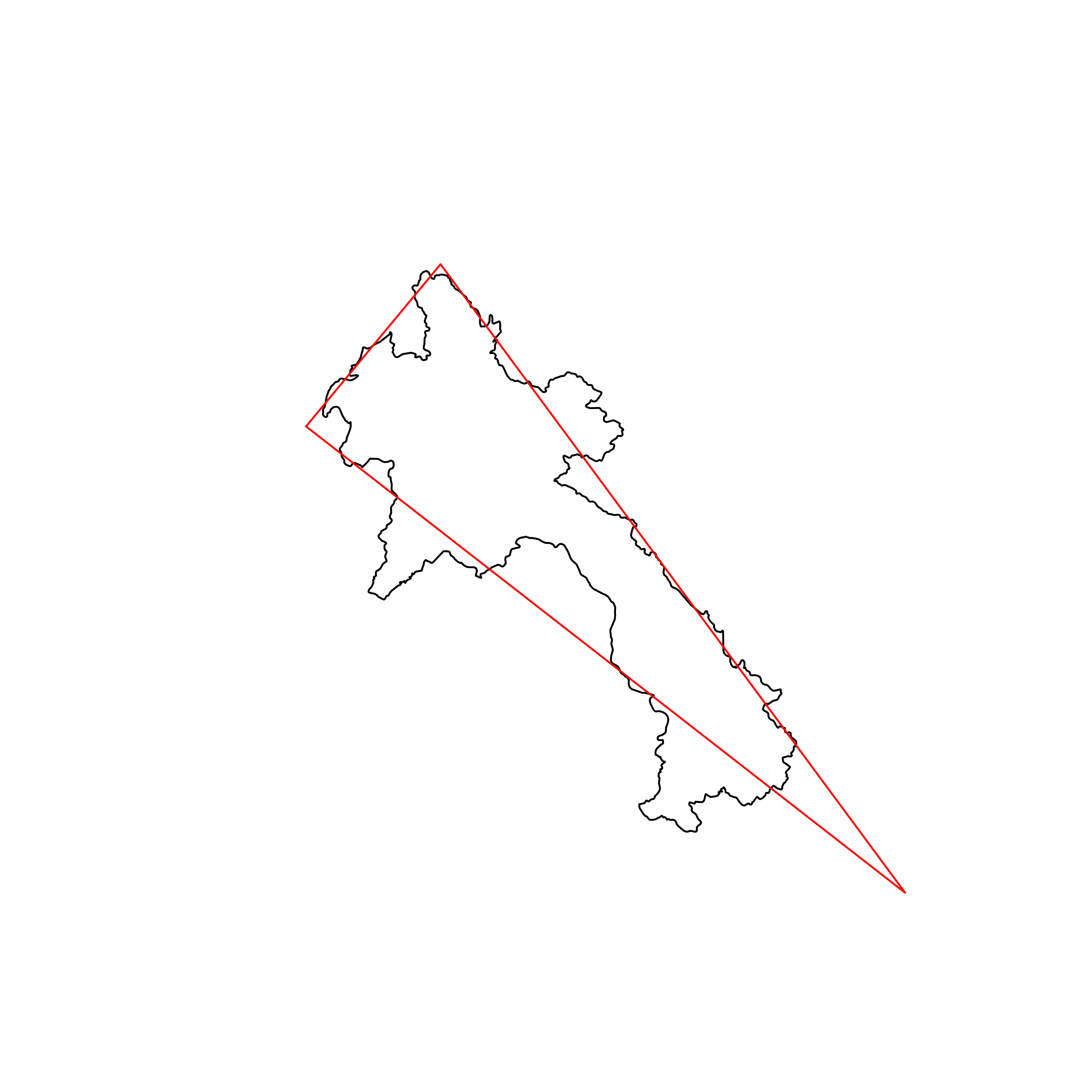 |
| 157 | United States of America | 0.771845 |  |
| 158 | Mexico | 0.762001 | 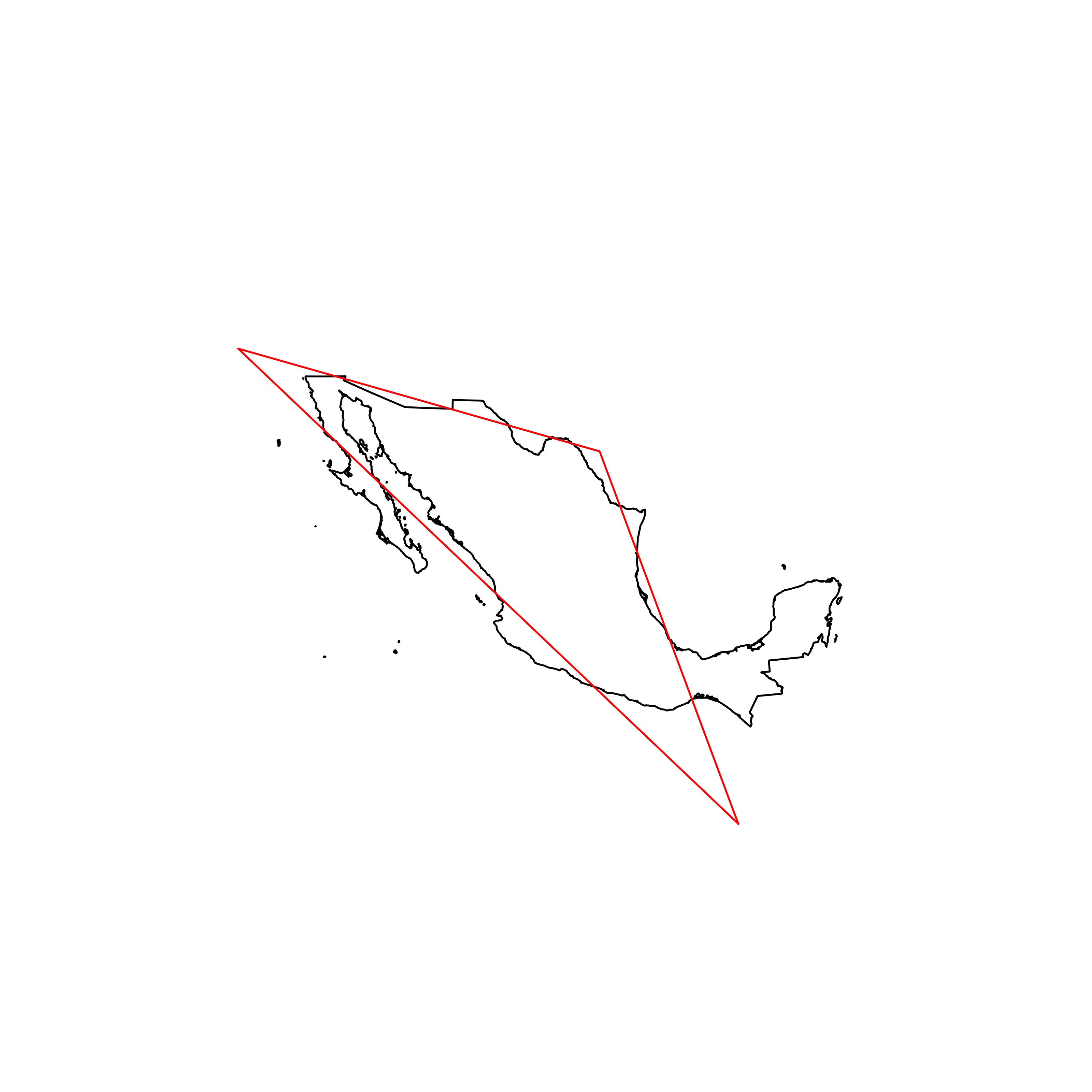 |
| 159 | Israel | 0.758537 | 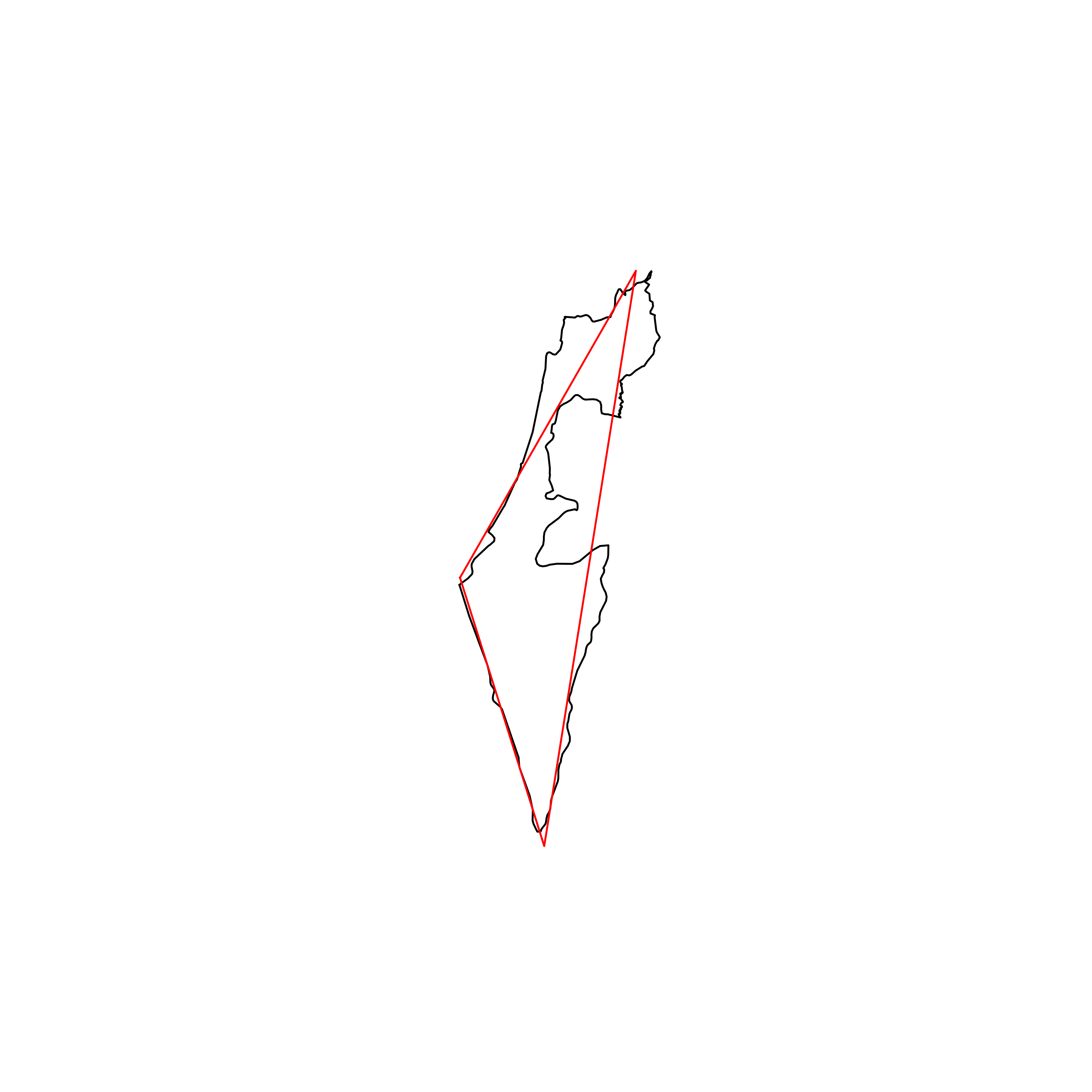 |
| 160 | Brunei | 0.752157 | 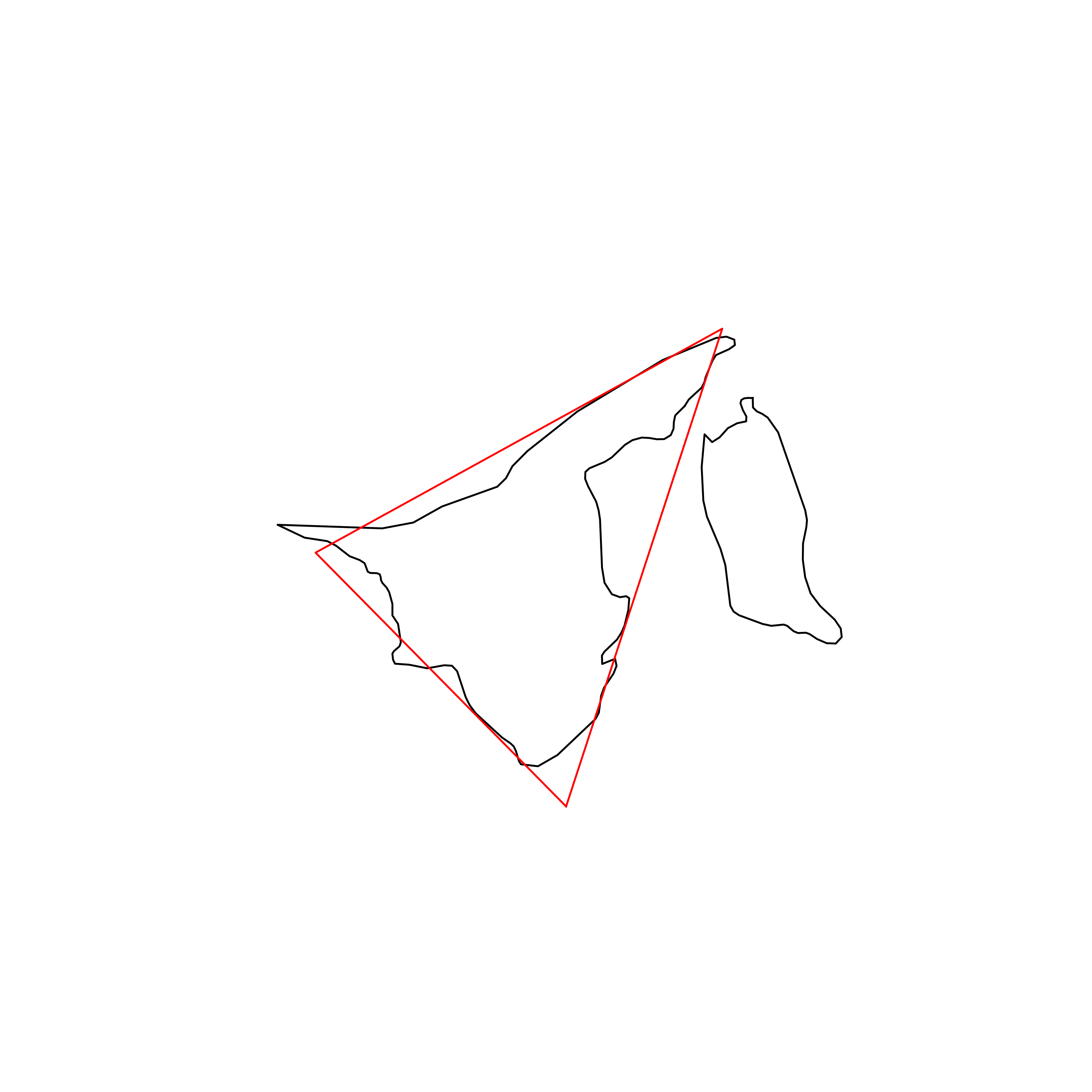 |
| 161 | Papua New Guinea | 0.748362 | 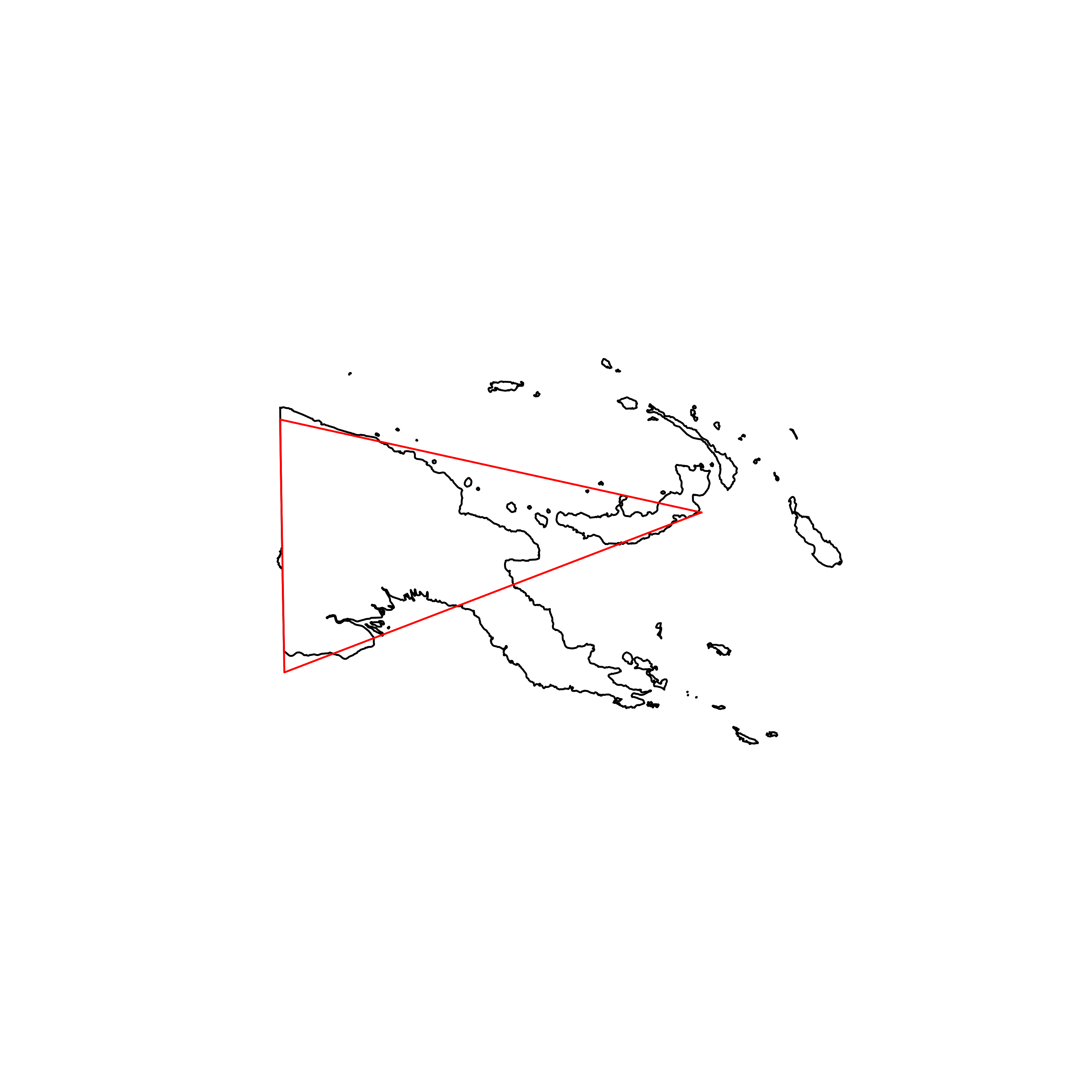 |
| 162 | Canada | 0.747720 | 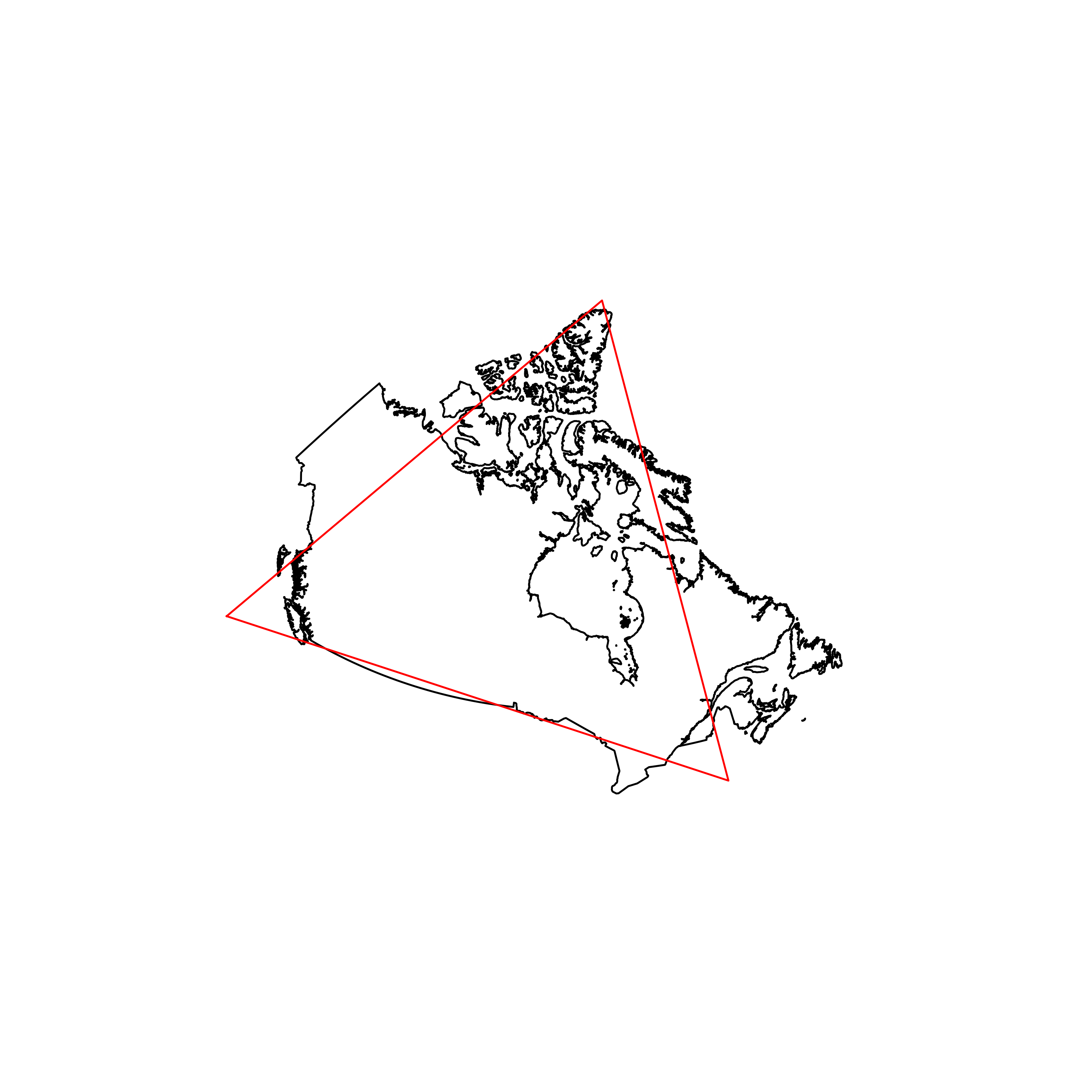 |
| 163 | Cuba | 0.735471 |  |
| 164 | France | 0.734136 |  |
| 165 | Italy | 0.729978 | 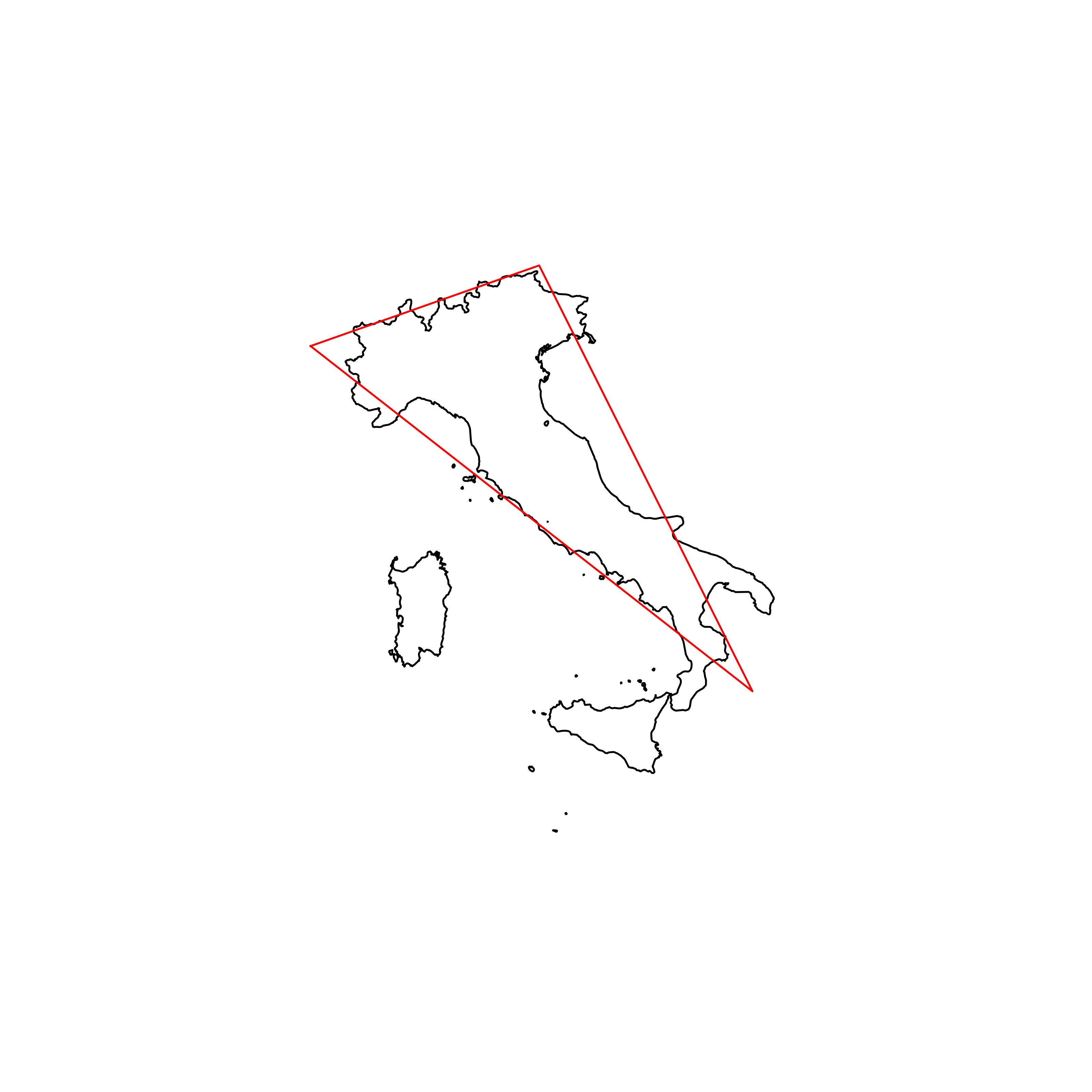 |
| 166 | New Zealand | 0.723253 |  |
| 167 | Samoa | 0.719025 | 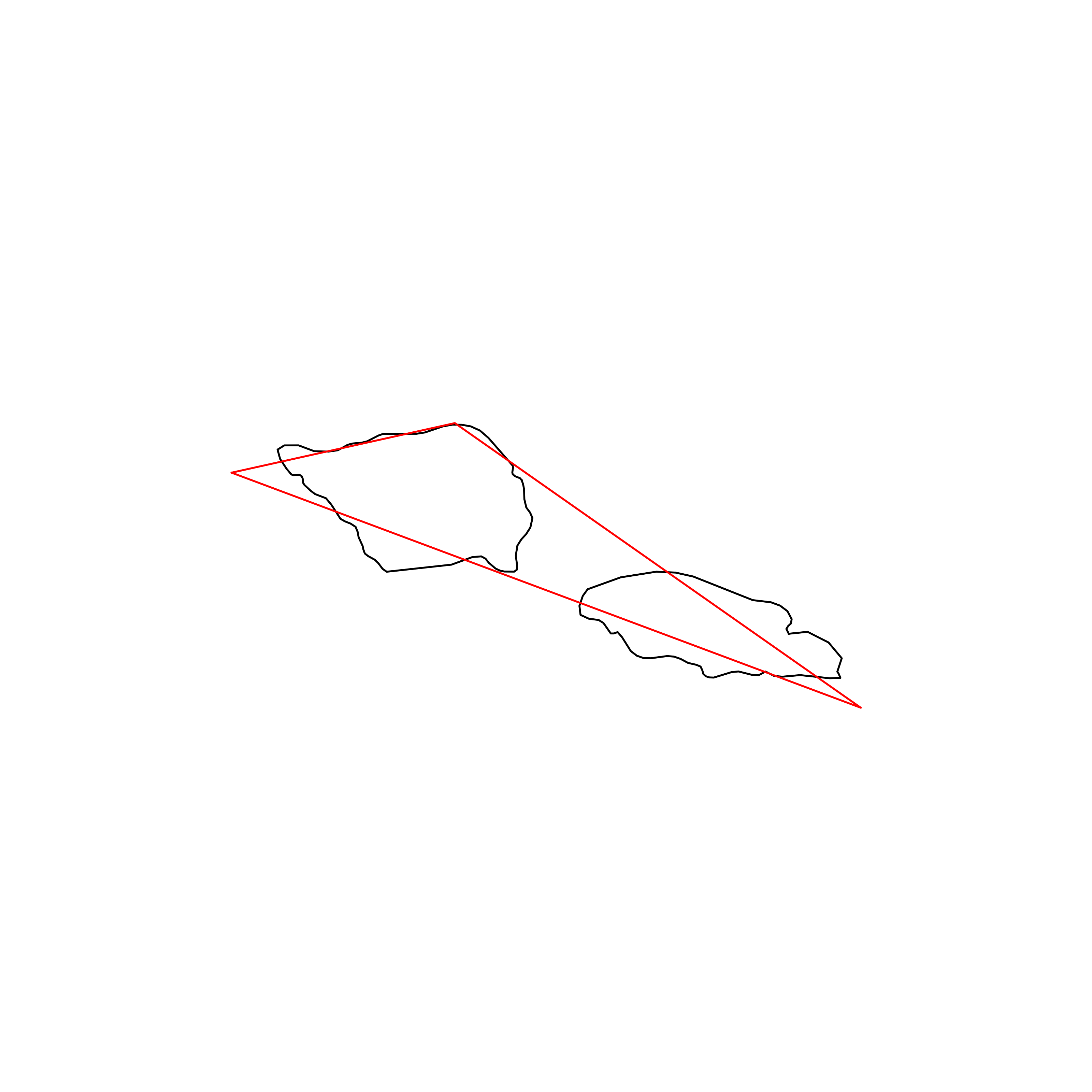 |
| 168 | Greece | 0.710513 | 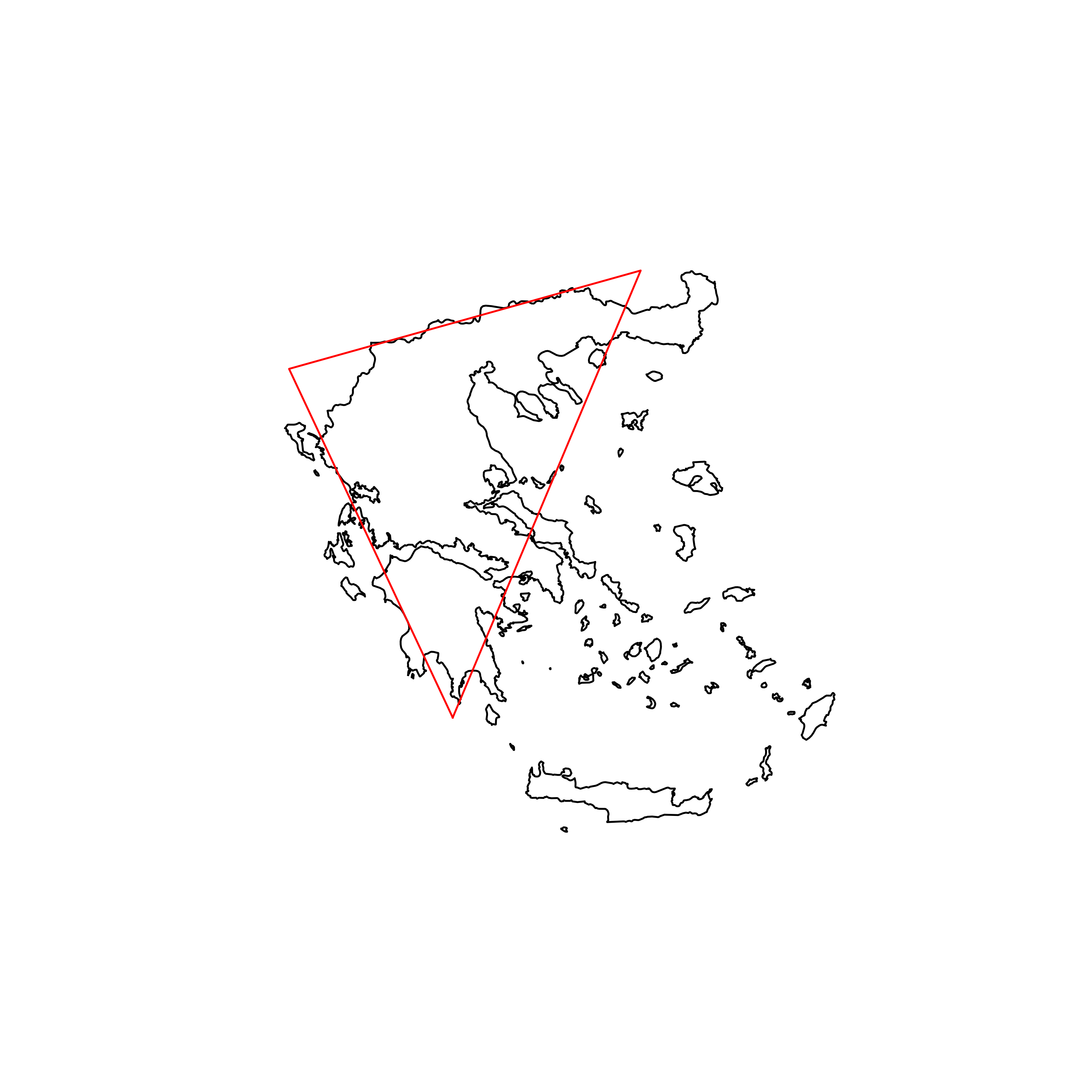 |
| 169 | Haiti | 0.709348 | 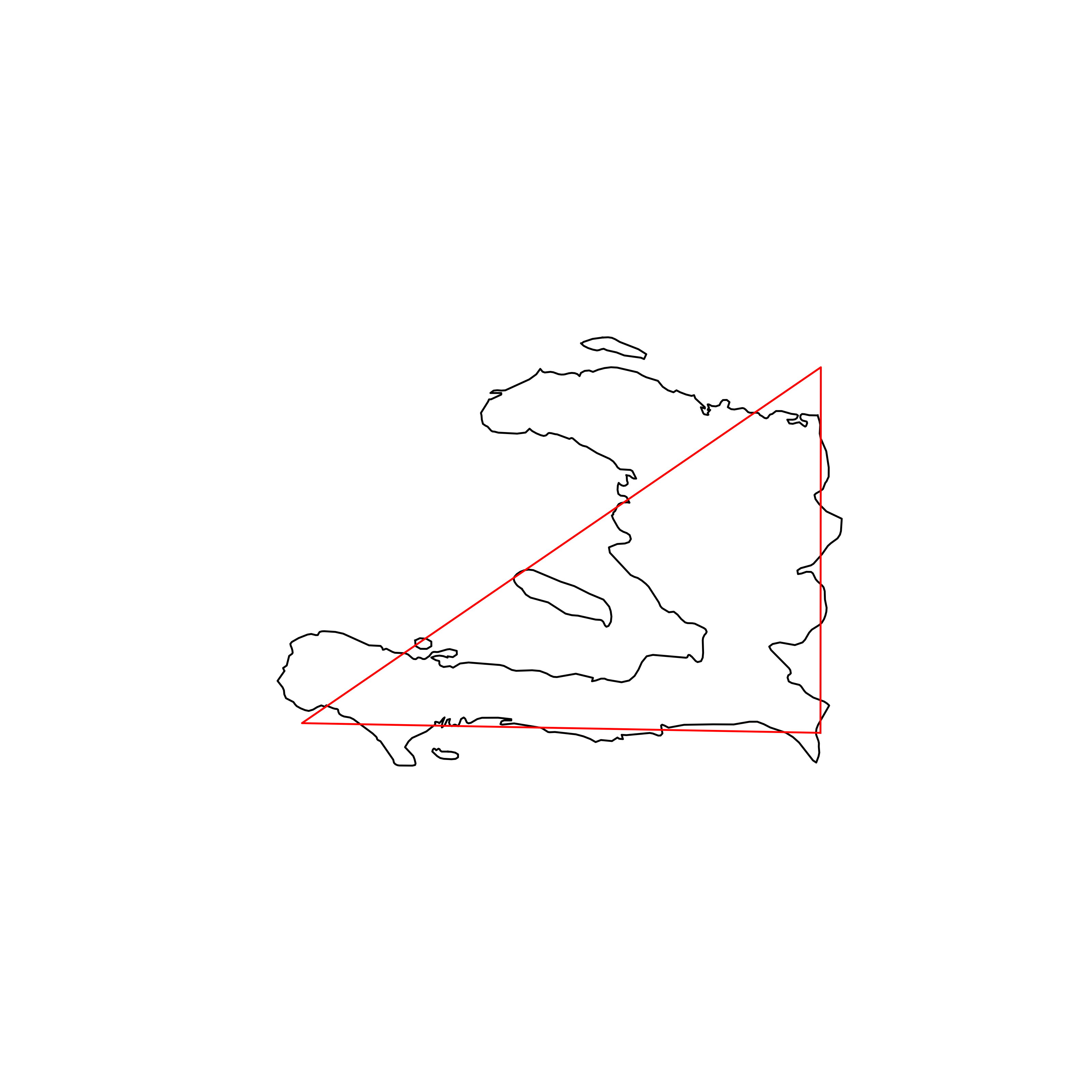 |
| 170 | Gambia | 0.706181 |  |
| 171 | Denmark | 0.702239 | 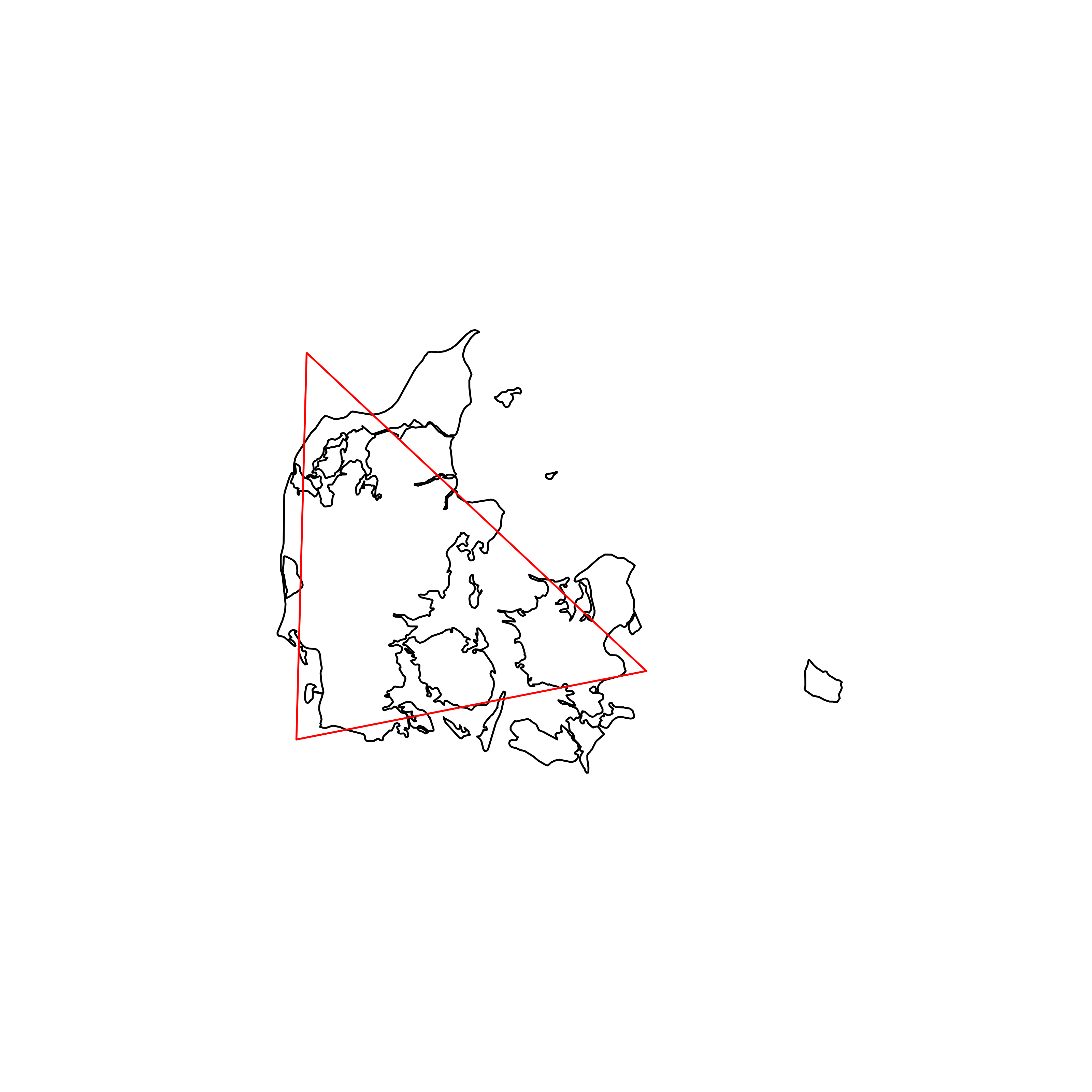 |
| 172 | Chile | 0.694678 |  |
| 173 | Saint Kitts and Nevis | 0.694223 | 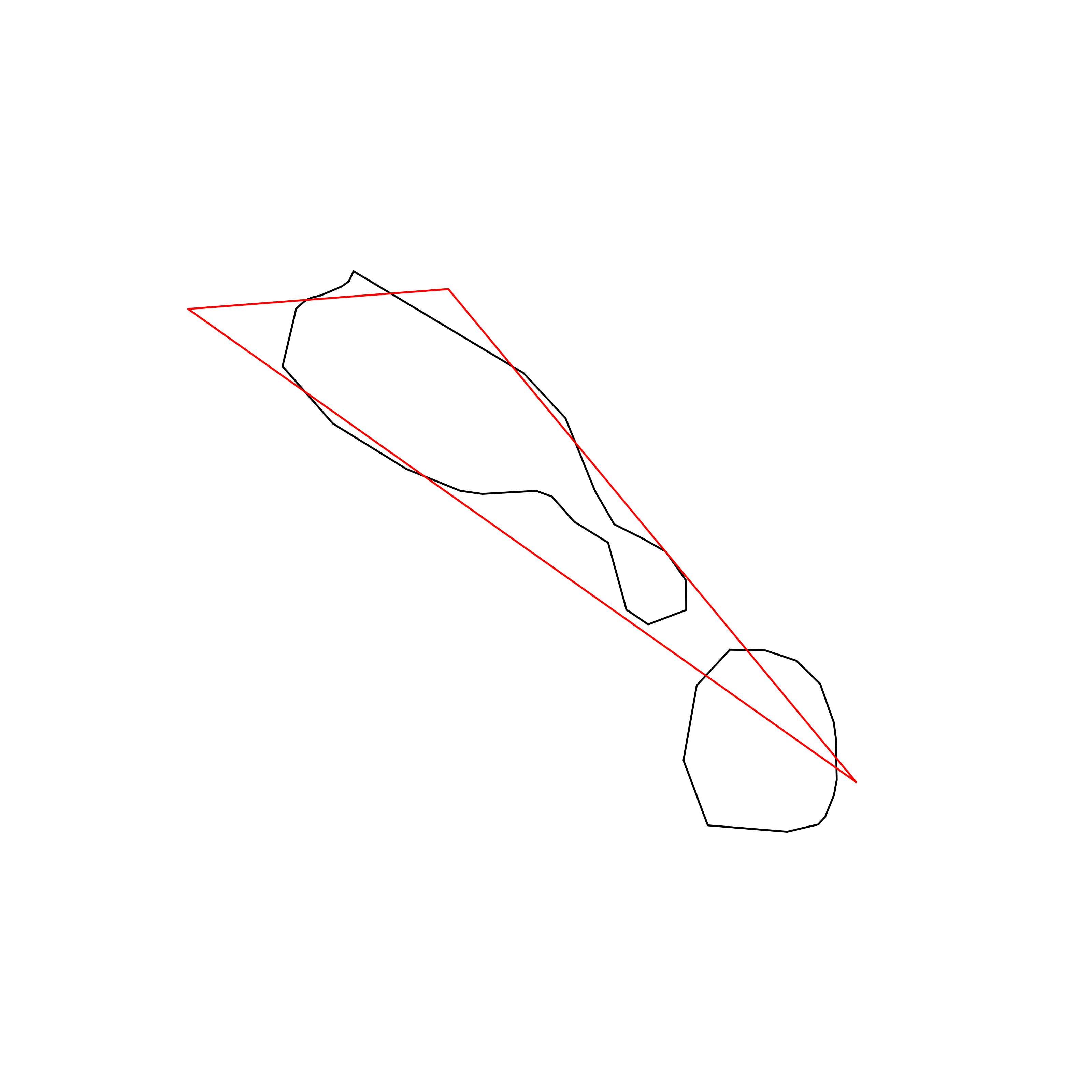 |
| 174 | Palau | 0.685319 |  |
| 175 | Croatia | 0.667609 | 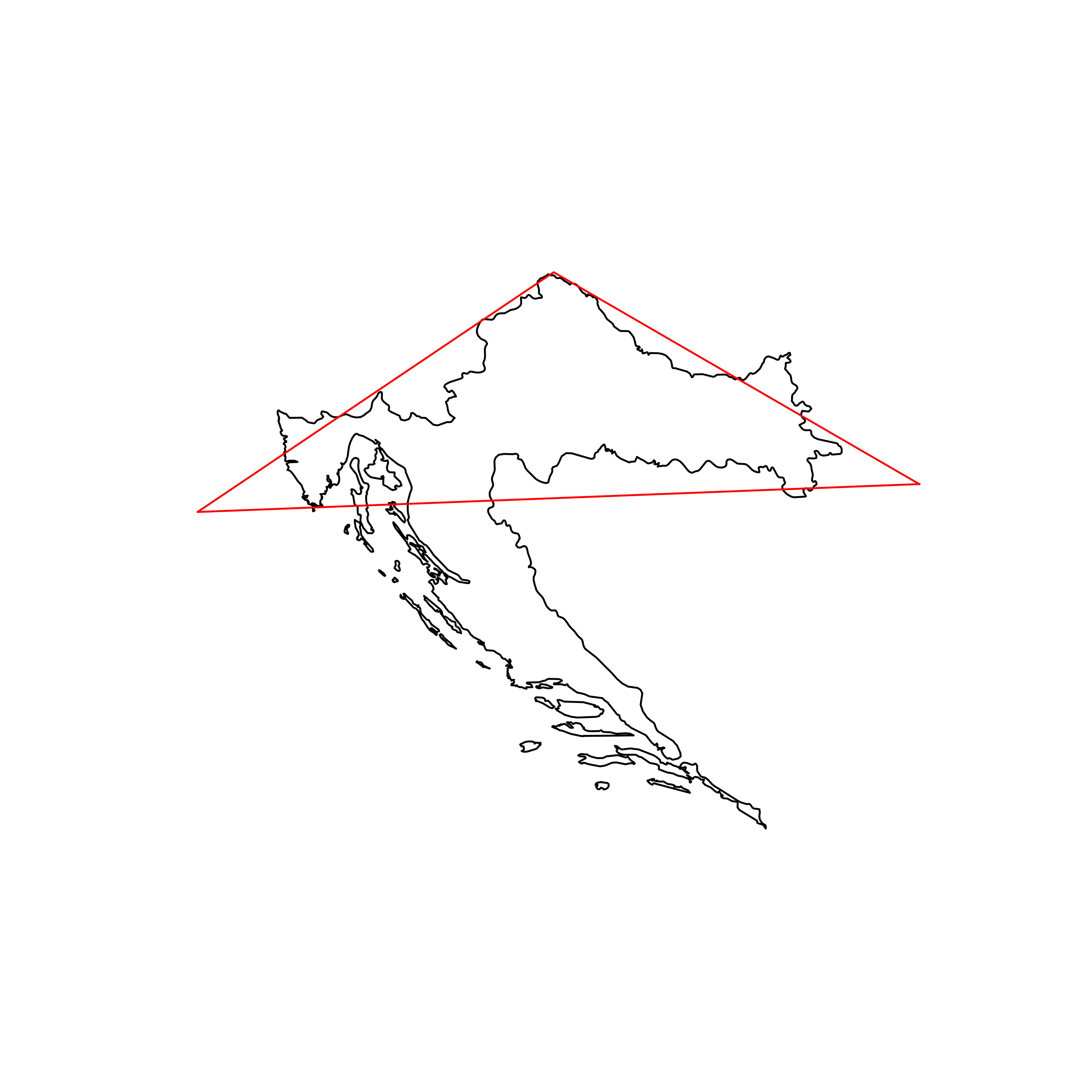 |
| 176 | Panama | 0.650465 | 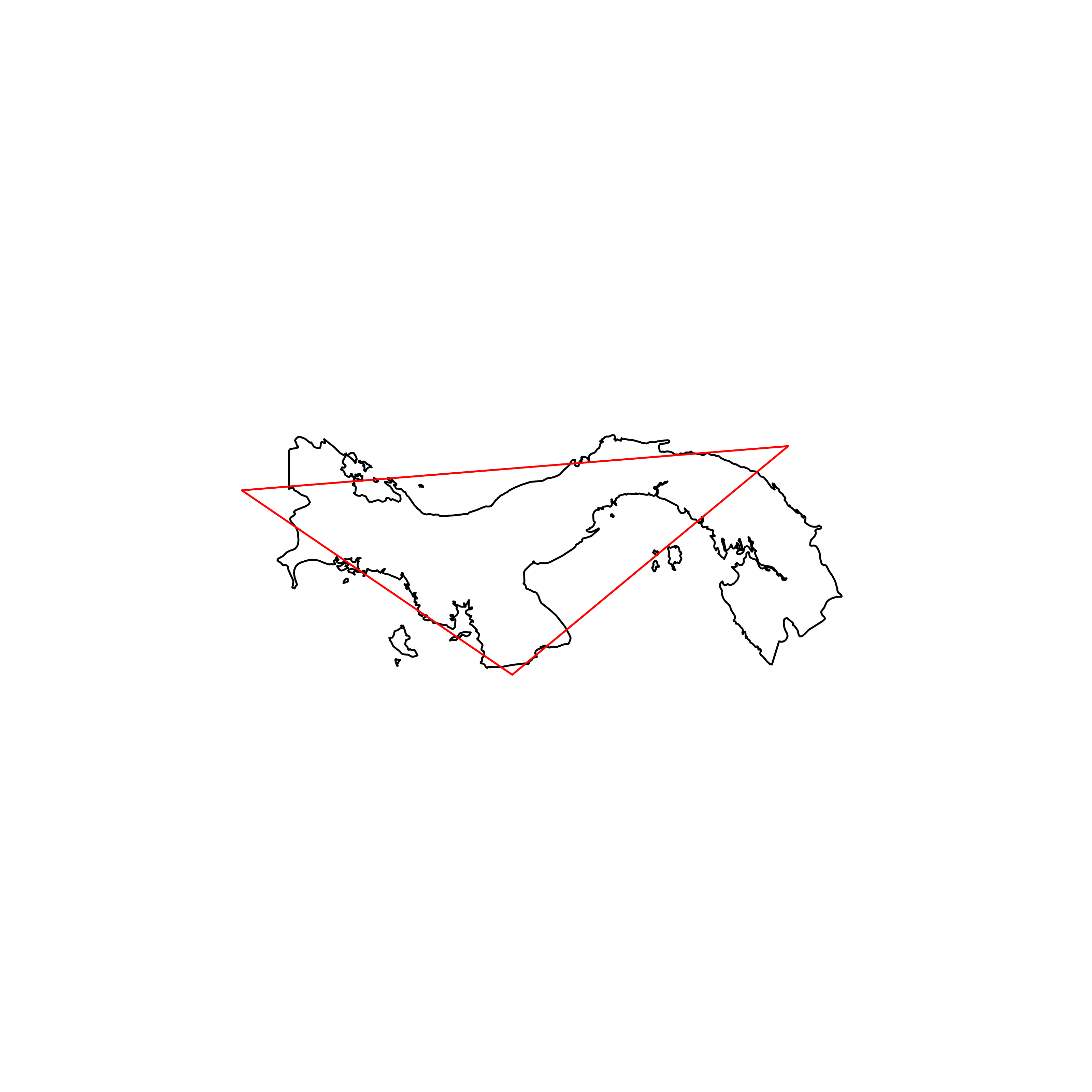 |
| 177 | Japan | 0.649205 | 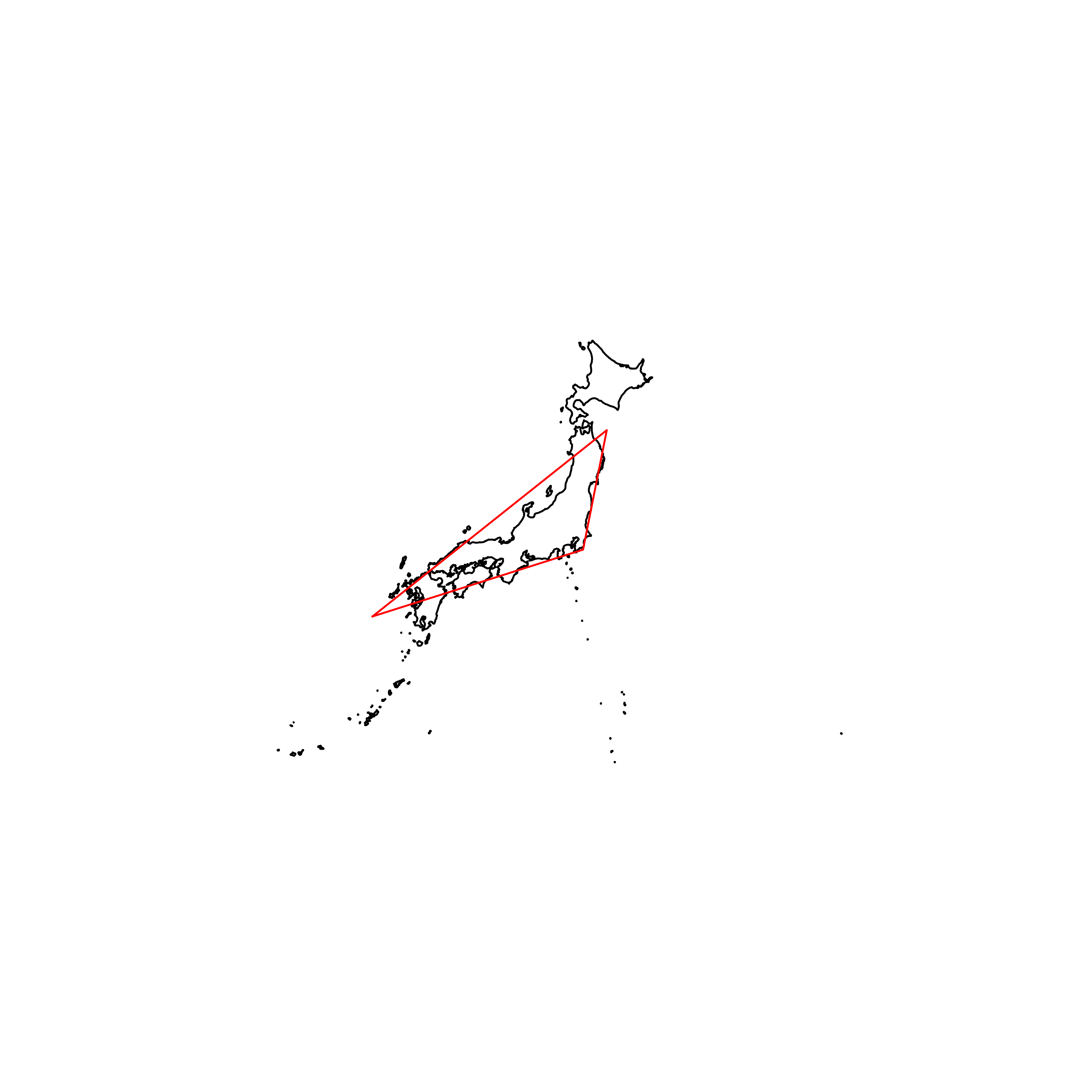 |
| 178 | Fiji | 0.645017 |  |
| 179 | Norway | 0.635156 |  |
| 180 | Vietnam | 0.629038 | 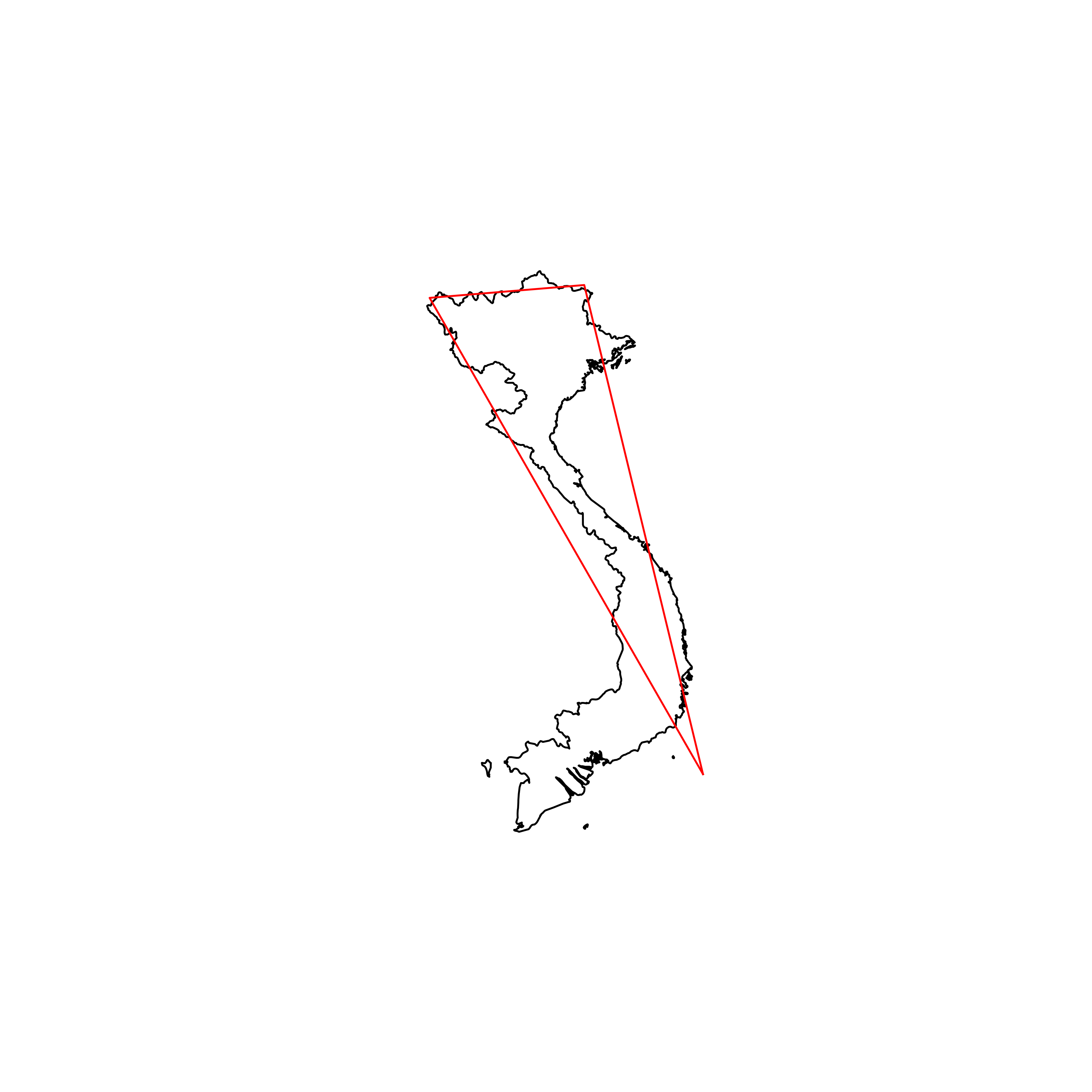 |
| 181 | Antigua and Barbuda | 0.614450 | 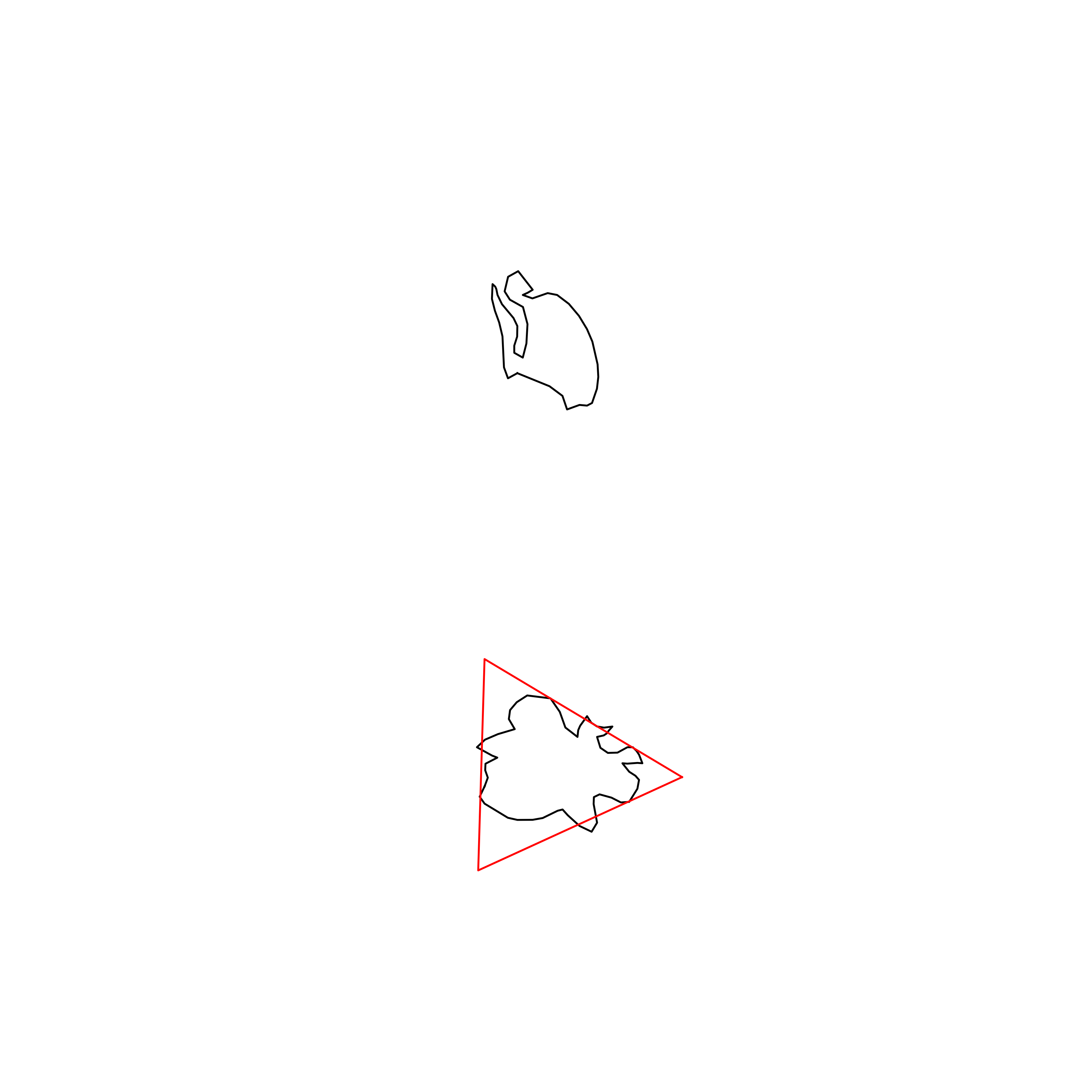 |
| 182 | Comoros | 0.612388 |  |
| 183 | Malaysia | 0.561826 | 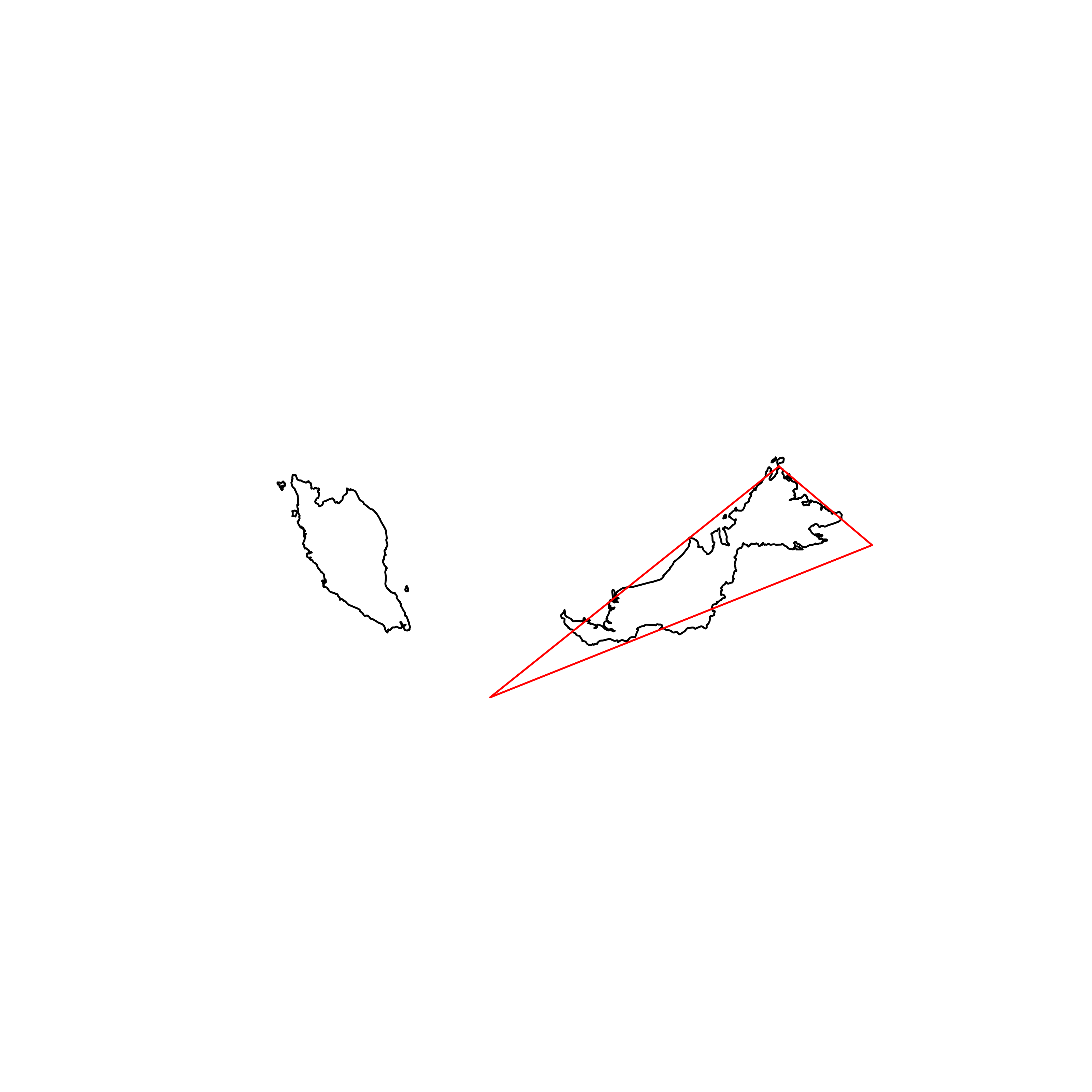 |
| 184 | Federated States of Micronesia | 0.536417 |  |
| 185 | Philippines | 0.536229 | 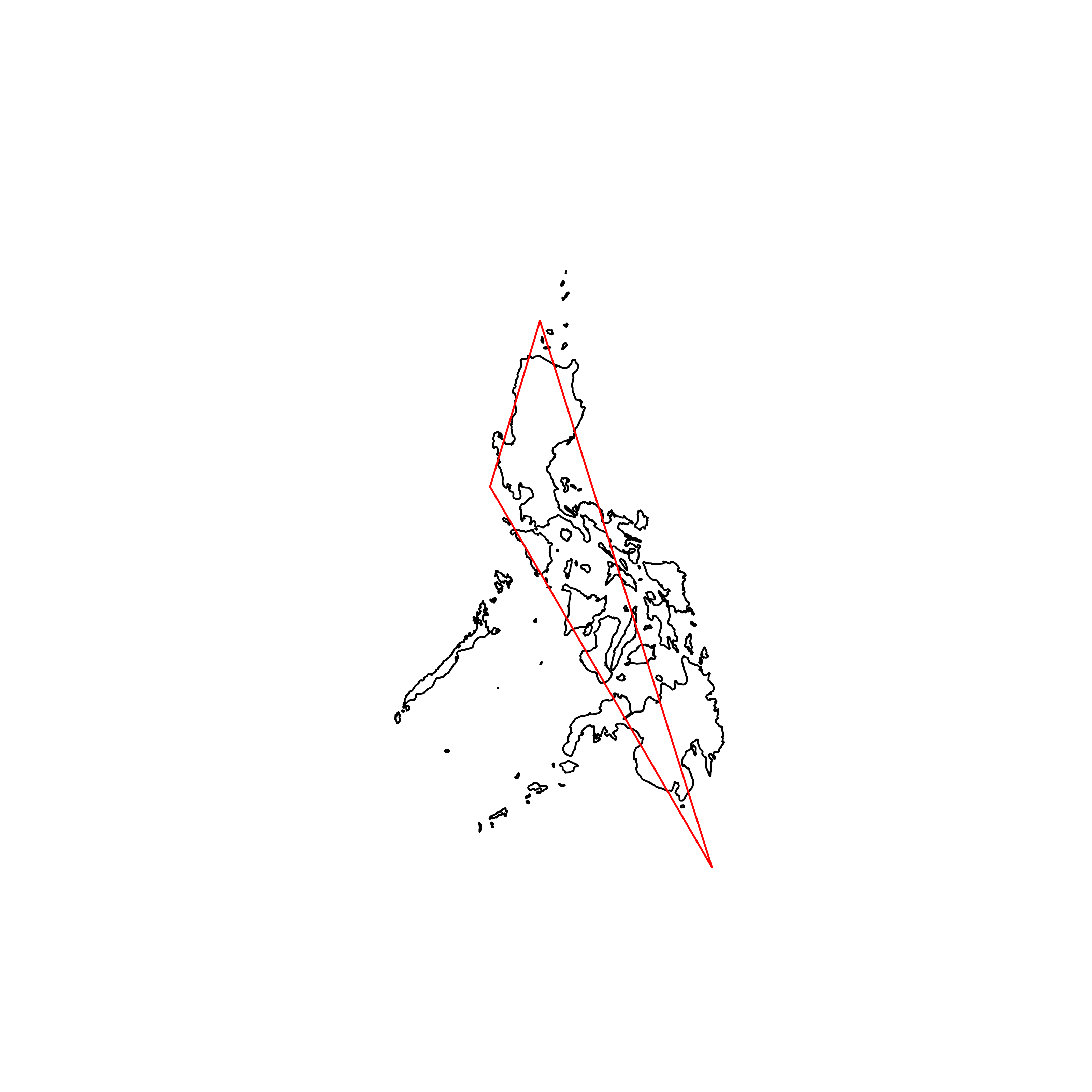 |
| 186 | Indonesia | 0.493143 | 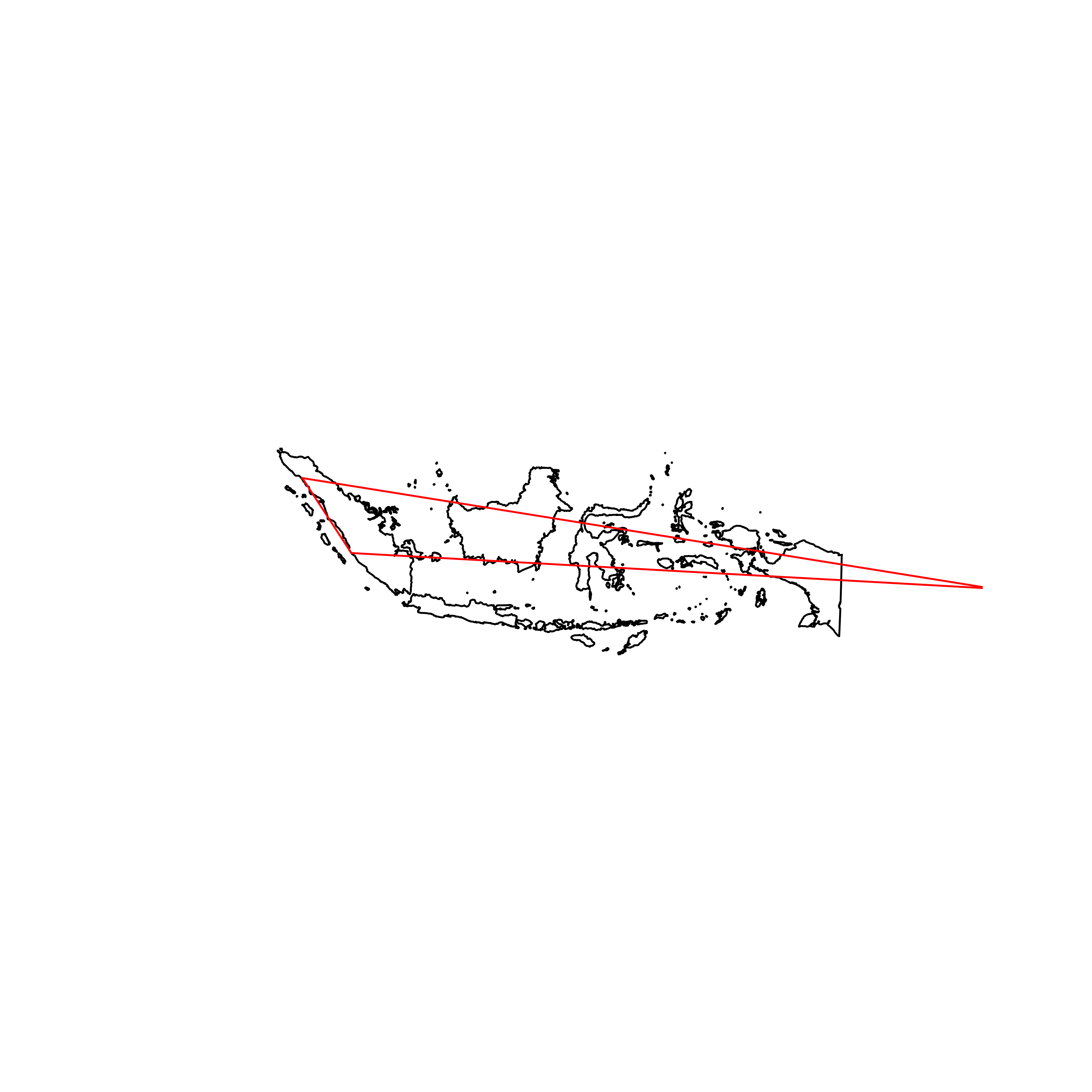 |
| 187 | Vanuatu | 0.473048 | 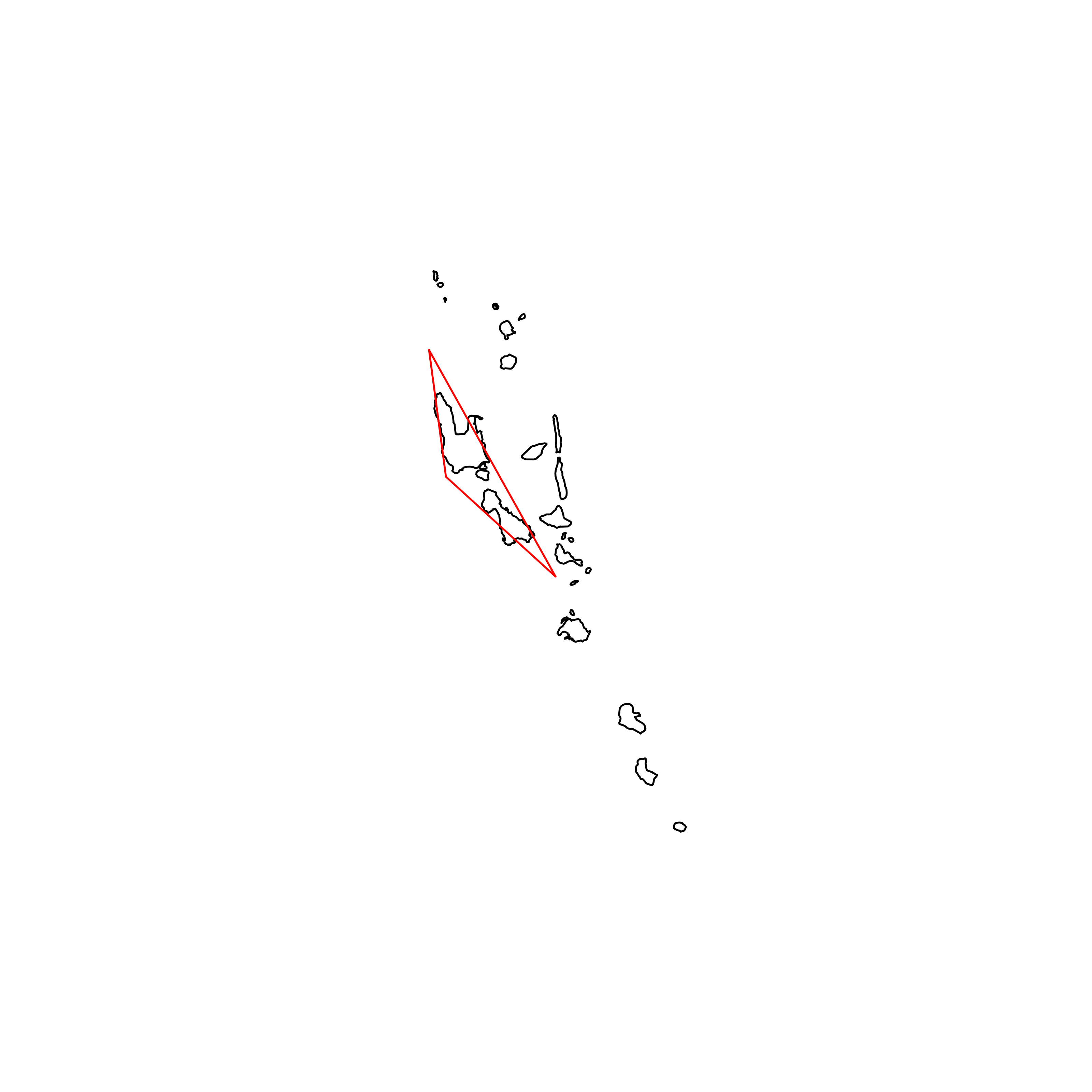 |
| 188 | Tonga | 0.429500 |  |
| 189 | The Bahamas | 0.405978 | 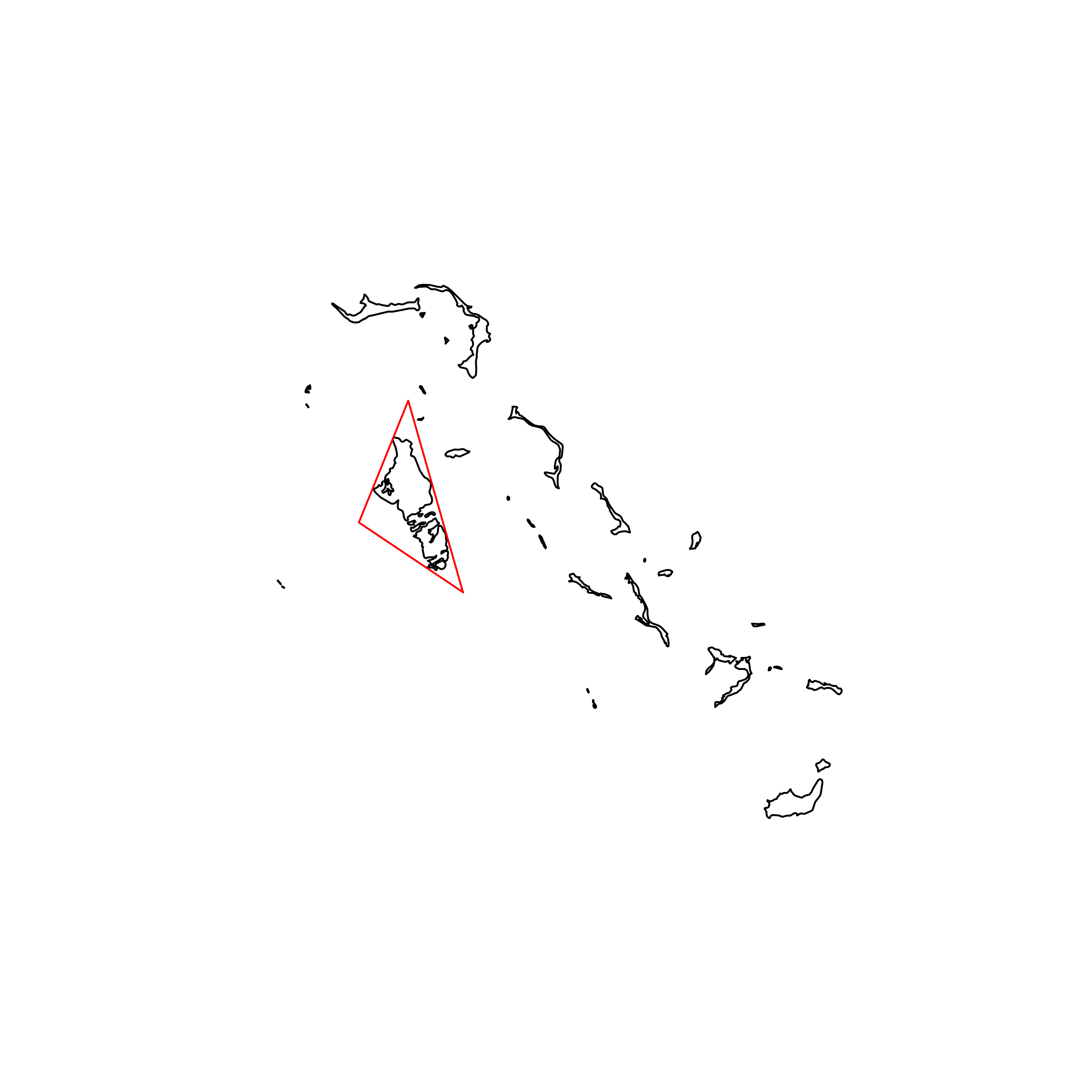 |
| 190 | Seychelles | 0.388652 |  |
| 191 | Solomon Islands | 0.368949 |  |
| 192 | Cabo Verde | 0.309594 | 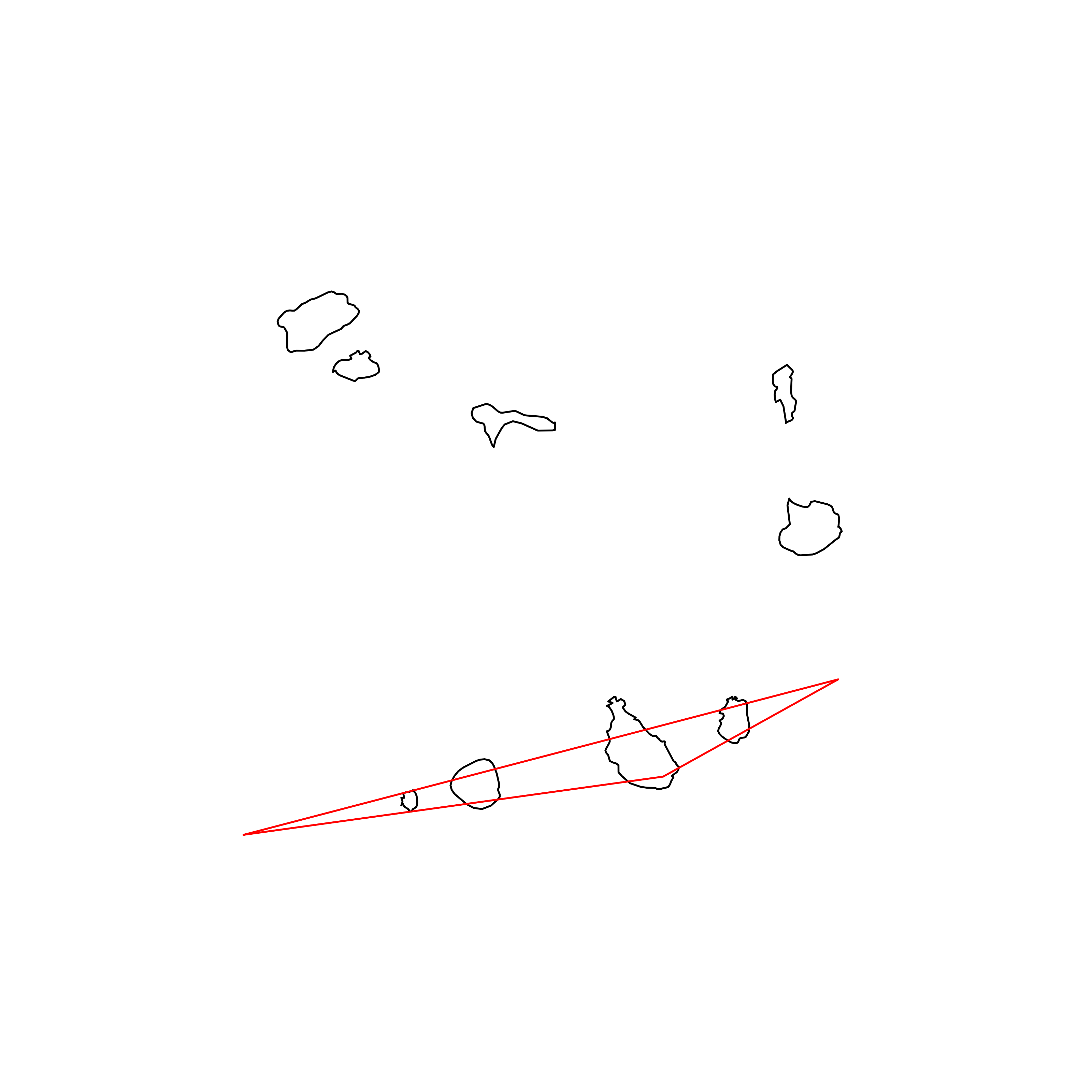 |
| 193 | Maldives | 0.203665 |  |
| 194 | Tuvalu | 0.144069 |  |
| 195 | Kiribati | 0.138684 |  |
| 196 | Marshall Islands | 0.084072 |  |
Code
Python code to calculate the triangularity of every country in Natural Earth’s ne_10m_admin_0_countries.shp shapefile.
import shapefile
import pyproj
import random
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from shapely.geometry import Polygon
from shapely.strtree import STRtree
from scipy.optimize import minimize
def transform_points(points):
"""
converts from lat lon to azimuthal projection on center of points - returns converted points
(adapted from https://gciruelos.com/what-is-the-roundest-country.html)
"""
xs = [x for x,_ in points]
ys = [y for _,y in points]
lon = np.mean(xs)
lat = np.mean(ys)
FROM_PROJ = '+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs'
to_proj = '+proj=aeqd +R=6371000 +lat_0=%.2f +lon_0=%.2f ' \
'+no_defs' % (lat, lon)
tpoints = [pyproj.transform(pyproj.Proj(FROM_PROJ),pyproj.Proj(to_proj),x,y)
for x,y in points]
return tpoints
def get_polys(points, parts):
""" - returns polygons from points and parts
"""
polys = []
for j,k in enumerate(parts):
if j == len(parts)-1:
poly = Polygon(points[k:])
else:
k_add1 = parts[j+1]
poly = Polygon(points[k:k_add1])
polys.append(poly)
return polys
def similarity(triangle, polys):
""" - returns similarity for given triangle (polygon) and polygons (country)
"""
# create an STR tree from polygons and find which polygons intersect the triangle
tree_polys = STRtree(polys)
intersecting_polys = tree_polys.query(triangle)
country_area = sum([poly.area for poly in polys])
triangle_area = triangle.area
intersection_area = sum([poly.intersection(triangle).area for poly in intersecting_polys])
sim = intersection_area / max(triangle_area, country_area)
return sim
def run_simplex(x0, polys):
"""
maximise triangularity for a set of polygons (country) using Nelder-Mead method
given initial guess x0
where first 3 elements of x0 are coordinates [x1,x2,x3] and last three elements are [y1,y2,y3] - returns an OptimizeResult object (see https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html#scipy.optimize.OptimizeResult)
"""
def cost_function(x):
triangle = Polygon((x[i],x[i+3]) for i in range(3))
cost = 1 - similarity(triangle, polys)
return cost
# minimize cost function (1 - triangularity) to find best triangle
res = minimize(cost_function, x0, method = "Nelder-Mead")
return res
def run_trials(n, polys, points):
"""
runs optimisation routine n times with randomised initial guesses (random three points on country's border) - returns best triangularity found, and corresponging triangle (polygon)
"""
best_triangularity = 0
# run with n times with different initial guesses
for i in range(n):
# the initial guess first 3 are x-coords, last 3 are y-coords
rand_points = random.sample(set(points), 3)
x0 = [point[0] for point in rand_points] + [point[1] for point in rand_points]
res = run_simplex(x0, polys)
triangularity = 1 - res["fun"]
print(triangularity)
x = res["x"]
if triangularity >= best_triangularity:
best_triangularity = triangularity
best_x = x
triangle = Polygon((best_x[i],best_x[i+3]) for i in range(3))
return best_triangularity, triangle
def main():
"""
main function runs through all countries in shape file
finds optimal triangularity after n runs of optimisation routine per country - saves corresponding trianglularity per country in a CSV file - saves plot of each country with optimal triangle
"""
# PARAMETERS
# input shape file data
input_data = "country//ne_10m_admin_0_countries.shp"
# number of times optimisation routine is run per country (with different initial guess)
n = 20
# read shape file and get shapes
sf = shapefile.Reader(input_data)
shapes = sf.shapes()
# list of countries
countries = [sf.record(i)[8] for i in range(len(shapes))]
num_countries = len(countries)
opt_triangularities = []
for i, country in enumerate(countries):
try:
print("(" + str(i+1) + "/" + str(num_countries) + ") " + country)
s = shapes[i]
# get (transformed points) and parts of country
tpoints = transform_points(s.points)
parts = s.parts
# get polygons of country
polys = get_polys(tpoints, parts)
# optimisation
xs = [x for x,_ in tpoints]
ys = [y for _,y in tpoints]
min_xs = min(xs)
max_xs = max(xs)
min_ys = min(ys)
max_ys = max(ys)
print("Optimising...")
triangularity, triangle = run_trials(n, polys, tpoints)
opt_triangularities.append(triangularity)
print("Triangularity: " + str(triangularity))
# set up figure for plotting
fig, ax = plt.subplots(figsize = (8,8))
ys_range = max_ys - min_ys
xs_range = max_xs - min_xs
plot_range = max(xs_range, ys_range)
xs_center = np.mean((min_xs, max_xs))
ys_center = np.mean((min_ys, max_ys))
ax.set_xlim(xs_center-0.75*plot_range, xs_center+0.75*plot_range)
ax.set_ylim(ys_center-0.75*plot_range, ys_center+0.75*plot_range)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.get_xaxis().set_ticks([])
ax.get_yaxis().set_ticks([])
# plot the country
for poly in polys:
plt.plot(*poly.exterior.xy, color="black", linewidth=1)
# plot triangle
plt.plot(*triangle.exterior.xy, color="red", linewidth=1)
plt.savefig(country + ".png", dpi=400)
plt.close('all')
print("\n")
except:
opt_triangularities.append(np.nan)
print("\n")
# make dataframe and save results
df_result = pd.DataFrame({"Country": countries,
"Triangularity": opt_triangularities})
df_result = df_result.sort_values(["Triangularity"], ascending = False)
df_result["Rank"] = np.arange(1,num_countries+1)
df_result = df_result.set_index("Rank")
df_result.to_csv("result.csv")
print("Results Saved")
print("Finished")
if __name__ == "__main__":
main()